离散数学-图的运算与基本概念、导出子图、路与连通

离散数学复习命题公式的范式

离散数学平面图对偶图和着色问题

离散数学谓词逻辑

离散数学-图的运算与基本概念、导出子图、路与连通

离散数学关系的基本运算和关系的性质闭包

离散数学-欧拉图和哈密顿图

图的定义与记号

概念：
简单图
多重图
完全图


平凡图的定义：
1.仅有一个结点的图的称平凡图；
2.平凡图是平凡树；
3.边的集合为空的图叫做零图，1阶零图叫做平凡图，所谓n阶图是指有n个顶点的图；
4.顶点的集合为空的图叫做空图。
零图：只有结点没有边的图。（零图可以多个结点，平凡图只有一个结点）
平凡图是连通图、欧拉图、哈密顿图。
由孤立点组成的图叫做零图，由一个孤立点组成的图叫做平凡图，因而平凡图一定是零图。
全关系-恒等关系：完全图
空关系：零图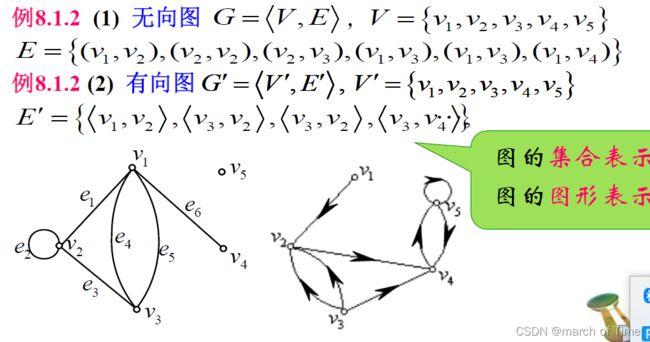

邻接矩阵

关联矩阵

设G=V,E是无向图，其中V={v1,v2,…,vn},将n×m阶矩阵×称为G的关联矩阵，记为M(G)。其中元素表示结点v与边e的关联次数，如下所示

设D=V,E是有向图，其中V={v1,v2,…,vn},将n×m阶矩阵×称为D的关联矩阵，记为M(D)。其中元素表示结点v与边e的关联情况，如下所示：




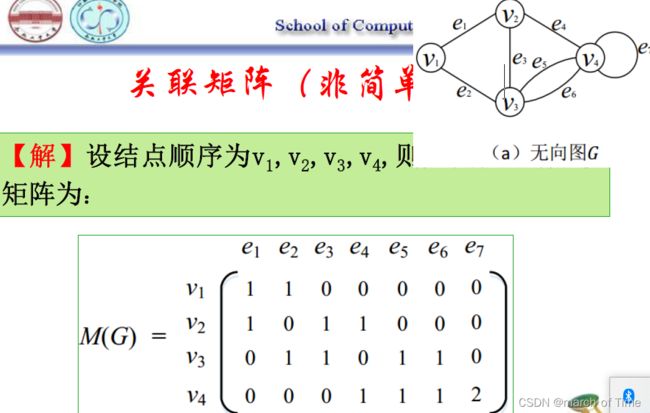
[结论]
（1）对于无向图及其关联矩阵，由于每条非自环边关联2个结点，故矩阵中每列元素之和必为2。
（2）对于有向图及其关联矩阵，由于每条非自环有向边关联2个结点，且一个为起点一个为终点，故图中每个非自环边在关联矩阵中所对应列元素之和必为0.

 当图模型中的边数较多时，邻接矩阵和关联矩阵比较有效。
 当图模型中的边数较少时，邻接矩阵和关联矩阵的的表示方法比较浪费资源，可用邻接表的方法表示图模型。

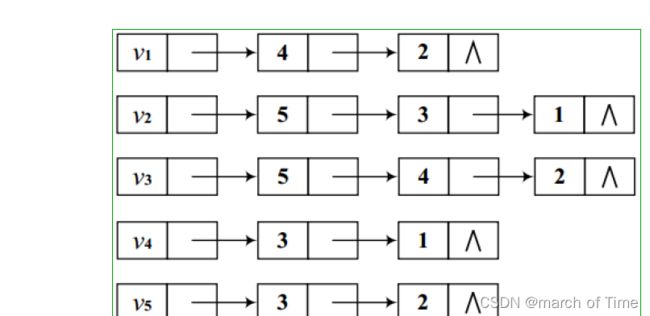
邻接表

邻接表
⨠⨠邻接表主要是分别对图G=V,E中每个结点建立一个单链表。
⨠⨠对于结点的单链表，该表的第一个存储单元为表头，存放结点的有关信息，表中其它存储单元存放与所有结点相关联边的信息

图的运算和算法

集合运算：
假设1=1,1和2=2,2是任意给定的图模型，则有：
(1)如果1∩2=∅，则称1和2是不交的；
(2)如果1∩2=∅，则称1和2是边不交的，或者说是不重的。

设G1=和G2=都是不含孤立结点的图(同为无向图或有向图)。
⨠⨠由G1和G2中所有边与结点组成的图称为G1和G2的(union)，记作G1∪G2。其中V=V1 ∪ V2 , E=E1 ∪ E2。当 G1和G2不存在公共边时，称G1∪G2为G1和G2的不重并。
⨠⨠由G1和G2的公共边组成的图称为G1和G2的交(cap)，记作G1∩G2。其中V=V1 ∩ V2 , E=E1 ∩ E2。
仅由G1中去掉G2中的边组成的图称为G1和G2的差 (difference)，
记作G1-G2。其中V=V1, E=E1 -E2
在G1和G2的并中去掉G1和G2的交所得到的图称为G1和G2的环和 记作

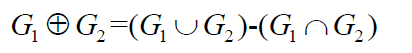
(1) 若=，则∩=∪=()， −=−=∅。
(2) 与不交时，∩=∅，−=， −=，⊕=∪。
(3) ⊕=∪−（∩）

修改运算：

例子：

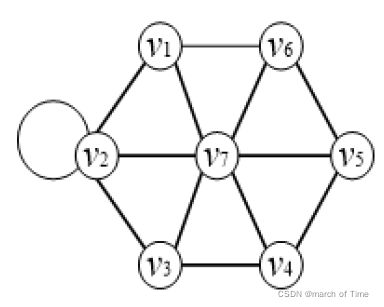
•图 (b)表示−(,)；
•图 ©表示−{,,,,,,(,)}；
•图 (d)表示 −；
•图 (e)表示−{,,,}；
•图 (f)表示(,)；
•图 (g)表示∪(,)；
•图 (h)表示∪((,)。

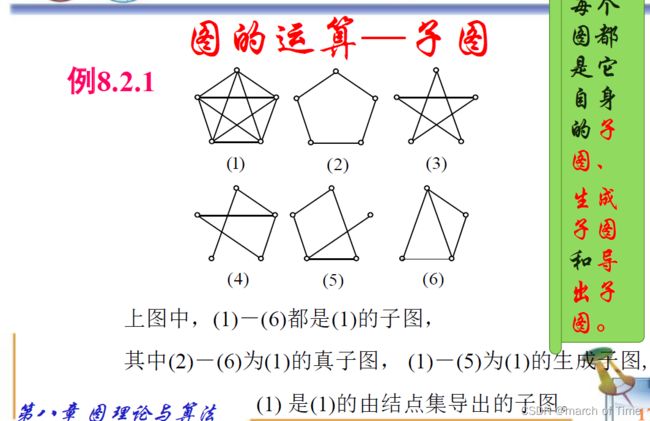
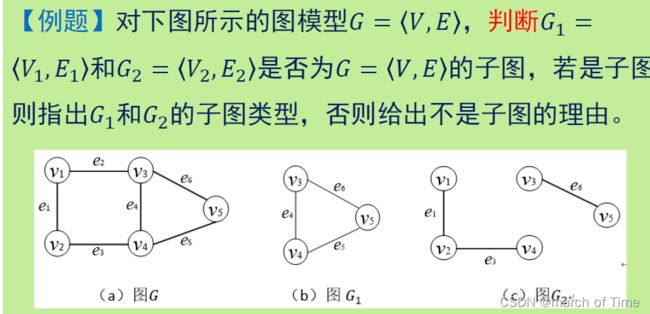
图的运算–子图

补图：

图的度

各顶点的度均相同的图称为正则图(regular graph),各顶点度均为k的正则图称为k-正则图。
8.2.10.对于图G = ，度数为1的结点称为悬挂结点(Hanging Point)，以悬挂结点为端点的边称为悬挂边(Hanging Edge)。

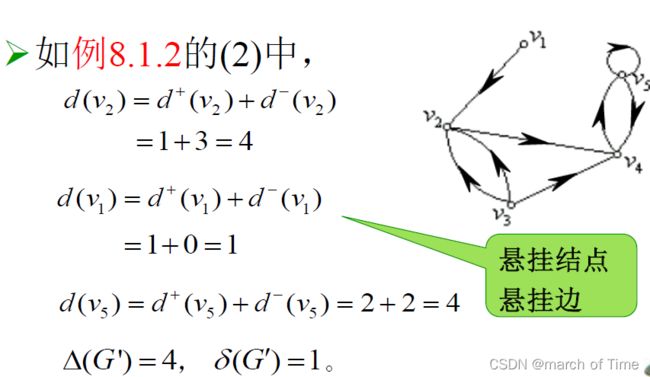
用邻接矩阵表示度数：

行元素之和为vi的出度
列元素之和等于vi的入度

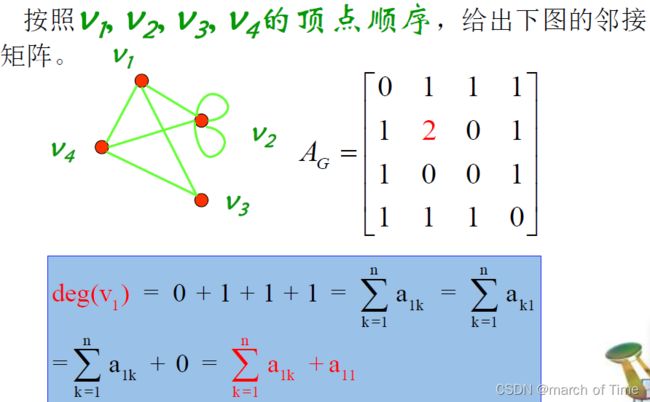
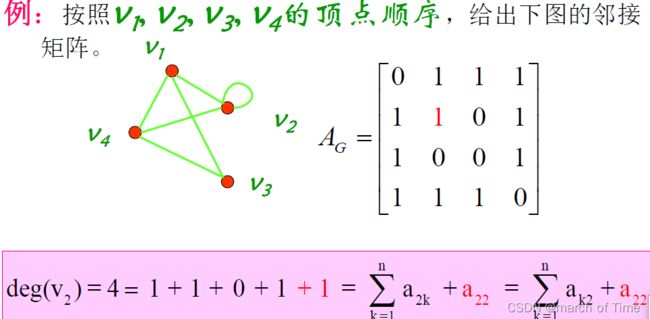
握手定理

可图化序列：

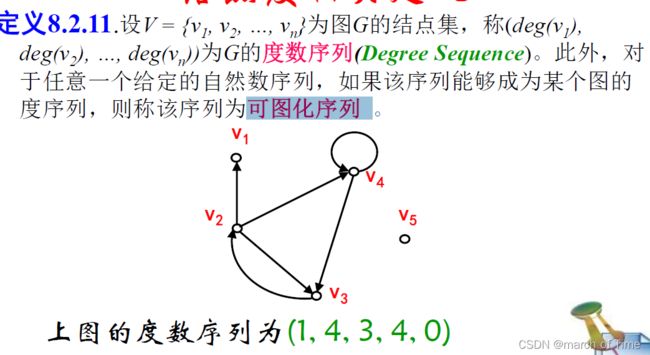
【例题】有一个警察追小偷进了一个有两个出入口的空宅。已知该宅中有奇数个相互连通的房间，每个房间有奇数个通往不同房间的门。若把住出入口，小偷能否逃出空宅？

【解】由题设及分析可知，空宅内通道图中，结点个数为奇数，每个结点的度数为奇数，根据图的度结构性质。 这是不可能的，所以宅内一定还有一处通往外面的密门，在出入口被堵的情况下，小偷有可能通过密门逃出空宅。

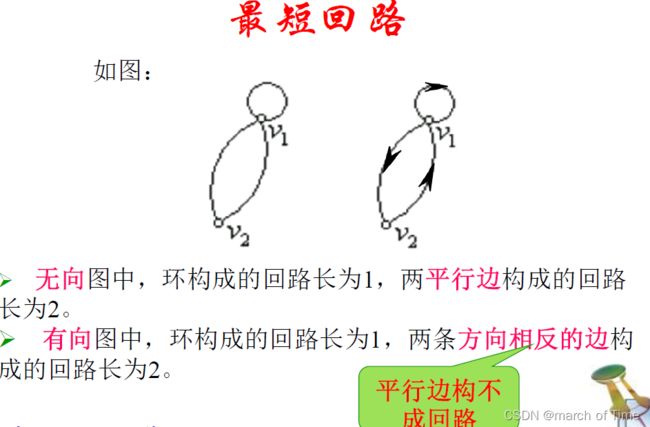
路与连通

基本通路一定是简单通路
简单边不同，基本点不同

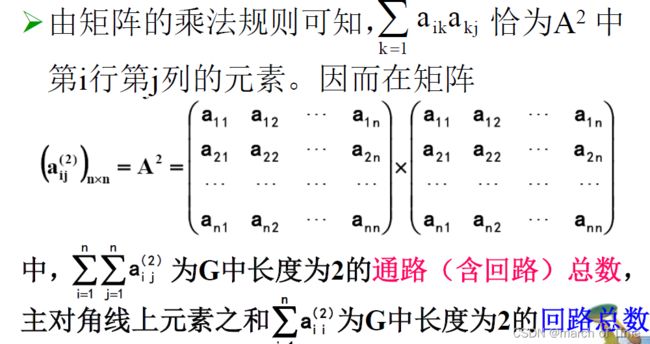
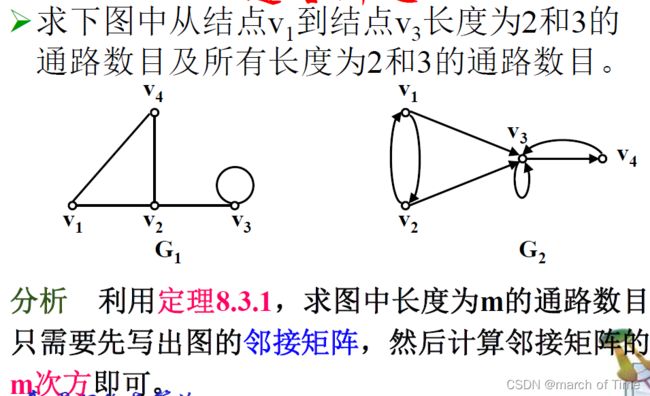
求两个结点之间长度为n的通路数目

从结点vi到vj长度为3的通路总数为：

通路定理

推论1
n 阶图中，若从顶点v i到 v j 存在
通路（两个节点不相等），则从 Vi 到v j 存在长度小于等于n -1的基本通路。
定理 在一个具有n个结点的图中，如果存在经过结点vi回路，则存在一条经过vi的长度不大于n的回路。
推论 在一个具有n个结点的图中，如果存在经过结点vi回路，则存在一条经过vi的长度不大于n的基本回路。

图的可达性

可达性矩阵

恒等关系IV等于矩阵的零次幂

若无向图每一对不同的顶点之间都有通路，则该图称为连通的，否则称为非连通图或分离图
无向完全图Kn（n≥1）都是连通图**，而多于一个结点的零图都是非连通图**。
非平凡无向线图G是连通图当且仅当它的可达性矩阵P的所有元素均为1。

连通分支



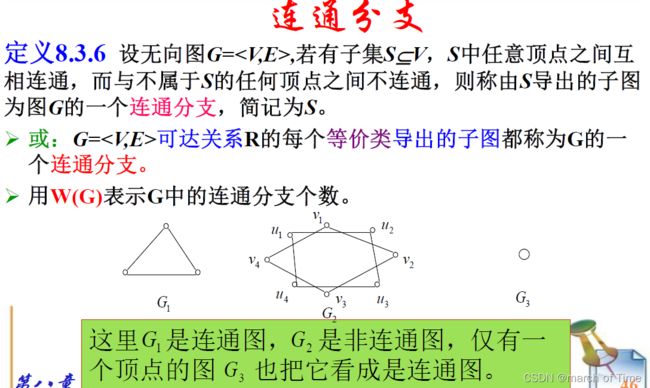
连通图可以看成是只有一个连通分
支的图， 即 W(G)=1。
或者：
若无向图G只有一个连通分支，则
称G是无向连通的。
【例题】： 假设=, 为任一给定的无向简单图，其中=，=，是其连通分支数，
证明：−（）≤。
证明：对作数学归纳法证明：
当=0时，是零图，（）=，命题成立。
设不等式对于−1成立，要证明对也成立。现从上删去一条边得′，则′有两种可能：
① ′有个结点，个连通分支，−1条边，根据归纳假设−≤−1，故有：
−≤−<；
② ′有个结点，+1个连通分支，−1条边，根据归纳假设：
−(+1)≤m−1
故有：
−≤m
成立。
故对一切，成立
−≤

割点割边

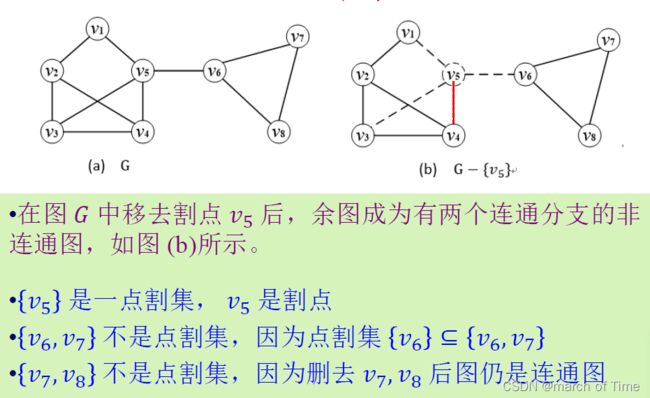
⨠⨠有时删除一个顶点和它所关联的边，就产生带有比原图更多连通分支的子图。把这样的顶点称为割点。从连通图里删除割点，就产生不连通的子图。
⨠⨠把一旦删除就产生带有比原图更多的连通分支的子图的边称为割边或桥。

定义8.3.8 无向图 =,，若存在的某个子集 ′⊆ ，使得 (−′)>() ，且对于 ′的任何真子集 ′′，有
（−′′)=()
则称 ′为 的点割集。如果点割集中只有一个结点 ，则称 为割点

无向图 =<,>，若存在边集 的某个子集′⊆ ，使得 (−′)>( )，且对于 ′的任何真子集 ′′，有
(−′′)=() 则称 ′为 的边割集。如果边割集中只有一条边 ，则称 为割边或桥。
总结：

⨠⨠(1)完全图 无点割集，因为从 中删除 ≤−1个顶点后，所得图仍然是连通的。
⨠⨠(2) 阶零图既无点割集也无边割集。
⨠⨠(3) 对于连通图 ，′为 的边割集，则必有 −′=2 。 因为删除一条边最多只能增加一个连通分支。
⨠⨠(4) 对于连通图 ，′为 的点割集，则 −′≥2，而且可能 −′>2，因为删除一个结点可能增加多个连通分支。
连通度：
（注意是最小的点割集的结点个数）

(1) 如果 是平凡图或非连通图，则规定
==；
(2) 如果 是完全图 ，由于 中无点割集，当删除 −1个顶点后， 为平凡图，故
=−。
(3) 如果 中存在割点，则 =；
如果 中存在割边，则 =。

有向图的连通性

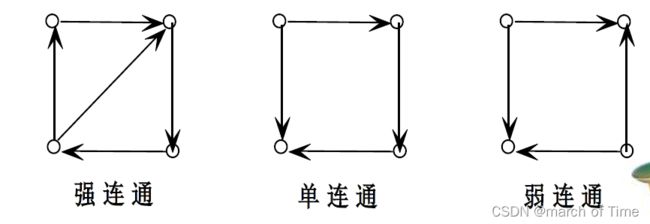
强连通图：若图中任何一对结点两者之间相互可达(两个方向)。
⨠⨠单连通图：任何一对结点间至少有一个结点到另一结点可达。 (单方向)
⨠⨠弱连通图：把有向图看成无向图时图是连通的。
对于弱分图，存在两个结点之间是不可达的

有向图G是强连通图的充分必要条件是G中存在一条经过所有结点的回路。
该定理给出了判断强连通图的简便方法。
有向图G是单向连通图的充分必要条件是G中存在一条经过所有结点的通路。
•该定理给出了判断单向连通图的简便方法。

一、如果不考虑边的方向，弱连通分支对应相应的无向图的连通分支。
二、注意把握（强、单向、弱）连通分支的极大性特点，即任意增加一个结点或一条边就不是（强、单向、弱）连通的了

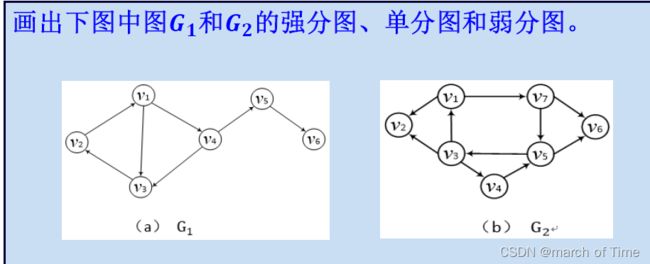
强分图 单分图 弱分图


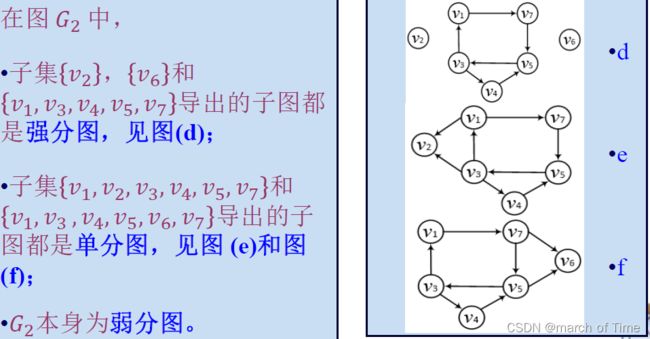
强连通的等价性
若在有向图G = 的结点集V上定义二元关系R为：∈R当且仅当vi和vj在同一强（弱）连通分支中，对一切vi,vj∈V。则R是一个等价关系。
这种等价关系把结点分成等价类，等价类的集合是V上的一个划分，每一个等价类的结点导出一个强（弱）连通分支。有如下三个定理
【定理】在有向图G = 中，它的每一个结点位于且仅位于一个强（弱）连通分支中。（对结点的分类）
【定理】在有向图G = 中，它的每一个结点至少位于一个单向连通分支中。 （对结点的聚类，相容关系）
【定理】在有向图G = 中，它的每一条边至多在一个强连通分支中，至少在一个单向连通分支中，在且仅在一个弱连通分支中。（对边的划分）