一文详细解释“核技巧”以及支持向量机
一文详细解释“核技巧”以及支持向量机
- 从支持向量机开始说起
-
- 什么是支持向量机
- 线性可分支持向量机
- 间隔最大化(支持向量机的本质)
- 引入对偶问题求解
- 拉格朗日对偶性
- 对偶问题
- 非线性支持向量机与核函数
-
- 核函数的定义
- 核技巧在支持向量机中的应用
- 常用的核函数
想写这篇博客是因为最近在研究迁移学习的过程中遇到了最大均值差异损失(MMD loss),这个损失我大致能明白是什么意思。
但是看看定义,最大均值差异是一种非参数度量,用于再生核希尔伯特空间中基于核嵌入来度量分布之间的距离。好家伙,再生核希尔伯特空间,核嵌入,懵懵懂懂。又因为在写代码时候经常调用高斯核函数,所以决定还是从头到尾弄清数学原理。
从支持向量机开始说起
我开始看的是李航的《统计学习方法》第7章支持向量机。
什么是支持向量机
我理解,就是在特征空间,注意,特征空间不是输入空间,找一条线把两个类别分开。SVM是一种二分类模型。我先不综述支持向量机有哪些内容,都摆出来大家就会头晕了。
线性可分支持向量机
考虑一个二类分类问题,假设输入空间与特征空间为两个不同的空间,输入空间为欧氏空间或离散集合,特征空间为欧式空间或希尔伯特空间。线性可分支持向量机、线性支持向量机假设两个空间的元素1、1对应,并将输入空间中的输入映射为特征空间中的特征向量。所以,支持向量机是在特征空间进行学习的。
看完这段话,我们首先建立一个概念,支持向量机就是在特征空间上找一条线(说分类器也行)。
什么是欧氏空间?
这是《矩阵分析》课本上一个关于欧式空间的定义(书有点乱)。我总结一下,就是对于一个实数域上的线性空间,如果其中任意两个向量都满足(1)(2)(3)(4)条,我们就把这个线性空间称为实内积空间,简称内积空间。然后在这个概念之下呢,把有限维实内积空间称为欧式空间。因为n维线性空间的内积定义如上所示,两个向量内积是元素相乘再相加,满足上述4条。总之,这就是一个欧式空间的概念。对于深度学习来说,输入一般都满足是在欧式空间。
那么什么是希尔伯特空间?
希尔伯特空间是欧式空间的一种拓展,拓展了什么呢?首先内积空间不仅定义了内积,也定义了其中向量的长度该怎么求。 ( α , α ) \sqrt{(\alpha,\alpha) } (α,α)称为向量 α \alpha α的长度,有了长度,有了内积,也有了角度的概念,对于任何两个维度相同的内积向量,角度的定义和高中学的夹角公式一样, ( α , β ) ∣ α ∣ ∣ β ∣ \frac{\sqrt{(\alpha ,\beta )}}{\left | \alpha \right |\left | \beta \right |} ∣α∣∣β∣(α,β)。希尔伯特空间在欧式空间的基础上将有限维的概念去掉,去掉有限维之后内积计算是出现无穷大怎么办?再定义其上所有的柯西序列都收敛。一个内积空间,当作为一个赋范向量空间是完备的时候,就是希尔伯特空间。所以,通俗点,希尔伯特空间是一个无限维的内积计算结果收敛的内积空间
了解了欧式空间和希尔伯特空间的定义,我们回头再来继续看支持向量机。我先把书上的内容放到下面


求解凸二次规划问题学习得到分离超平面就不详细解释了,我们需要知道的是,这个超平面简单的可以用公式
ω ∗ ⋅ x + b ∗ = 0 \omega ^{*}\cdot x+b^{*}=0 ω∗⋅x+b∗=0来表示。第二,在 ω ⋅ x + b = 0 \omega \cdot x+b=0 ω⋅x+b=0确定的情况下, ∣ ω ⋅ x + b ∣ |\omega \cdot x+b| ∣ω⋅x+b∣可以相对的表示点x距离超平面的远近,因为这个原因,给它再乘上一个y,就可以相对的表示分类的正确性和确信度,这个称为函数间隔。如果把函数间隔的公式除一个法向量的长度,也就是 L 2 L_{2} L2范数,其实就是一个单位化操作。函数间隔就变成了几何间隔。以后基本不用函数间隔了,用几何间隔,因为几何间隔不会随着超平面参数成比例的改变而改变。
间隔最大化(支持向量机的本质)
支持向量机学习的基本想法就是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。对于线性可分的情况,可能分离超平面有很多,有很多线可以把它们分开,但是只有一条线,可以分出最大的几何间隔。也就是说,间隔最大化,不仅要将正负实例点分开,而且对最难分的实例点也有足够的确信度将它们分开。
到了如何求这个最大分离超平面的时候了。实际上我们可以将它转化成一个约束最优化问题。

对于平面上所有的点,我们希望找到一条“直线”使得所有点距离这条直线的几何间隔最大。这个问题可以改写为:
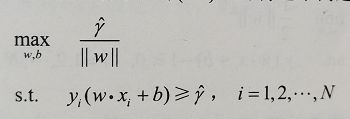
求函数间隔最大,然而函数间隔是可以随着w和b成比例变化的,也就是这个解,可想而知,w和x是成对成比例的,然而我们只需要一个解就好了,所以这个时候固定函数间隔为1,然后再求,这样就可以得到一个固定的解。然后当 ∣ ∣ γ ^ ∣ ∣ = 1 ||\hat{\gamma }||=1 ∣∣γ^∣∣=1时,问题也就变成了求 1 ∣ ∣ ω ∣ ∣ \frac{1}{||\omega ||} ∣∣ω∣∣1的最大值,这在数学上和求 1 2 ∥ ω ∥ 2 \frac{1}{2}\left \| \omega \right \|^{2} 21∥ω∥2的最小值是等价的,所以就可以转换为一个凸优化问题的求解。
解的唯一性和存在性就不证明了,知道结论其实就可以了,然后需要知道使得约束条件等于0的点 y i ( ω ⋅ x i + b ) − 1 = 0 y_{i}(\omega \cdot x_{i}+b)-1=0 yi(ω⋅xi+b)−1=0就是支持向量。(这个支持向量和1的关系是这样来的,我之前一直不理解为什么是1)
引入对偶问题求解
为什么要引入对偶问题求解?一是因为对偶问题更容易求解,二是因为自然引入核函数,进而推广到分线性分类问题。
在这里我们终于见到了核函数的出现。
重申一下,现在我们的约束最优化问题变成了求解:
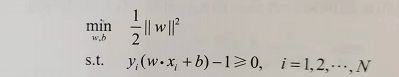
在这里又要补充两个概念,拉格朗日函数以及对偶性问题求解,请大家再坚持一下!!!
在约束最优化问题中,常常利用拉格朗日对偶性将原始问题转换为对偶问题,通过解对偶问题得到原始问题的解。
拉格朗日对偶性
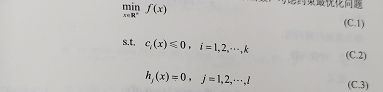
我们将上述公式称为原始最优化问题,这样的定义出现在很多讲最优化的课本中,原始最优化问题也简称为原始问题。
接下来引入拉格朗日函数:
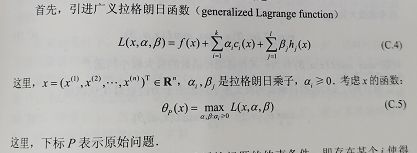
先摆出结论,对于一个求 f ( x ) f(x) f(x)的极小值问题,可以转换为求拉格朗日函数形式的 L ( x , α , β ) L(x,\alpha,\beta) L(x,α,β)的极大值问题(这里的 α , β \alpha,\beta α,β都是大于等于0的)。
为什么呢?因为 c i ( x ) 和 h i ( x ) c_{i}(x)和h_{i}(x) ci(x)和hi(x)是原始问题的约束条件,如果 c i ( x ) 和 h j ( x ) c_{i}(x)和h_{j}(x) ci(x)和hj(x)不满足原始条件,大于零或者不等于零,因为 α \alpha α和 β \beta β都大于零,该问题极大值就可以取 α \alpha α或 β \beta β为无穷大而取无穷大的极值。如果x满足约束条件,那么 L ( x , α , β ) L(x,\alpha,\beta) L(x,α,β)的极大值就和 f ( x ) f(x) f(x)相等了。因为满足条件,所有的 h j ( x ) h_{j}(x) hj(x)为零,所有的 c i ( x ) c_{i}(x) ci(x)小于零。这样分析完,我们就得出一个结论。

可以等价后,把原始问题的极小值问题转化为用拉格朗日函数表述的形式,也就是一个先求一个变量为 α \alpha α或 β \beta β的拉格朗日函数的极大值使之可以与原问题等价,再求一个变量为x的原问题的极小值问题。这样说有点绕,需要多捋几次这中间的关系,不然不理解为什么原问题求解可以转化为拉格朗日函数的极小极大值问题。

不理解也可以,只需要知道我们经过进一步变换又把一个问题改头换面了,现在求解的目标就是这个函数了。
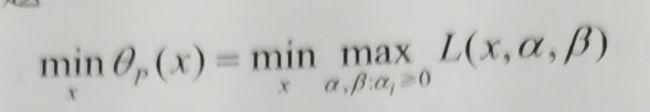
对偶问题
给一个简单的定义,上述函数是先求极大值再求极小值,对偶问题是先求极小值再求极大值,但两者的最优值不是任何情况下相等的,存在着如下关系。


这一块儿感兴趣的可以再探究,我只说这一步的目的还是为了更好的求解一个最优化问题而引入这么一个对偶问题求解的方法,图上推论C.1的结论可以记一下,如果这三个未知量的解分别是原始问题和对偶问题的可行解,而且最优值此时求得是相同的,那么此时的可行解就进化成了最优解。也就是说可以用对偶问题的解来当作原问题的解。
在引入了这两种方法之后,我们的原始问题的解,就可以表示为(此处忽略求解过程)
ω ∗ = ∑ α i ∗ y i x i \omega ^{*}=\sum \alpha _{i}^{*}y_{i}x_{i} ω∗=∑αi∗yixi,其中 α ∗ \alpha ^{*} α∗是已经求解得到的对偶最优化问题的解。
b ∗ = y j − ∑ i = 1 N α i ∗ ( x ⋅ x i ) b^{*}=y_{j}-\sum_{i=1}^{N}\alpha _{i}^{*}(x\cdot x_{i}) b∗=yj−∑i=1Nαi∗(x⋅xi)
分离超平面可以写成
∑ i = 1 N α i ∗ ( x ⋅ x i ) + b ∗ = 0 \sum_{i=1}^{N}\alpha _{i}^{*}(x\cdot x_{i})+b^{*}=0 ∑i=1Nαi∗(x⋅xi)+b∗=0
分类决策函数可以写成:
f ( x ) = s i g n ( ∑ i = 1 N α i ∗ ( x ⋅ x i ) + b ∗ ) f(x)=sign(\sum_{i=1}^{N}\alpha _{i}^{*}(x\cdot x_{i})+b^{*}) f(x)=sign(∑i=1Nαi∗(x⋅xi)+b∗)
最重要的一句话,看这个表示形式,也就是说,分类决策函数只依赖于输入x和训练样本输入的内积。
非线性支持向量机与核函数
终于到了要解读核函数的时候了,对于解线性分类问题,线性分类支持向量机是一种非常有效的方法。但是,有时分类问题是非线性的,这时可以使用非线性支持向量机。其主要特点就是利用核技巧。
举个例子:

左图在原平面上只有取一个超曲面才能将两类分开,但如果引入一个非线性变换后,在右图上的平面就可以很好地将两类分开。所以,我们最直接的想法就是,可不可以依然用线性分类问题求解,只是需要将输入经过一个非线性变换转换到另一个空间内,在这个空间内用线性分类问题解决。
核技巧应用到支持向量机,其基本想法就是通过一个非线性变换将输入空间(欧氏空间 R n R^{n} Rn或离散集合)对应于一个特征空间(希尔伯特空间),使得在输入空间中的超曲面模型对应于特征空间中的超平面模型,这样,分类问题的学习任务通过在特征空间中求解线性支持向量机就可以完成。
核函数的定义
李航《统计学习方法》解释的非常清楚,在这里我基本引用书上原文做个解释。
核函数的定义:
设 χ \chi χ是输入空间(欧式空间或离散集合),又设 H H H为特征空间(希尔伯特空间),如果存在一个映射,从 χ \chi χ到 H H H
ϕ ( x ) : χ → H \phi (x):\chi \rightarrow H ϕ(x):χ→H
使得对于所有的 ( x , z ) ∈ χ (x,z)\in \chi (x,z)∈χ,函数 K ( x , z ) K(x,z) K(x,z)满足条件:
K ( x , z ) = ϕ ( x ) ⋅ ϕ ( z ) K(x,z) = \phi(x)\cdot\phi(z) K(x,z)=ϕ(x)⋅ϕ(z)
则称 K ( x , z ) K(x,z) K(x,z)为核函数, ϕ ( x ) \phi(x) ϕ(x)为映射函数,式中 ϕ ( x ) ⋅ ϕ ( z ) \phi(x)\cdot\phi(z) ϕ(x)⋅ϕ(z)为 ϕ ( x ) \phi(x) ϕ(x)和 ϕ ( z ) \phi(z) ϕ(z)的内积

结论,定义核函数比定义映射算内积容易很多,缺点就是,一个核函数你可能找出很多映射以及很多特征空间符合这个核函数,所以这个时候也可以理解为什么特征空间是希尔伯特空间了,当然我们一般真的实际应用是不可能出现无限维的特征空间了,是理论上这个核函数可以找到一个无限维的特征空间。
核技巧在支持向量机中的应用
终于是不白费我们花大量力气算一个内积形式表示的分类超平面了!!!
我们注意到,在线性支持向量机的对偶问题中,无论是目标函数还是决策函数(分离超平面)都只涉及输入实例与实例之间的内积。在对偶问题的目标函数中的内积 x i ⋅ x j x_{i} \cdot x_{j} xi⋅xj可以用核函数 K ( x i ⋅ x j ) = ϕ ( x i ) ⋅ ϕ ( x j ) K(x_{i} \cdot x_{j}) = \phi(x_{i}) \cdot \phi(x_{j}) K(xi⋅xj)=ϕ(xi)⋅ϕ(xj)来代替

这等价于经过映射函数 ϕ \phi ϕ将原来的输入空间变换到一个新的特征空间,将输入空间中的内积变换为特征空间中的内积 ϕ ( x i ) ⋅ ϕ ( x j ) \phi(x_{i}) \cdot \phi(x_{j}) ϕ(xi)⋅ϕ(xj),在新的特征空间里从训练样本中学习线性支持向量机,当映射函数是非线性函数时,学习到的含有核函数的支持向量机时非线性分类模型。
也就是说,在核函数给定的条件下,可以利用线性分类问题的方法求解非线性分类问题的支持向量机,学习是隐式地在特征空间进行地,不需要显式地定义特征空间核映射函数,这样地技巧称为核技巧。(核技巧之所以称为技巧看来是有一定说法的,从这里就可以看出)。
关于正定核的内容就不介绍了,正定核说的是什么样的函数才能成为核函数的事情。

