博弈（alpha-beta 剪枝）POJ —— 1085 Triangle War

对应 poj 题目：点击打开链接

Triangle War

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 3066		Accepted: 1207

Description

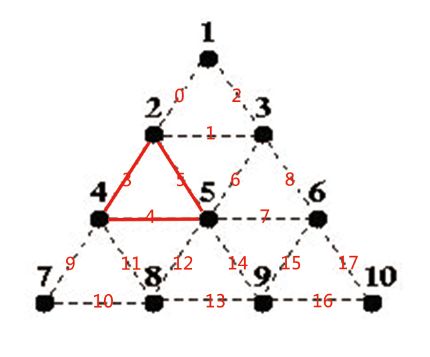
Triangle War is a two-player game played on the following triangular grid: 

Two players, A and B, take turns filling in any dotted line connecting two dots, with A starting first. Once a line is filled, it cannot be filled again. If the line filled by a player completes one or more triangles, she owns the completed triangles and she is awarded another turn (i.e. the opponent skips a turn). The game ends after all dotted lines are filled in, and the player with the most triangles wins the game. The difference in the number of triangles owned by the two players is not important. 

For example, if A fills in the line between 2 and 5 in the partial game on the left below: 

Then, she owns the triangle labelled A and takes another turn to fill in the line between 3 and 5. B can now own 3 triangles (if he wishes) by filling in the line between 2 and 3, then the one between 5 and 6, and finally the one between 6 and 9. B would then make one more move before it is A's turn again. 
In this problem, you are given a number of moves that have already been made. From the partial game, you should determine which player will win assuming that each player plays a perfect game from that point on. That is, assume that each player always chooses the play that leads to the best possible outcome for himself/herself.

Input

You will be given a number of games in the input. The first line of input is a positive integer indicating the number of games to follow. Each game starts with an integer 6 <= m <= 18 indicating the number of moves that have been made in the game. The next m lines indicate the moves made by the two players in order, each of the form i j (with i < j) indicating that the line between i and j is filled in that move. You may assume that all given moves are legal.

Output

For each game, print the game number and the result on one line as shown below. If A wins, print the sentence "A wins." If B wins, print "B wins."

Sample Input

4 
6 
2 4 
4 5 
5 9 
3 6 
2 5 
3 5 
7 
2 4 
4 5 
5 9 
3 6 
2 5 
3 5 
7 8 
6 
1 2 
2 3 
1 3 
2 4 
2 5 
4 5 
10 
1 2 
2 5 
3 6 
5 8 
4 7 
6 10 
2 4 
4 5 
4 8 
7 8 

Sample Output

Game 1: B wins. 
Game 2: A wins. 
Game 3: A wins. 
Game 4: B wins.

题意：

        游戏有A、B两人参与。A先走，每人每次任选一条虚线填成实线。而如果某人填完一条线段后，该线段与另外两条相邻的实线组成了一个单位三角形，该三角形被标记为该游戏者所有，且该游戏者必须接着再填一条虚线。当18条线段被填充完毕后，拥有三角形多的玩家获胜。

        首先输入一个数 T ，表示试验次数；接着一个数 n，表示当前局面已经走了 n 条边；接着输入 n 对数，每对数字表示一条填充边，由 A 开始。问从给出的局面开始，双方都采取最优策略，最终谁会取胜。

思路：

        显然是博弈问题，也是 alpha-beta 搜索算法的基础应用（博弈基础：点击打开链接）。一个比较关键的问题是局面的存储。整个棋盘有18条边，因此可以用一个整型来存储一个局面，具体就是：

        如果每条边用红色数字表示（当然也可以不这样排列），则用 2^0 = 1 表示 edge(1, 2) 或 edge(2, 1)，用 2^1 = 2(即二进制10)表示 edge(2, 3) 或 edge(3, 2)，用2^2 = 4(即二进制100)表示 edge(1, 3) 或 edge(3, 1) ... 

        那这个局面用哪个数存储？用 2^3 + 2^4 + 2^5 = 56 表示；其余单位三角形可用同样的方法计算。

#include 
#include 
#include 

// 保存每条边代表的数字
int edge[11][11]={  
	{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},    
	{0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0},    
	{0, 0, 0, 1, 3, 5, 0, 0, 0, 0, 0},    
	{0, 2, 1, 0, 0, 6, 8, 0, 0, 0, 0},    
	{0, 0, 3, 0, 0, 4, 0, 9, 11,0, 0},    
	{0, 0, 5, 6, 4, 0, 7, 0, 12,14,0},    
	{0, 0, 0, 8, 0, 7, 0, 0, 0, 15,17},    
	{0, 0, 0, 0, 9, 0, 0, 0, 10,0, 0},    
	{0, 0, 0, 0, 11,12,0, 10,0, 13, 0},    
	{0, 0, 0, 0, 0, 14,15,0, 13, 0, 16},    
	{0, 0, 0, 0, 0, 0, 17,0, 0, 16,0},    
};    
// 保存每个单位三角形代表的数字
int tri[9] = {7, 56, 98, 448, 3584, 6160, 28672, 49280, 229376};    
int end_state = (1<<18)-1; // 终结状态 2^18 - 1 ，即所有边均被填充
int inf = (1<<20);

int next_state(int cur_state, int edge, int *cnt)
{
	int i;
	int new_state = (cur_state | edge); // 当前局面并上一条边形成新局面
	for(i = 0; i < 9; i++) // 如果新局面能形成一个新的单位三角形，则 cnt++
		if(((cur_state & tri[i]) != tri[i]) && ((new_state & tri[i]) == tri[i]))
			(*cnt)++;
	return new_state;
}

int alpha_beta(int player, int cur_state, int alpha, int beta, int ca, int cb)
{
	int remain;
	// 如 A 得到 5 分以上则 A 赢
	// 如 B 得到 5 分以上则 A 输
	if(ca >= 5) return 1;
	if(cb >= 5) return -1;
	remain = ((~cur_state) & end_state); // 计算剩余可走的边
	if(player){ // A 走
		while(remain){ // 有可走边
			int move = (remain & (-remain)); // 选择一条可走边
			int ta = ca;
			int val;
			// A 填了边后形成新的局面
			int new_state = next_state(cur_state, move, &ta);
			if(ta > ca) // 如果 A 得分了，则 A 继续填一条边
				val = alpha_beta(player, new_state, alpha, beta, ta, cb);
			else // 否则轮到 B 填
				val = alpha_beta(player^1, new_state, alpha, beta, ca, cb);
			if(val > alpha)
				alpha = val;
			if(alpha >= beta) 
				return alpha;
			remain -= move; // 把边 move 从剩余可选边 remain 中移除
		}
		return alpha;
	}
	else{ // B 走
		while(remain){
			int move = (remain & (-remain));
			int tb = cb;
			int val;
			int new_state = next_state(cur_state, move, &tb);
			if(tb > cb)
				val = alpha_beta(player, new_state, alpha, beta, ca, tb);
			else
				val = alpha_beta(player^1, new_state, alpha, beta, ca, cb);
			if(val < beta)
				beta = val;
			if(alpha >= beta)
				return beta;
			remain -= move;
		}
		return beta;
	}
}

int main()
{
#if 0
	freopen("in.txt","r",stdin);
#endif
	int T, w = 0;
	scanf("%d", &T);
	while(T--){
		int i;
		int n;
		int ans;
		int cnt = 0; // 偶数轮到 A 走，奇数轮到 B 走
		int cur_state = 0; // 当前局面
		int ca = 0; // A 的得分
		int cb = 0; // B 的得分
		int ta, tb;
		int alpha = -inf;
		int beta = inf;
		scanf("%d", &n);
		for(i = 0; i < n; i++){
			int u, v;
			ta = ca;
			tb = cb;
			scanf("%d%d", &u, &v);
			cur_state = next_state(cur_state, 1< 0)
			printf("Game %d: A wins.\n", ++w);
		else
			printf("Game %d: B wins.\n", ++w);
	}
	return 0;
}