强连通分量
有向图中, u可达v不一定意味着v可达u. 相互可达则属于同一个强连通分量(Strongly Connected Component, SCC)
1、强连通图。在一个强连通图中,任意两个点都通过一定路径互相连通。比如图一是一个强连通图,而图二不是。因为没有一条路使得点4到达点1、2或3。

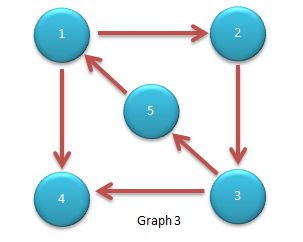
2、强连通分量。在一个非强连通图中极大的强连通子图就是该图的强连通分量。比如图三中子图{1,2,3,5}是一个强连通分量,子图{4}是一个强连通分量。
Kosaraju算法
算法步骤
调用DFS(G), 计算出每个结点的f[u]
计算GT
调用DFS(GT), 在主循环中按照f[u]递减的顺序执行DFS-VISIT, 则得到的每个DFS树恰好对应于一个SCC
运行时间:O(n+m)
算法示例: 先把f[u]排序成postI数组, 然而在GT上DFS
SCC的f性质
当按照f值排序以后, 第二次DFS是按照SCC的拓扑顺序进行(以后所指d[u]和f[u]都是第一次DFS所得到的值)
记d(C)和f(C)分别表示集合C所有元素的最早发现时间和最晚完成时间, 有如下定理:
定理: 对于两个SCC C和C’, 如果C到C’有边, 则f(C)>f(C’)
情况一: d(C) < d(C’), 考虑C中第一个被发现的点x, 则C’全为白色, 而C到C’有边, 故x到C’中每个点都有白色路径. 这样, C和C’全是x的后代, 因此f(C) > f(C’)
情况二: d(C) > d(C’). 由于从C’不可到达C, 因此必须等C’全部访问完毕才能访问C. 因此f(C) > f(C’)
推论:对于两个SCC C和C’, 如果在GT中C到C’有边, 则f(C)
Kosaraju算法的正确性
首先考虑f(C)最大的强连通分量. 显然, 此次DFS将访问C的所有点, 问题是是否可能访问其他连通分量的点? 答案是否定的, 因为根据推论, 如果在GT中C到另外某个C’存在边, 一定有f(C)
Tarjan算法
其实,tarjan算法的基础是DFS。我们准备两个数组Low和Dfn。Low数组是一个标记数组,记录该点所在的强连通子图所在搜索子树的根节点的Dfn值(很绕嘴,往下看你就会明白),Dfn数组记录搜索到该点的时间,也就是第几个搜索这个点的。根据以下几条规则,经过搜索遍历该图(无需回溯)和对栈的操作,我们就可以得到该有向图的强连通分量。
1、数组的初始化:当首次搜索到点p时,Dfn与Low数组的值都为到该点的时间。
2、堆栈:每搜索到一个点,将它压入栈顶。
3、当点p有与点p’相连时,如果此时(时间为dfn[p]时)p’不在栈中,p的low值为两点的low值中较小的一个。
4、当点p有与点p’相连时,如果此时(时间为dfn[p]时)p’在栈中,p的low值为p的low值和p’的dfn值中较小的一个。
5、每当搜索到一个点经过以上操作后(也就是子树已经全部遍历)的low值等于dfn值,则将它以及在它之上的元素弹出栈。这些出栈的元素组成一个强连通分量。
6、继续搜索(或许会更换搜索的起点,因为整个有向图可能分为两个不连通的部分),直到所有点被遍历。
由于每个顶点只访问过一次,每条边也只访问过一次,我们就可以在O(n+m)的时间内求出有向图的强连通分量。但是,这么做的原因是什么呢?
Tarjan算法的操作原理如下:
1、Tarjan算法基于定理:在任何深度优先搜索中,同一强连通分量内的所有顶点均在同一棵深度优先搜索树中。也就是说,强连通分量一定是有向图的某个深搜树子树。
2、可以证明,当一个点既是强连通子图Ⅰ中的点,又是强连通子图Ⅱ中的点,则它是强连通子图Ⅰ∪Ⅱ中的点。
3、这样,我们用low值记录该点所在强连通子图对应的搜索子树的根节点的Dfn值。注意,该子树中的元素在栈中一定是相邻的,且根节点在栈中一定位于所有子树元素的最下方。
4、强连通分量是由若干个环组成的。所以,当有环形成时(也就是搜索的下一个点已在栈中),我们将这一条路径的low值统一,即这条路径上的点属于同一个强连通分量。
5、如果遍历完整个搜索树后某个点的dfn值等于low值,则它是该搜索子树的根。这时,它以上(包括它自己)一直到栈顶的所有元素组成一个强连通分量。
Tarjan模版:
 View Code
View Code
2 #include <iostream>
3 #include <cstring>
4 #include <cstdio>
5 #include <stack>
6 #define max(a,b) (a>b?a:b)
7 #define min(a,b) (a>b?b:a)
8 using namespace std;
9
10 const int N= 1001;
11 int time= 1;
12 int low[N],dfn[N];
13 bool instack[N];
14 stack< int>st;
15
16 struct LIST
17 {
18 int v;
19 LIST *next;
20 };
21 LIST *head[N]={NULL};
22
23 void tarjan( int v) /* tarjan求强连通分支 */
24 {
25 dfn[v]=low[v]=time++; /* 标记点v的DFS遍历序号 */
26 st.push(v); /* 将点v入栈 */
27 instack[v]= true; /* 标记点v已经在栈中 */
28 for(LIST *p=head[v];p!=NULL;p=p->next) /* 遍历V能直接到达的点 */
29 {
30 if(!dfn[p->v]) /* 如果v的邻接点没有入过栈 */
31 {
32 tarjan(p->v);
33 low[v]=min(low[v],low[p->v]); /* 如果v能直接到达的这个点没在栈中,v的最早祖先为他们中的较小值 */
34 }
35 else if(instack[p->v]) /* 如果在栈中 */
36 low[v]=min(low[v],dfn[p->v]); /* 如果在栈中,则v的最早祖先是他的序号和那个点的序号较小的 */
37 }
38 if(dfn[v]==low[v]) /* 如果dfn[v]和low[v]相等,则说明v点是其所属强连通分支DFS遍历起点,这个强连通分支所有点都在v点之上 */
39 {
40 cout<< " { ";
41 do
42 {
43 v=st.top();
44 st.pop();
45 instack[v]= false;
46 cout<<v<< ' ';
47 } while(dfn[v]!=low[v]);
48 cout<< " } "<<endl;
49 }
50 }
51
52 int main()
53 {
54 int i,j,n,m;
55 cin>>n;
56 while(!st.empty())
57 st.pop();
58 memset(dfn, 0, sizeof(dfn));
59 memset(instack, false, sizeof(instack));
60 for(i= 0;i<=n;i++)
61 head[i]=NULL;
62 for(i= 1;i<=n;i++)
63 {
64 cin>>m; // i的邻接点数量
65 // 输入每个邻接点编号
66 LIST *rear=head[i];
67 for(j= 0;j<m;j++) /* 创建邻接表 */
68 {
69 if(!j)
70 {
71 rear= new LIST;
72 head[i]=rear;
73 }
74 else
75 {
76 rear->next= new LIST;
77 rear=rear->next;
78 }
79 rear->next=NULL;
80 cin>>rear->v;
81 }
82 }
83 for(i= 1;i<=n;i++)
84 if(!dfn[i]) /* 如果i没有入过栈 */
85 tarjan(i);
86 return 0;
87 }
88
POJ 1523 SPF
一道题看书+读题+写代码 写了一个上午,太弱了。
代码:
 View Code
View Code
2 #include <iostream>
3 #include <cstring>
4 #include <cstdio>
5 using namespace std;
6 const int N= 1001;
7 int map[N][N]; // 邻接矩阵
8 int vis[N]; // 标记是否访问过
9 int dfn[N]; // 每个顶点的dfn值
10 int low[N]; // 每个顶点的low值,用于判断是否是关节点
11 int num[N]; // 每个节点的连通分量个数
12 int n; // 节点个数
13 int son; // 根节点孩子个数,大于2则根节点为关节点
14 int times; // 搜索次序
15 void dfs( int u)
16 {
17 vis[u]= 1;
18 int i;
19 for(i= 1;i<=n;i++)
20 {
21 // i与u邻接则:①i是u的祖先(i,u)是回边
22 // ②i是u的儿子节点
23 if(map[u][i])
24 {
25 if(!vis[i]) // ②
26 {
27 times++;
28 low[i]=dfn[i]=times;
29 dfs(i);
30 low[u]=min(low[u],low[i]);
31 if(low[i]>=dfn[u])
32 {
33 if(u!= 1)
34 num[u]++;
35 else
36 son++; // 根节点
37 }
38 }
39 else
40 {
41 low[u]=min(low[u],dfn[i]);
42 }
43 }
44 }
45 }
46 void init()
47 {
48 son= 0;
49 times= 1;
50 low[ 1]=dfn[ 1]= 1;
51 memset(vis, 0, sizeof(vis));
52 memset(num, 0, sizeof(num));
53 }
54 int main()
55 {
56 init();
57 int i,u,v,flag,k= 0,m;
58 while(~scanf( " %d ",&u))
59 {
60 if(!u)
61 break;
62 memset(map, 0, sizeof(map));
63 scanf( " %d ",&v);
64 map[u][v]=map[v][u]= 1;
65 m=max(u,v);
66 n=max(m,n);
67 while(~scanf( " %d ",&u))
68 {
69 if(!u)
70 break;
71 scanf( " %d ",&v);
72 map[u][v]=map[v][u]= 1;
73 m=max(u,v);
74 n=max(m,n);
75 }
76 if(k> 0)
77 puts( "");
78 k++;
79 printf( " Network #%d\n ",k);
80 init();
81 dfs( 1);
82 if(son> 1)
83 num[ 1]=son- 1;
84 flag= 0;
85 for(i= 1;i<=n;i++)
86 {
87 if(num[i])
88 {
89 flag= 1;
90 printf( " SPF node %d leaves %d subnets\n ",i,num[i]+ 1);
91 }
92 }
93 if(!flag)
94 {
95 puts( " No SPF nodes ");
96 }
97 }
98 return 0;
99
100 }
101
POJ 1144 Network
模版题,求关节点数量
代码:
 View Code
View Code
2 #include <iostream>
3 #include <cstring>
4 #include <cstdio>
5 using namespace std;
6 const int N= 1001;
7 int map[N][N],vis[N],dfn[N],low[N],num[N];
8 int n,son,times;
9 void dfs( int u)
10 {
11 vis[u]= 1;
12 int i;
13 for(i= 1;i<=n;i++)
14 {
15 if(map[u][i])
16 {
17 if(!vis[i])
18 {
19 times++;
20 low[i]=dfn[i]=times;
21 dfs(i);
22 low[u]=min(low[u],low[i]);
23 if(low[i]>=dfn[u])
24 {
25 if(u!= 1)
26 num[u]++;
27 else
28 son++;
29 }
30 }
31 else
32 {
33 low[u]=min(low[u],dfn[i]);
34 }
35 }
36 }
37 }
38 void init()
39 {
40 son= 0;
41 times= 1;
42 low[ 1]=dfn[ 1]= 1;
43 memset(vis, 0, sizeof(vis));
44 memset(num, 0, sizeof(num));
45 memset(map, 0, sizeof(map));
46 }
47 int main()
48 {
49 init();
50 int i,u,v,s,m;
51 while(scanf( " %d ",&n)!=EOF && n)
52 {
53 s= 0;
54 init();
55 while(scanf( " %d ",&u) && u)
56 {
57 while(getchar()!= ' \n ')
58 {
59 scanf( " %d ",&v);
60 map[u][v]= 1;
61 map[v][u]= 1;
62 }
63 }
64 dfs( 1);
65 if(son> 1)
66 num[ 1]=son- 1;
67 for(i= 1;i<=n;i++)
68 {
69 if(num[i])
70 {
71 s++;
72 }
73 }
74 printf( " %d\n ",s);
75 }
76 return 0;
77 }
78
