LINGO基础学习笔记（二）

LINGO 函数

本文主要关于LINGO 有的9 种类型的函数，具体如下：

1、基本运算符

1） 算术运算符

算术运算符是针对数值进行操作的。LINGO 提供了 5 种二元运算符，分别为：
＾ 乘方
﹡ 乘
／ 除
﹢ 加
﹣ 减
LINGO 唯一的一元算术运算符是取反函数“﹣”。
这些运算符的优先级由高到底为：
﹣（取反）
＾
﹡／
﹢﹣
运算符的运算次序为从左到右按优先级高低来执行。 运算的次序可以用圆括号“（）”来改变。

2）逻辑运算符

在 LINGO 中，逻辑运算符主要用于集循环函数的条件表达式中，在创建稀疏集时用在成员资格过滤器中。
LINGO 具有９种逻辑运算符：
#not# 否定该操作数的逻辑值，＃not＃是一个一元运算符
#eq# 若两个运算数相等，则为 true；否则为 flase
#ne# 若两个运算符不相等，则为 true；否则为 flase
#gt# 若左边的运算符严格大于右边的运算符，则为 true；否则为 flase
#ge# 若左边的运算符大于或等于右边的运算符，则为 true；否则为 flase
#lt# 若左边的运算符严格小于右边的运算符，则为 true；否则为 flase
#le# 若左边的运算符小于或等于右边的运算符，则为 true；否则为 flase
#and# 仅当两个参数都为 true 时，结果为 true；否则为 flase
#or# 仅当两个参数都为 false 时，结果为 false；否则为 true
这些运算符的优先级由高到低为：
#not#（高）
#eq# #ne# #gt# #ge# #lt# #le#
#and# #or#（低）

3）关系运算符

在 LINGO 中， 关系运算符主要是被用在模型中， 来指定一个表达式的左边是否等于、小于等于、或者大于等于右边，形成模型的一个约束条件。
LINGO 有三种关系运算符：“=”、“<=”和“>=”。LINGO 中还能用“<”表示小于等于关系，“>”表示大于等于关系。
注意：LINGO 并不支持严格小于和严格大于关系运算符。
然而，如果需要严格小于和严格大于关系，比如让 A 严格小于 B：
A 那么可以把它变成如下的小于等于表达式：
A+ε<=B，
这里ε是一个小的正数，它的值依赖于模型中 A 小于 B 多少才算不等。

总：以上三类操作符的优先级：
高 #not# ﹣（取反）
＾
﹡ ／
﹢﹣
#eq# #ne# #gt# #ge# #lt# #le#
#and# #or#
低 <= = >=

2、数学函数

LINGO 提供了大量的标准数学函数：
@abs(x)：返回 x 的绝对值。
@sin(x)：返回 x 的正弦值，x 采用弧度制。
@cos(x)：返回 x 的余弦值。
@tan(x)：返回 x 的正切值。
@exp(x)：返回常数 e 的 x 次方。
@log(x)：返回 x 的自然对数。
@lgm(x)：返回 x 的 gamma 函数的自然对数。
@mod(x,y)：返回 x 除以 y 的余数。
@sign(x)：如果 x<0 返回-1；否则，返回 1。
@floor(x)：返回 x 的整数部分。当 x>=0 时，返回不超过 x 的最大整数；当 x<0
时，返回不低于 x 的最大整数。
@smax(x1,x2,…,xn)：返回 x1，x2，…，xn 中的最大值。
@smin(x1,x2,…,xn)：返回 x1，x2，…，xn 中的最小值。

3、金融函数

目前 LINGO 提供了两个金融函数。

1）@fpa(I,n)

返回如下情形的净现值：单位时段利率为 I，连续 n 个时段支付，每个时段支付单位费用。若每个时段支付 x 单位的费用，则净现值可用 x 乘以@fpa(I,n)算得。@fpa 的
计算公式为:

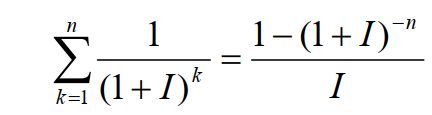
其中，净现值就是在一定时期内为了获得一定收益在该时期初所支付的实际费用。
eg. （贷款买房问题）贷款金额 50000 元，贷款年利率 5.31%，采取分期付款方式（每年年末还固定金额，直至还清）。问拟贷款 10 年，每年需偿还多少元？
LINGO 代码如下：
50000 = x * @fpa(.0531,10);
答案是 x=6573.069 元。

2)@fpl(I,n)

返回如下情形的净现值：单位时段利率为 I，第 n 个时段支付单位费用。@fpl(I,n)的计算公式为;

这两个函数间的关系为：

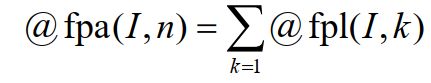
4、概率函数

1）@pbn(p,n,x)：二项分布的累积分布函数。
2）@pcx(n,x)：自由度为 n 的 χ 2 分布的累积分布函数。
3）@peb(a,x)：当到达负荷为 a，服务系统有 x 个服务器且允许无穷排队时的 Erlang 繁忙概率。
4）@pel(a,x)：当到达负荷为 a，服务系统有 x 个服务器且不允许排队时的 Erlang 繁忙概率。
5）@pfd(n,d,x)：自由度为 n 和 d 的 F 分布的累积分布函数。
6）@pfs(a,x,c)：当负荷上限为 a，顾客数为 c，平行服务器数量为 x 时，有限源的 Poisson 服务系统的等待或返修顾客数的期望值。 a 是顾客数乘以平均服务时间， 再除以平均返修时间。当 c 和（或）x 不是整数时，采用线性插值进行计算。
7）@phg(pop,g,n,x)：超几何（Hypergeometric）分布的累积分布函数。pop 表示产品总数，g 是正品数。从所有产品中任意取出 n（n≤pop）件。pop，g，n 和 x 都可以是非整数，这时采用线性插值进行计算。
8）@ppl(a,x)：Poisson 分布的线性损失函数，即返回 max(0,z-x)的期望值，其中随机变量 z 服从均值为 a 的 Poisson 分布。
9）@pps(a,x)：均值为 a 的 Poisson 分布的累积分布函数。当 x 不是整数时，采用线性插值进行计算。
10）@psl(x)：单位正态线性损失函数，即返回 max(0,z-x)的期望值，其中随机变量 z 服从标准正态分布。
11）@psn(x)：标准正态分布的累积分布函数。
12）@ptd(n,x)：自由度为 n 的 t 分布的累积分布函数。
13）@qrand(seed)：产生服从(0,1)区间的拟随机数。@qrand 只允许在模型的数据部分使用，它将用拟随机数填满集属性。通常，声明一个 m×n 的二维表，m 表示运行实验的次数，n 表示每次实验所需的随机数的个数。**在行内，随机数是独立分布的；在行间，随机数是非常均匀的。**这些随机数是用“分层取样”的方法产生的。
14）@rand(seed)：返回 0 和 1 间的伪随机数，依赖于指定的种子。典型用法是 U(I+1)=@rand(U(I))。
注意：如果 seed 不变，那么产生的随机数也不变。

下面看一个具体应用的例子：利用@rand 产生 15 个标准正态分布的随机数和自由度为 2 的 t 分布的随机数。
model:
!产生一列正态分布和 t 分布的随机数;
sets:
series/1…15/: u, znorm, zt;
endsets
!第一个均匀分布随机数是任意的;
u(1) = @rand( .1234);
!产生其余的均匀分布的随机数;
@for(series(I)|I #GT# 1:u(I)=@rand(u(I-1)));
@for(series( I):
!正态分布随机数;
@psn(znorm(I))=u(I);
!和自由度为 2 的 t 分布随机数;
@ptd(2,zt(I))=u(I);
!ZNORM 和 ZT 可以是负数;
@free(znorm(I)); @free(zt(I)));
end

5、变量界定函数

变量界定函数实现对变量取值范围的附加限制，共 4 种：

1）@bin(x)

限制 x 为 0 或 1；

2）@bnd(L,x,U)

限制 L≤x≤U；

3）@free(x)

取消对变量 x 的默认下界为 0 的限制，即 x 可以取任意实数；

4）@gin(x)

限制 x 为整数。
在默认情况下，LINGO 规定变量是非负的，也就是说下界为 0，上界为+∞。@free取消了默认的下界为 0 的限制，使变量也可以取负值。@bnd 用于设定一个变量的上下界,它也可以取消默认下界为 0 的约束。

6、 集操作函数

1）@in(set_name,primitive_index_1 [,primitive_index_2,…])

如果元素在指定集中，返回 1；否则返回 0。其中set_name表示集合的名称，primitive_index表示该集合所涉及的原始父集的索引，可能有多个，primitive_index的值也可由@index（）函数给出。
例如：全集为 I，B 是 I 的一个子集，C 是 B 的补集。
sets:
I/x1…x4/:x;
B(I)/x2/:y;
C(I)|#not#@in(B,&1):Z;
endsets
总结：此处集合B、C均是派生集合。

2）@index([set_name,] primitive_set_element)

该函数返回在集 set_name 中原始集成员primitive_set_element 的索引。如果set_name 被忽略，那么 LINGO 将返回与 primitive_set_element 匹配的第一个原始集成员的索引。如果找不到，则产生一个错误。
例 如： 如何确定集成员(B,Y)属于派生集 S3？
sets:
S1/A B C/;
S2/X Y Z/;
S3(S1,S2)/A X, A Z, B Y, C X/;
endsets
X=@in(S3,@index(S1,B),@index(S2,Y));
若上面的程序运行后，X=1则说明集成员（B,Y）属于S3,若X=0，则不属于，本例X=1.
看下面的例子，表明有时为@index 指定集是必要的。
sets:
girls/debble,sue,alice/;
boys/bob,joe,sue,fred/;
endsets
I1=@index(sue);
I2=@index(boys,sue);
I1 的值是 2，I2 的值是 3。由于在I1=@index(sue)中set_name 被忽略，那么 LINGO 返回与 primitive_set_element 匹配的第一个原始集，即girls集合，此时I1 的值是 2。而I2=@index(boys,sue)中指定了集合boys,所以I2 的值是 3。因此：成员的索引建议在使用@index 函数时最好指定集。

3）@wrap(index,limit)

该函数返回 j=index-klimit，其中 k 是一个整数，取适当值保证 j 落在区间[1，limit]内。该函数在循环、多阶段计划编制中特别有用。
即当给定一个数X时，若X属于区间[1，limit]，则返回X值，若X＞limit,则返回mod(X,limit)的值。一般的，该函数返回 j=index-klimit，其中 k 是一个整数，取适当值保证 j 落在区间[1，limit]内。

4)@size(set_name)

该函数返回集 set_name 的成员个数。 在模型中明确给出集大小时最好使用该函数。它的使用使模型更加数据中立，集大小改变时也更易维护。

7、 集循环函数

集循环函数遍历整个集进行操作。
语法格式：
@function(setname[(set_index_list)[|conditional_qualifier]]:
expression_list);
@function 相应于下面罗列的四个集循环函数之一；
setname 是要遍历的集；
set_index_list 是集索引列表；
conditional_qualifier 是用来限制集循环函数的范围，当
集循环函数遍历集的每个成员时，LINGO 都要对 conditional_qualifier 进行评价，若结果为真，则对该成员执行@function 操作，否则跳过，继续执行下一次循环。
expression_list 是被应用到每个集成员的表达式列表。
*注意：当用的是@for 函数时，expression_list 可以包含多个表达式，其间用逗号隔开。这些表达式将被作为约束加到模型中。当使用其余的三个集循环函数时，expression_list 只能有一个表达式。*如果省略 set_index_list，那么在 expression_list 中引用的所有属性的类型都属于setname 集。

1）@for

该函数用来产生对集成员的约束。基于建模语言的标量需要显式输入每个约束，不过@for 函数允许只输入一个约束，然后 LINGO 自动产生每个集成员的约束。
例 如：产生序列{1,4,9,16,25}
model:
sets:
number/1…5/:x;
endsets
@for(number(I): x(I)=I^2);
end

2）@sum

该函数返回遍历指定的集成员的一个表达式的和。
例 如：求向量[5，1，3，4，6，10]前 5 个数的和。
model:
data:
N=6;
enddata
sets:
number/1…N/:x;
endsets
data:
x = 5 1 3 4 6 10;
enddata
s=@sum(number(I) | I #le# 5: x);
end

3）@min 和@max

返回指定的集成员的一个表达式的最小值或最大值。
例 如： 求向量[5，1，3，4，6，10]前 5 个数的最小值，后 3 个数的最大值。
model:
data:
N=6;
enddata
sets:
number/1…N/:x;
endsets
data:
x = 5 1 3 4 6 10;
enddata
minv=@min(number(I) | I #le# 5: x);
maxv=@max(number(I) | I #ge# N-2: x);
end

8、 输入和输出函数

1）@file 函数

该函数用从外部文件中输入数据，可以放在模型中任何地方。该函数的语法格式为@file(’filename’)。这里 filename 是文件名，可以采用相对路径和绝对路径两种表示方式。
注意：在 LINGO 中不允许嵌套调用@file 函数，文本文件记录之间用“~”隔开。

2）@text 函数

该函数被用在数据部分用来把解输出至文本文件中。它可以输出集成员和集属性值。其语法为@text([’filename’])，这里 filename 是文件名，可以采用相对路径和绝对路径两种表示方式。
注意：@text([’filename’])一般出现在一条语句的左边。语句的右边为集名（用来输出该集的所有成员名）或集属性名（用来输出该集属性的值）。

3）@ole 函数

@OLE 是从 EXCEL 中引入或输出数据的接口函数，它是基于传输的 OLE 技术。

9 、结果报告函数

1）@WRITE(obj1[,…,objn])

这个函数只能在数据段中使用，用于输出一系列结果（obj1, …,objn），其中obj1, …,objn 等可以是变量（但不能只是属性），也可以是字符串（放在单引号中的为字符串）或换行（@NEWLINE(1)）等。 结果可以输出到一个文件， 或电子表格（如 Excel），或数据库，这取决于@WRITE 所在的输出语句中左边的定位函数。例如：
DATA:
@TEXT()=@WRITE(’A is ’,A,’,B is ’,B,’,A/B is’,A/B);
ENDDATA
其中 A，B 是模型中的变量，则上面语句的作用是在屏幕上输出 A，B 以及 A/B 的值，其中此处加入的字符串是为了使结果更便于阅读。假设计算结束时 A=10，B=5，则输出为
A is 10, B is 5, A/B is 2

2）@WRITEFOR(setname[(set_index_list)[|condition]]:obj1[,objn])

这个函数可以看作是函数@WRITE 在循环情况下的推广，它输出集合上定义的属性。

3）@ITERS()

这个函数只能在程序的数据段使用，调用时不需要任何参数，总是返回 LINGO 求解器计算所使用的总迭代次数。例如：
@TEXT()=@WRITE('Iterations= ',@ITERS());
将迭代次数显示在屏幕上。

4）@NEWLINE(n)

这个函数在输出设备上输出 n 个新行（n 为一个正整数）。

5）@STRLEN(string)

这个函数返回字符串“string”的长度，如@STRLEN(123)返回值为 3。

6）@NAME(var_or_row_reference)

这个函数返回变量名或行名。

7）符号 *

在@write 和@writefor 函数中，可以使用符号* 表示将一个字符串重复多次，用法是将 *放在一个正整数 n 和这个字符串之间，表示将这个字符串重复 n 次。

8）@format(value,format_descriptor)

在@write 和@writefor 函数中，可以使用@format 函数对数值设定输出格式。其中，value 表示要输出的数值，而 format_descriptor（格式描述符）表示输出格式。

9）@ranged(variable_or_row_name)

为了保持最优基不变，变量的费用系数或约束行的右端项允许减少的量。

10）@rangeu(variable_or_row_name)

为了保持最优基不变，变量的费用系数或约束行的右端项允许增加的量。

11）@status()

返回 LINGO 求解模型结束后的状态：
0 Global Optimum（全局最优）
1 Infeasible（不可行）
2 Unbounded（无界）
3 Undetermined（不确定）
4 Feasible（可行）
5 Infeasible or Unbounded（通常需要关闭“预处理”选项后重新求解模型，以确定模型究竟是不可行还是无界）
6 Local Optimum（局部最优）
7 Locally Infeasible（局部不可行，尽管可行解可能存在，但是 LINGO 并没有找到一个）
8 Cutoff（目标函数的截断值被达到）
9 Numeric Error（求解器因在某约束中遇到无定义的算术运算而停止）通常，如果返回值不是 0、4 或 6 时，那么解将不可信，几乎不能用。该函数仅被用在模型的数据部分来输出数据。

12）@dual

@dual(variable_or_row_name)返回变量的判别数（检验数）或约束行的对偶（影子）价格（dual prices）。

10、 辅助函数

1）@if(logical_condition,true_result,false_result)

@if 函数将评价一个逻辑表达式 logical_condition，如果为真，返回 true_result，否则返回 false_result。

2）@warn(’text’,logical_condition)

如果逻辑条件 logical_condition 为真，则产生一个内容为’text’的信息框。