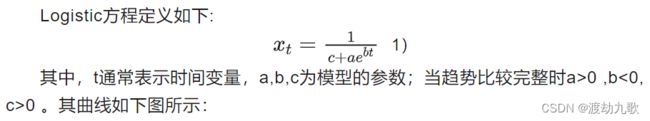数学建模-Logistic模型附Matlab代码

目录

一、Logistic模型介绍

二、Logistic模型实例

三、Logistic模型原理

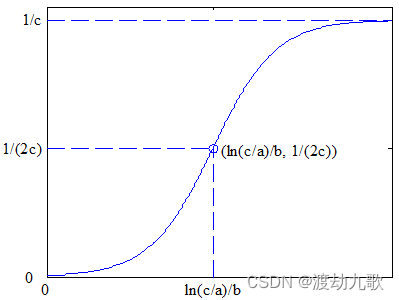
3.1 Logistic 方程定义

3.2 Yule算法

3.2 Rhodes算法

3.3 Nair算法 

4、Logistic模型Matlab部分代码

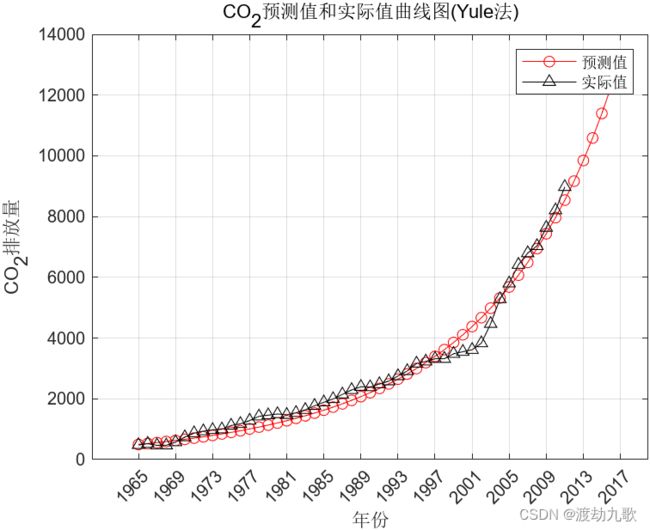
4.1 Yule算法

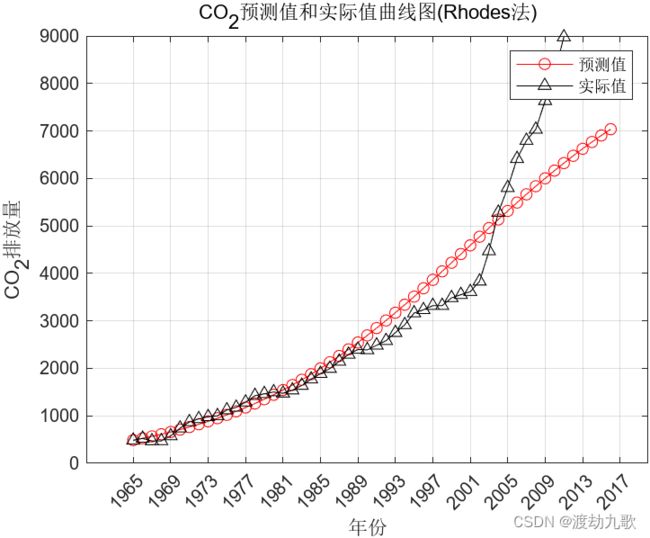
4.2 Rhodes算法

4.3 Nair算法

一、Logistic模型介绍

       logistic回归又称logistic回归分析，是一种广义的线性回归分析模型，常用于数据挖掘，疾病自动诊断，经济预测等领域。例如，探讨引发疾病的危险因素，并根据危险因素预测疾病发生的概率等。以胃癌病情分析为例，选择两组人群，一组是胃癌组，一组是非胃癌组，两组人群必定具有不同的体征与生活方式等。因此因变量就为是否胃癌，值为“是”或“否”，自变量就可以包括很多了，如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的，也可以是分类的。然后通过logistic回归分析，可以得到自变量的权重，从而可以大致了解到底哪些因素是胃癌的危险因素。同时根据该权值可以根据危险因素预测一个人患癌症的可能性。

二、Logistic模型实例

       江苏省1965-2011年全过程建筑碳排放量（单位：万吨）如下表。用logistic方程模拟江苏省C全过程建筑排放量的变化趋势，分别用不同的方法估计方程参数，并分别计算三种方法的MAPE及未来五年全过程建筑排放量的预测结果。

1965	1966	…	2010	2011
480.9	522.0	…	8209.8	8979.1

三、Logistic模型原理

3.1 Logistic 方程定义

 

3.2 Yule算法

由3.1公式一推得：

 3.2 Rhodes算法

3.3 Nair算法 

4、Logistic模型Matlab部分代码

4.1 Yule算法

clear;clc;
%Yule算法：
X=[480.9,522,468.8,469.5,573.8,737.8,869.8,933.7,977.2,...
    997.7,1120.3,1176.1,1284.8,1422.1,1462.1,1499.7,...
    1473.1,1539.2,1637,1771,1886.5,1994.6,2145.7,2292,...
    2396.8,2387,2484.4,2580.8,2750.2,2915.7,3163.8,3231.9,...
    3319.5,3319.6,3484.,3550.6,3613.9,3833.1,4471.2,5283,...
    5803.2,6415.5,6797.9,7033.5,7636.3,8209.8,8979.1];

plot(XX(1:length(X)),X,'g-^')
legend('预测值','实际值')
xlabel('年份');ylabel('CO_{2}排放量');
title('CO_{2}预测值和实际值曲线图(Yule法)')
set(gca,'XTick',[1965:4:2017])
grid on
format short;
forecast=YY(end-4:end);%CO2排放量的预测结果
MAPE=sum(abs(YY(1:n+1)-X)./X)/length(X);%平均相对差值
a,b,c

4.2 Rhodes算法

clear;clc;
%Rhodes算法
X=[480.9,522,468.8,469.5,573.8,737.8,869.8,933.7,977.2,...
    997.7,1120.3,1176.1,1284.8,1422.1,1462.1,1499.7,...
    1473.1,1539.2,1637,1771,1886.5,1994.6,2145.7,2292,...
    2396.8,2387,2484.4,2580.8,2750.2,2915.7,3163.8,3231.9,...
    3319.5,3319.6,3484.,3550.6,3613.9,3833.1,4471.2,5283,...
    5803.2,6415.5,6797.9,7033.5,7636.3,8209.8,8979.1];

plot(XX,YY,'r-o')
hold on
plot(XX(1:length(X)),X,'k-^')
set(gca,'XTick',[1965:4:2017])
legend('预测值','实际值')
xlabel('年份');ylabel('CO_{2}排放量');
title('CO_{2}预测值和实际值曲线图(Rhodes法)')
grid on
format short;
forecast=YY(end-4:end);%CO2排放量的预测结果
MAPE=sum(abs(YY(1:n+1)-X)./X)/length(X);%平均相对差值
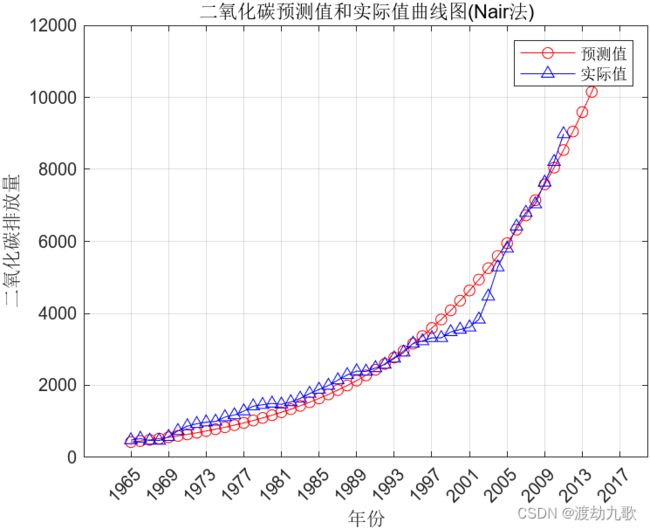
a,b,c

4.3 Nair算法

clear;clc;
%Nair算法
X=[480.9,522,468.8,469.5,573.8,737.8,869.8,933.7,977.2,...
    997.7,1120.3,1176.1,1284.8,1422.1,1462.1,1499.7,...
    1473.1,1539.2,1637,1771,1886.5,1994.6,2145.7,2292,...
    2396.8,2387,2484.4,2580.8,2750.2,2915.7,3163.8,3231.9,...
    3319.5,3319.6,3484.,3550.6,3613.9,3833.1,4471.2,5283,...
    5803.2,6415.5,6797.9,7033.5,7636.3,8209.8,8979.1];
n=length(X)-1;
for t=1:n
    Z(t)=1/X(t)-1/X(t+1);
    S(t)=1/X(t)+1/X(t+1);

hold on
plot(XX(1:length(X)),X,'b-^')
legend('预测值','实际值')
xlabel('年份');ylabel('二氧化碳排放量');
title('二氧化碳预测值和实际值曲线图(Nair法)')
set(gca,'XTick',[1965:4:2017])
grid on
format short;
forecast=YY(end-4:end);%CO2排放量的预测结果
MAPE=sum(abs(YY(1:n+1)-X)./X)/length(X);%平均相对差值
a,b,c