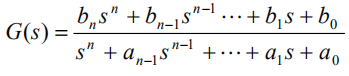状态空间模型与传递函数的转换关系+例题
目录
- 一、传递函数 → \rightarrow →状态空间模型
-
- 1.1 预处理
- 1.2 从最简单的分子为1的传递函数入手
- 1.3 分子不为1的传递函数
- 1.4 另一种思路:利用线性叠加原理
- 1.5 对复杂系统使用分解法
-
- 1.5.1 串联法
- 1.5.2 并联法
- 二、状态空间模型 → \rightarrow →传递函数
- 三、对偶关系
- 四、例题
- 五、参考资料
传递函数是经典控制理论的工具,只能用于SISO和LTI系统;状态空间模型属于现代控制理论,对SISO和MIMO、LTI和非线性或时变系统都适用。既然考虑二者的互相转换,那么对象只可能是满足SISO和LTI的系统。
一、传递函数 → \rightarrow →状态空间模型
1.1 预处理
用长除法进行简化:

从而得到新的G(s):
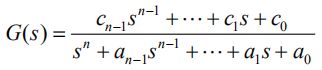
原来的G(s)是新的G(s)和d的并联,可以按并联系统处理。方便起见,下面先只考虑形似新的G(s)的传递函数。
1.2 从最简单的分子为1的传递函数入手
一个例子:
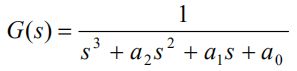
要求它的状态空间模型,首先写成输入输出关系:
![]()
对应的微分方程:
![]()
定义新的变量:
![]()
状态空间模型:

状态矩阵A:最底行对应传递函数分母的系数,符号相反;右上角是2阶单位阵。
输入矩阵B:只有最后一维非零,对应分子常数1。
输出矩阵C:只有第一维非零,1对应分子常数1。
直接转移矩阵D:为0,因为G(s)的分子次数小于分母。
模拟图:
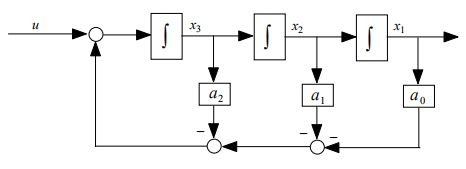
画的时候左边是u,根据B中只有第三维是1,确定u通过加法流向 x 3 ˙ \dot{x_3} x3˙,积分得到 x 3 x_3 x3。然后再画 x 2 ˙ , x 2 , x 1 ˙ , x 1 \dot{x_2},x_2,\dot{x_1},x_1 x2˙,x2,x1˙,x1。根据 x 3 ˙ \dot{x_3} x3˙的构成画反馈。根据C得到 y = x 1 y=x_1 y=x1。
根据前面找到的规律,把上面的三阶传递函数,推广到一般情况:

对应的状态空间模型是

称为是传递函数G的状态空间实现。
1.3 分子不为1的传递函数
还是考虑分母是三阶的:

可以看成是:

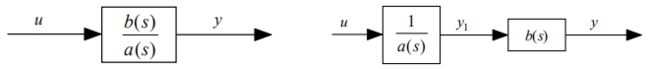
对于内层
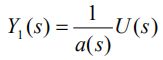
的部分,显然

对于外层
![]()
微分方程:
![]()
定义状态变量:
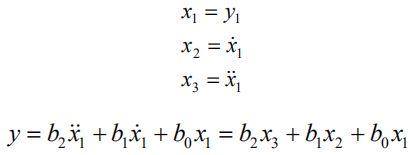
这里的 y 1 y_1 y1也就是分子为1时候的y。也就是说,分子不为1的时候,输出是原来y及其微分的线性组合。所以,对于分子不为1的传函,状态空间模型是
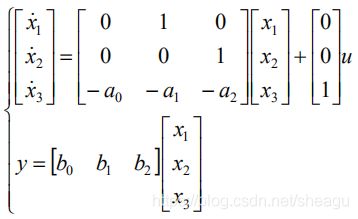
4个矩阵中只有C发生了变化:与传递函数的分子系数相对应。
相应的图为:
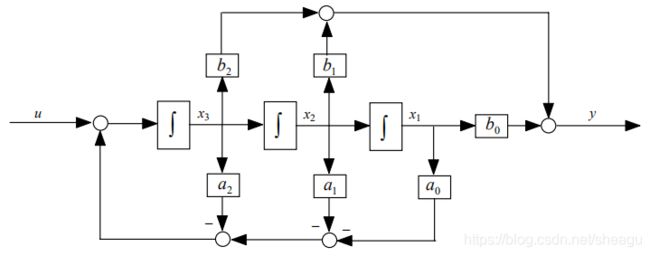
画的时候,将3个积分器的输出线性相加得到最后的输出。
仍然把3维的推广到n维,并且考虑长除法得到的商:
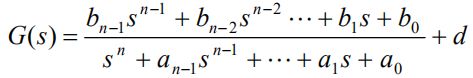
对应的状态空间模型为:

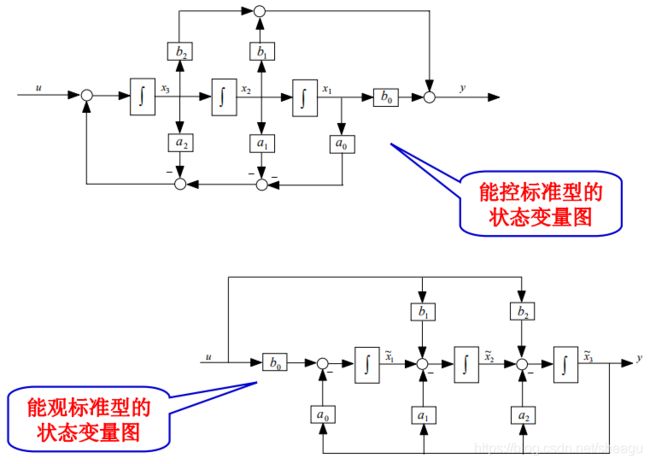
只要把G化成上面的形式,就可以直接观察系数写出模型的4个矩阵了,很方便。这个形式的模型称为“能控标准型”。
1.4 另一种思路:利用线性叠加原理
还是以3阶系统为例:

如果直接写成y和u的微分方程:
![]()
这时候,右边的u是有微分项的(而按1.2中的方法,由于内层的分子是1,避免了这个问题)。
如果先不看微分项,只考虑

它和前面分析过的分子为1的传递函数是一样的,即有
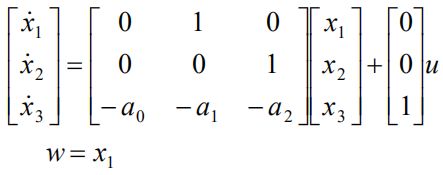
然后只考虑u的一阶微分项作为输入:
![]()
对比上一个方程,可以发现这个方程是上一个方程两边再做一次微分的结果,所以输出分量r和w有这样的关系:
![]()
同理,只考虑u的二阶微分的时候:
![]()
又满足:
![]()
根据叠加原理,总的输出是3个输入分量得到的3个输出分量的线性和:

b对应y-u微分方程右边的系数。
1.5 对复杂系统使用分解法
如果G的阶数比较高,可以把它分解成低阶的,先得到低阶的状态空间模型,再合成高阶的模型。可以用串联法、并联法等。
1.5.1 串联法
有的传递函数很容易因式分解,可以用串联法,例如:

因式分解:
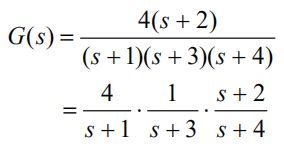
看成是三个环节的串联,很容易得到它们各自的模型:

系数的求法用之前的方法就可以做,前两个环节由于阶数很低,熟练之后可以直接看出来。对于第三个环节,我们可以设 X 3 ( s ) = 1 s + 4 U 3 ( s ) X_3(s)=\frac{1}{s+4}U_3(s) X3(s)=s+41U3(s)而 Y ( s ) = ( s + 2 ) X 3 ( s ) Y(s)=(s+2)X_3(s) Y(s)=(s+2)X3(s),即可得:
x ˙ 3 = − 4 x 3 + u 3 y = x ˙ 3 + 2 x 3 = − 4 x 3 + u 3 + 2 x 3 = − 2 x 3 + u 3 \begin{aligned} \dot{x}_3&=-4x_3+u_3\\ y&=\dot{x}_3+2x_3\\ &=-4x_3+u_3+2x_3\\ &=-2x_3+u_3 \end{aligned} x˙3y=−4x3+u3=x˙3+2x3=−4x3+u3+2x3=−2x3+u3
这三个环节有什么关联呢?u2=y1,u3=y2。所以
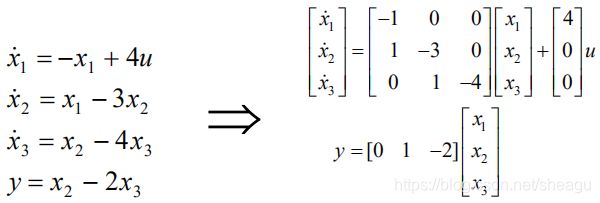
图:

1.5.2 并联法
考虑
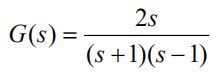
分解得到
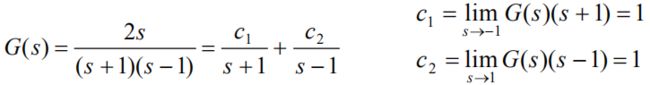
画图,分别求出两个环节的模型:

对于并联,两个环节之间的关系是:u=u1=u2,y=y1+y2。因此
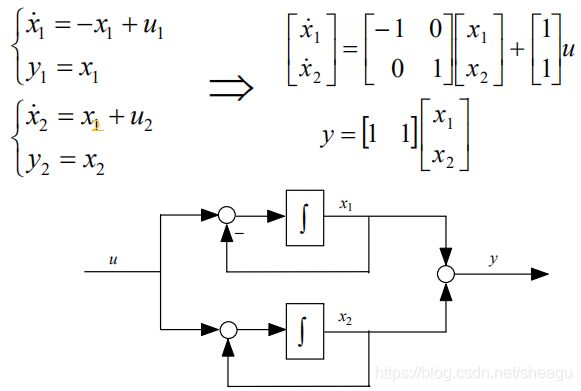
这里的A是对角阵,所以并联得到的也称“对角型”。
系数的规律:
A中的系数值是传递函数极点-1和1,B的系数对应分子1和1。
实际上,对于
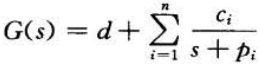
利用并联法得到的模型为:

状态图:
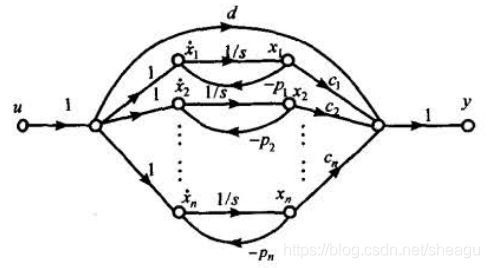
如果存在重极点,例如:

系数用留数定理求:

输入输出关系为:
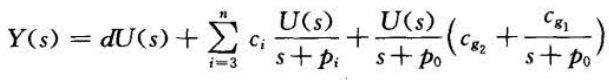
令
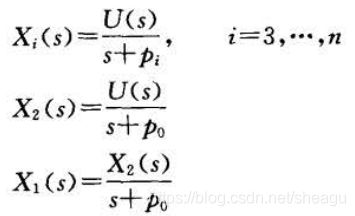
得到系统状态方程和输出方程:
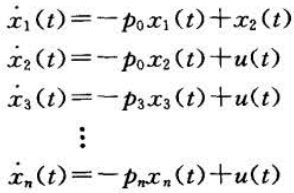
![]()
因此,模型为:

观察发现,如果存在重根,则A为若当型,n重根对应的若当块是n阶的,并且相应的B中的系数为0。
状态图为:
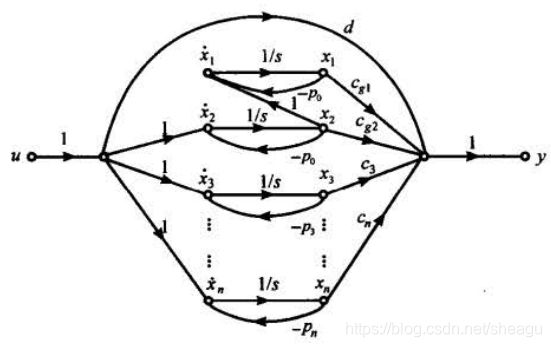
二、状态空间模型 → \rightarrow →传递函数
设已知的状态空间模型为:
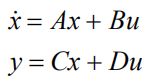
在零初始条件下,用拉普拉斯变换得到
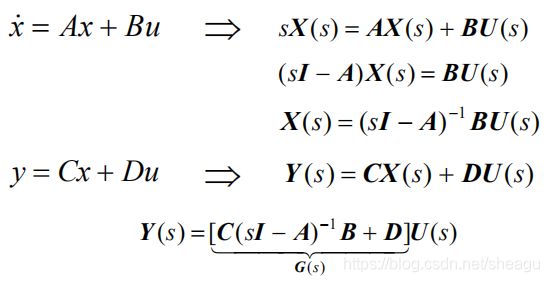
所以
![]()
可见,传递函数是由状态空间模型唯一确定的。
三、对偶关系
在2中根据状态空间模型可以求出传递函数:
![]()
对于SISO系统,这是一个标量,所以, G = G T G=G^T G=GT。由此,可以得到:
![]()
这两种写法的形式是一样的,对比系数可以得出另一种模型写法:
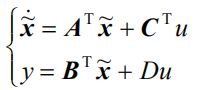
这种写法的模型被称为原来模型的对偶系统模型。
对这个对偶模型再做一次对偶,可以得到原来的模型
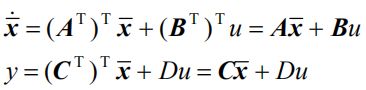
这说明对偶关系是双向的,它们互为对偶。
我们上面写过能控标准型:
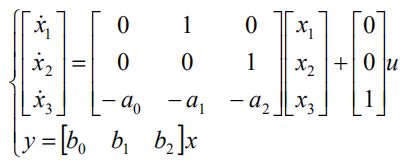
它也有它的对偶模型,即“能观标准型”:
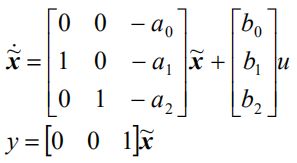
两种模型的状态图:
四、例题
五、参考资料
[1] 浙江工业大学俞立老师课程ppt,网课见b站:现代控制理论 浙江工业大学 俞立,评论区有ppt的网盘链接
[2] 田玉平,蒋珉,李世华.自动控制原理[M].北京:科学出版社,2006