算法期末复习-----递归与分治
第二章递归与分治
直接或间接地调用自身的算法称为递归算法。用函数自身给出定义的函数称为递归函数。
1.全排列
算法思想:当n=1时,Perm(R)=(r),当n>1时,perm (R)=(r1)perm(R1),Ri=R-{ri),而perm(R1)=(r2)perm(R2),perm (R2)=(r3)perm(R3).....................perm(list,k,m)递归的地产生所有前缀是list[0:k-1],且后缀是list[k:m]的全排列的所有排列。调用算法perm(list,0,m-1)则产生list[0:n-1]的全排列。
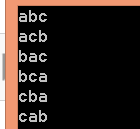
例如:abc
一、交换a a
以a为前缀,求bc的全排列----以b为前缀,求c的全排列----得到abc
交换b c
----以c为前缀,求b的全排列----得到acb
二、交换a b
以b为前缀,求ac的全排列----以a为前缀,求c的全排列----得到bac
交换a c
----以c为前缀,求a的全排列----得到bca
三、交换a c
以c为前缀,求ba的全排列----以b为前缀,求a的全排列----得到cba
交换b a
----以a为前缀,求b的全排列----得到cab
#include
void swap(char* a,char* b){
char c;
c=*a;
*a=*b;
*b=c;
}
void perm(char* list,int k,int m){
if(k==m){
for(int i=0;i<=m;i++){
printf("%c",list[i]);
}
printf("\n");
}else{
for(int i=k;i<=m;i++){
swap(&list[k],&list[i]);
perm(list,k+1,m);
swap(&list[k],&list[i]);
}
}
}
int main(){
char list[4]={'a','b','c'};
perm(list,0,2);
return 0;
} 2.整数划分
对正整数的不同划分中,将最大加数n1不大于m的划分个数记为q(n,m)。n代表整数n,m代表最大加数。
由此可建立递归关系
6; q(6,6)=q(6,5)+1
5+1; =q(6,4)+q(1,5)+1
4+2,4+1+1; =q(6,3)+q(2,4)+q(1,5)+1
3+3,3+2+1,3+1+1+1; =q(6,2)+q(3,3)+q(2,4)+q(1,5)+1
2+2+2,2+2+1+1,2+1+1+1+1; =q(6,1)+q(4,2)+q(3,3)+q(2,4)+q(1,5)+1
1+1+1+1+1+1。
q(6,6)=11 即代表整数6,最大加数小于等于6的划分
q(6,5)=10 即代表整数6,最大加数小于等于5的划分
q(6,4)=9 即代表整数6,最大加数小于等于4的划分,即标蓝部分。
递归方程:
#include
int q(int n,int m){
if(n==1||m==1)
return 1;
else if(m>n)
return q(n,n);
else if(m==n)
return q(n,n-1)+1;
else if(n>m)
return q(n-m,m)+q(n,m-1);
}
int main(){
int n;
while(~scanf("%d",&n)){
int res=q(n,n);
printf("%d\n",res);
}
return 0;
} 3.汉诺塔
三个柱子要求从1号移动到2号,辅助柱子3号,规则:每次只能移动一个盘子,任何时刻都不允许将较大的圆盘压到较小的圆盘上。
算法思想:
n个圆盘的移动问题可分为两次n-1个圆盘的移动问题,即将n-1个圆盘借助2号从1号移到3号,再将第n个圆盘从1号移动到2号,再将n-1个圆盘借助1号从3号移到2号。
#include
//n为盘子总数,a为起始盘子,b为终点盘子,c为辅助盘子
int count=0;
void move(int n,int a,int b){
count++;
printf("%d号盘子从%d柱子--->%d柱子\n",n,a,b);
}
void hanoi(int n,int a,int b,int c){
if(n==1)
move(1,a,b);
if(n>1){
hanoi(n-1,a,c,b);
move(n,a,b);//若不跟踪每个盘子的移动,则move(a,b)
hanoi(n-1,c,b,a);
}
}
int main(){
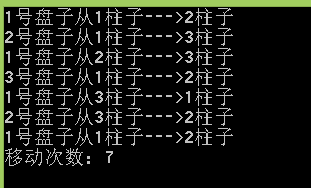
hanoi(3,1,2,3);//把盘子从上到下编号1-n,把n个盘子从1号柱子移到2号柱子
printf("移动次数:%d\n",count);
return 0;
}
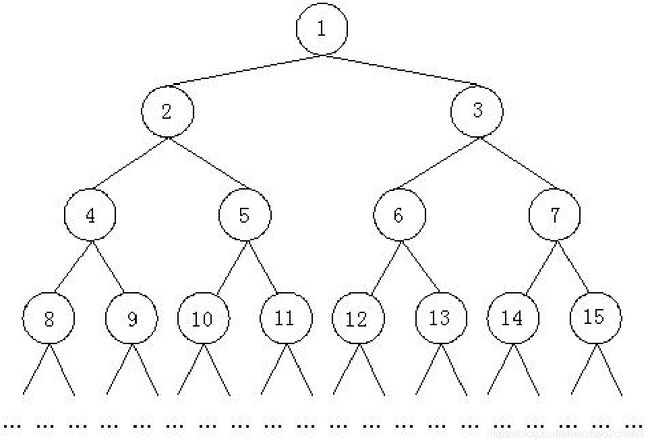
4.要求二叉树上任意两个节点的最近公共子节点
解题思路
这个题目要求树上任意两个节点的最近公共子节点。分析这棵树的结构不难看出,不论奇数偶数,每个数对2做整数除法,就走到它的上层结点。
我们可以每次让较大的一个数(也就是在树上位于较低层次的节点)向上走一个结点,直到两个结点相遇。如果两个节点位于同一层,并且它们不相等,可以让其中任何一个先往上走,然后另一个再往上走,直到它们相遇,
设common(x, y) 表示整数x和y的最近公共子节点,那么,根据比较x 和y 的值,我们得到三种情况:
x = y,则common(x, y)=x =y
x > y,则common(x, y)=common(x/2, y)
x < y,则common(x, y)=common(x, y/2)
#include
int common(int x,int y){
if(x==y)
return x;
if(x>y)
return common(x/2,y);
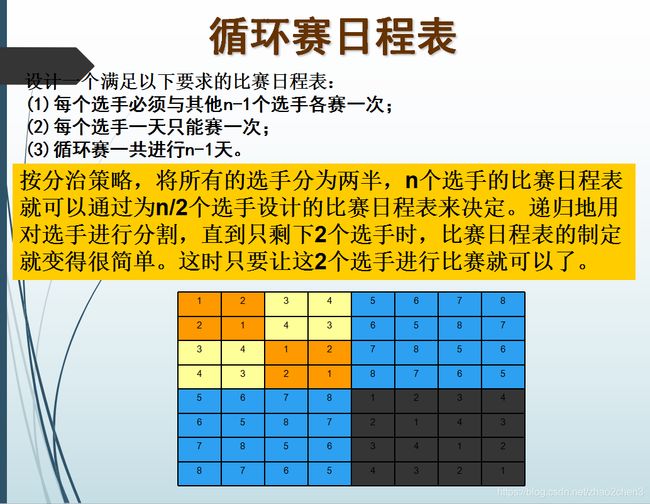
if(x 分治
分治法所能解决的问题一般具有以下几个特征:
1.该问题的规模缩小到一定的程度就可以容易地解决;(因为问题的计算复杂性一般是随着问题规模的增加而增加,因此大部分问题满足这个特)
2.该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质(这条特征是应用分治法的前提,它也是大多数问题可以满足的,此特征反映了递归思想的应用)
3.利用该问题分解出的子问题的解可以合并为该问题的解;(能否利用分治法完全取决于问题是否具有这条特征,如果具备了前两条特征,而不具备第三条特征,则可以考虑贪心算法或动态规划。)
4.该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。(这条特征涉及到分治法的效率,如果各子问题是不独立的,则分治法要做许多不必要的工作,重复地解公共的子问题,此时虽然也可用分治法,但一般用动态规划较好。)
二分搜索技术
先排序
基本思想:将n个元素分成个数大致相同的两半,取a[n/2]与x进行比较,如果x=a[n/2],则找到x,算法终止。如果x
//查找下标
#include
#include
using namespace std;
int binarySearch(int* a,int x,int n){
int left=0,right=n-1;
while(left<=right){
int middle=(left+right)/2;
if(x==a[middle])
return middle;
if(x<=a[middle])
right=middle-1;
if(x>=a[middle])
left=middle+1;
}
}
int main(){
int a[10]={1,5,3,2,9,22,8,23,36,90};
sort(a,a+10);
printf("%d\n",binarySearch(a,36,10));
return 0;
} 算法复杂度分析:
每执行一次算法的while循环, 待搜索数组的大小减少一半。因此,在最坏情况下,while循环被执行了O(logn) 次。循环体内运算需要O(1) 时间,因此整个算法在最坏情况下的计算时间复杂性为O(logn) 。
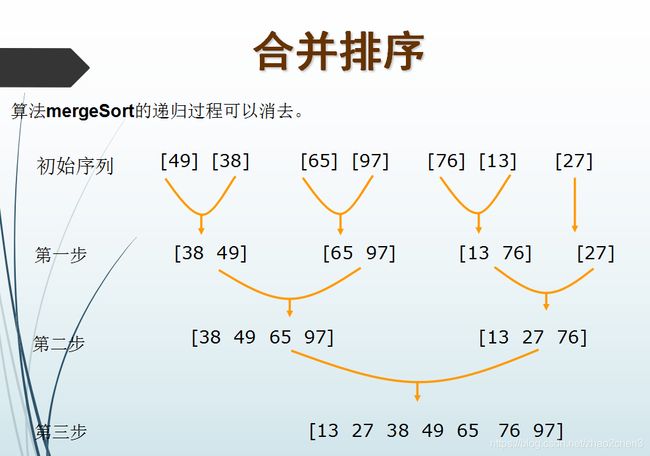
合并排序
基本思想:将待排序元素分成大小大致相同的2个子集合,分别对2个子集合进行排序,最终将排好序的子集合合并成为所要求的排好序的集合。
分治策略基本思想:将原问题划分成n个规模较小而结构与原问题相似的小问题;递归地解决这些子问题,然后再合并其结果,就得到原问题的解。
分治模式在每一层递归上都有三个步骤;
分解(Divide):将原问题分解成这一系列子问题。
解决(Conquer):递归地解各子问题。若子问题足够小,则直接求解。
合并(Combine):将子问题的结果合并成原问题的解。
合并排序算法完全依照了上述模式,直观地操作如下:
分解:将n个元素分成各含n/2个元素的子序列;
解决:用合并排序法对两个子序列递归地排序;
合并:合并两个已排序的子序列以得到排序结果;
public static void mergeSort(Comparable a[], int left, int right)
{
if (left快速排序
快速排序基本思想
快速排序采用了一种分治的策略,通常称其为分治法,其基本思想是:将原问题分解为若干个规模更小但结构与原问题相似的子问题。递归地解这些子问题,然后将这些子问题的解组合为原问题的解。
1、先从数列中取出一个数作为基准数。
2、分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
3、再对左右区间重复第二步,直到各区间只有一个数。
快速排序步骤
1、设置两个变量I、J,排序开始的时候:I=0,J=N-1;
2、以第一个数组元素作为关键数据,赋值给key,即 key=A[0];
3、从J开始向前搜索,即由后开始向前搜索(J=J-1),找到第一个小于key的值A[J],并与A[I]交换;
4、从I开始向后搜索,即由前开始向后搜索(I=I+1),找到第一个大于key的A[I],与A[J]交换;
5、重复第3、4、5步,直到 I=J; (3,4步是在程序中没找到时候j=j-1,i=i+1,直至找到为止。找到并交换的时候i, j指针位置不变。另外当i=j这过程一定正好是i+或j-完成的最后另循环结束。)
6、采用同样的方法,对左边的组和右边的组进行排序,直到所有记录都排到相应的位置为止。
初始关键数据:X=49,注意关键X永远不变,永远是和X进行比较,无论在什么位子,最后的目的就是把X放在中间,小的放前面大的放后面。
最坏时间复杂度:O(n2)
平均时间复杂度:O(nlogn)
辅助空间:O(n)或O(logn)
稳定性:不稳定
#include
using namespace std;
void Qsort(int a[], int low, int high)
{
if(low >= high)
{
return;
}
int first = low;
int last = high;
int key = a[first];/*用字表的第一个记录作为枢轴*/
while(first < last)
{
while(first < last && a[last] >= key)
{
--last;
}
a[first] = a[last];/*将比第一个小的移到低端*/
while(first < last && a[first] <= key)
{
++first;
}
a[last] = a[first];
/*将比第一个大的移到高端*/
}
a[first] = key;/*枢轴记录到位*/
Qsort(a, low, first-1);
Qsort(a, first+1, high);
}
int main()
{
int a[] = {49,38,65,97,76,13,27};
Qsort(a, 0, sizeof(a) / sizeof(a[0]) - 1);/*这里原文第三个参数要减1否则内存越界*/
for(int i = 0; i < sizeof(a) / sizeof(a[0]); i++)
{
cout << a[i] << " ";
}
return 0;
}/*参考数据结构p274(清华大学出版社,严蔚敏)*/