图文证明 等价无穷小替换
等价无穷小替换
定义
等价无穷小是无穷小之间的一种关系,指的是:在同一自变量的趋向过程中,若两个无穷小之比的极限为1,则称这两个无穷小是等价的。无穷小等价关系刻画的是两个无穷小趋向于零的速度是相等的。
设当 x → x 0 时, f ( x ) 和 g ( x ) 均为无穷小量。 \text{设当 } x \to x_0 \text{ 时,} f(x) \text{ 和 } g(x) \text{ 均为无穷小量。} 设当 x→x0 时,f(x) 和 g(x) 均为无穷小量。
若存在正常数 c ,使得 lim x → x 0 f ( x ) g ( x ) = c ,则称 f ( x ) 和 g ( x ) 是等价无穷小量,记作 f ( x ) ∼ g ( x ) 。 \text{若存在正常数 } c \text{,使得 } \lim_{{x \to x_0}} \frac{f(x)}{g(x)} = c \text{,则称 } f(x) \text{ 和 } g(x) \text{ 是等价无穷小量,记作 } f(x) \sim g(x) \text{。} 若存在正常数 c,使得 x→x0limg(x)f(x)=c,则称 f(x) 和 g(x) 是等价无穷小量,记作 f(x)∼g(x)。
通常 c 为 1 , 即 lim x → x 0 f ( x ) g ( x ) = 1 通常c为1,即\lim_{{x \to x_0}} \frac{f(x)}{g(x)} = 1 通常c为1,即x→x0limg(x)f(x)=1
证明
可能有人想,我都无穷小,大家不都是无穷小,不都等价怎么还有那么多等价无穷小的公式?
其实当然是因为他们相等的只是无穷小那一点罢了, 下面我们看例子:
有一个无穷小替换为:
s i n ( x ) ∼ x sin(x) \sim x sin(x)∼x
根据无穷小替换有:
lim x → 0 sin x x = 1 \lim_{{x \to 0}} \frac{\sin x}{x} = 1 x→0limxsinx=1
一看图,其实就能很明显的看出,在0附近,这里很明显可不是在一点处等价 s i n ( x ) ∼ x sin(x) \sim x sin(x)∼x
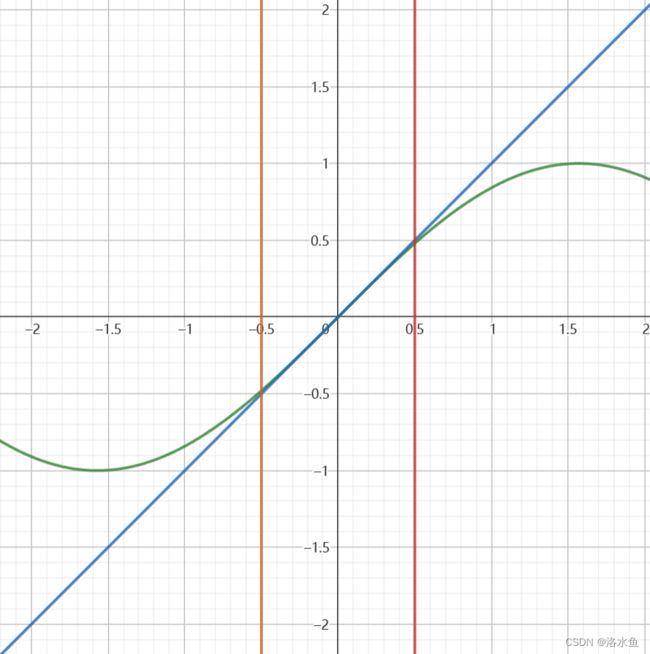
我们来这个的看看:
1 − c o s ( x ) ∼ 1 2 x 2 1-cos(x) \sim \frac {1}{2}x^2 1−cos(x)∼21x2
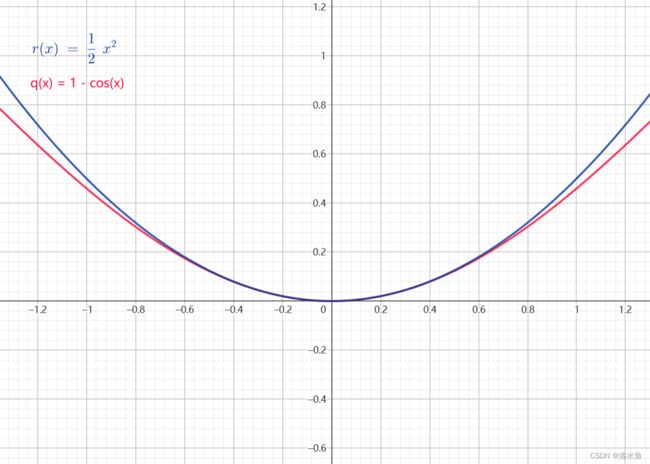
是吧 ! 很明显 ! 有一大段贴合 是吧! 很明显! 有一大段贴合 是吧!很明显!有一大段贴合
我们再来看看合在一起的:

我们可以发现只有等价替换的才会在附近有一大段的贴合,不然就只有无穷小那一点
所以才会有:
lim x → x 0 f ( x ) g ( x ) = 1 \lim_{{x \to x_0}} \frac{f(x)}{g(x)} = 1 x→x0limg(x)f(x)=1
因为趋于0,那一段相当于同一段函数嘛,不是1还是什么
引入泰勒公式证明
详细有关泰勒公式的讲解与证明,请看我的另一篇文章 图文证明 泰勒公式
泰勒和等价无穷本该连在一起认识,才能真正明白等价无穷小替换的本质
这是sin(x)的泰勒展开的一部分:
sin ( x ) = x − x 3 3 ! + x 5 5 ! − x 7 7 ! + … \sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \ldots sin(x)=x−3!x3+5!x5−7!x7+…
根据定义,我们要证明的是:
lim x → 0 s i n ( x ) x = 1 \lim_{{x \to 0}} \frac{sin(x)}{x} = 1 x→0limxsin(x)=1
就能说明二者是等价无穷小
其实很简单,我们只需要将sin(x) 用其泰勒展开替换即可
lim x → 0 x − x 3 3 ! + x 5 5 ! − x 7 7 ! + … x = lim x → 0 x ( 1 − x 2 3 ! + x 4 5 ! − x 6 7 ! + … ) x = lim x → 0 ( 1 − x 2 3 ! + x 4 5 ! − x 6 7 ! + … ) = 1. \begin{aligned} &\lim_{{x \to 0}} \frac{x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \ldots}{x} \\ &= \lim_{{x \to 0}} \frac{x(1 - \frac{x^2}{3!} + \frac{x^4}{5!} - \frac{x^6}{7!} + \ldots)}{x} \\ &= \lim_{{x \to 0}} (1 - \frac{x^2}{3!} + \frac{x^4}{5!} - \frac{x^6}{7!} + \ldots) \\ &= 1. \end{aligned} x→0limxx−3!x3+5!x5−7!x7+…=x→0limxx(1−3!x2+5!x4−7!x6+…)=x→0lim(1−3!x2+5!x4−7!x6+…)=1.
同理
cos ( x ) = 1 − x 2 2 ! + x 4 4 ! − x 6 6 ! + … \cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \ldots cos(x)=1−2!x2+4!x4−6!x6+…
根据定义,我们要证明的是:
lim x → 0 1 − c o s ( x ) 1 2 x 2 = 1 \lim_{{x \to 0}} \frac{1-cos(x)}{\frac {1}{2}x^2} = 1 x→0lim21x21−cos(x)=1
同理代入:
lim x → 0 1 − cos ( x ) 1 2 x 2 = lim x → 0 1 − ( 1 − x 2 2 ! + x 4 4 ! − x 6 6 ! + … ) 1 2 x 2 = lim x → 0 x 2 2 ! − x 4 4 ! + x 6 6 ! − … 1 2 x 2 = lim x → 0 x 2 ( 1 2 ! − x 2 4 ! + x 4 6 ! − … ) 1 2 x 2 = lim x → 0 1 2 ! − x 2 4 ! + x 4 6 ! − … 1 2 = 1. \begin{aligned} &\lim_{{x \to 0}} \frac{1 - \cos(x)}{\frac{1}{2}x^2} \\ &= \lim_{{x \to 0}} \frac{1 - \left(1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \ldots\right)}{\frac{1}{2}x^2} \\ &= \lim_{{x \to 0}} \frac{\frac{x^2}{2!} - \frac{x^4}{4!} + \frac{x^6}{6!} - \ldots}{\frac{1}{2}x^2} \\ &= \lim_{{x \to 0}} \frac{x^2 \left(\frac{1}{2!} - \frac{x^2}{4!} + \frac{x^4}{6!} - \ldots\right)}{\frac{1}{2}x^2} \\ &= \lim_{{x \to 0}} \frac{ \frac{1}{2!} - \frac{x^2}{4!} + \frac{x^4}{6!} - \ldots}{\frac{1}{2}} \\ &= 1. \end{aligned} x→0lim21x21−cos(x)=x→0lim21x21−(1−2!x2+4!x4−6!x6+…)=x→0lim21x22!x2−4!x4+6!x6−…=x→0lim21x2x2(2!1−4!x2+6!x4−…)=x→0lim212!1−4!x2+6!x4−…=1.
再来看看这个求极限:
lim x → 0 x + sin ( x ) x 6 \lim_{{x \to 0}} \frac{{x + \sin(x)}}{{x^6}} x→0limx6x+sin(x)
sin ( x ) = x − x 3 3 ! + x 5 5 ! + . . . \sin(x) = x - \frac{{x^3}}{{3!}} + \frac{{x^5}}{{5!}}+... sin(x)=x−3!x3+5!x5+...
lim x → 0 x + sin ( x ) x 6 = lim x → 0 x + x − x 3 3 ! + x 5 5 ! + . . . x 6 \lim_{{x \to 0}} \frac{{x + \sin(x)}}{{x^6}} = \lim_{{x \to 0}} \frac{{x + x - \frac{{x^3}}{{3!}} + \frac{{x^5}}{{5!}}+...}}{{x^6}} x→0limx6x+sin(x)=x→0limx6x+x−3!x3+5!x5+...
lim x → 0 2 − x 2 3 ! + x 4 5 ! + . . . x 5 \lim_{{x \to 0}} \frac{{2 - \frac{{x^2}}{{3!}} + \frac{{x^4}}{{5!}}+...}}{{x^5}} x→0limx52−3!x2+5!x4+...
lim x → 0 2 x 5 \lim_{{x \to 0}} \frac{{2}}{{x^5}} x→0limx52
发现趋于无穷
根据这三个证明我们发现了什么规律呢?
1:大于分母的阶数,最后和分母约分后,自身趋向于0
2:有小于分母的阶数,那部分极限趋于无穷大。(原因是因为,最小阶数被削的只剩下常数,其余部分不用削了,直接全为0即可)
什么时候能换什么时候不能换?
简单直接,不要用部分泰勒去换,我每次换都换一整个泰勒,这样本身就是等价替换不会出错,那泰勒无限长我该怎么办?
也简单根据我们发现的规律第一条,比分母大的阶数我们就不要了,反正后面都会趋于0
而不是简单的记,加减不能换,乘除才能换
参考视频
等价无穷小原理 什么时候可以换/不能换