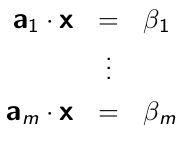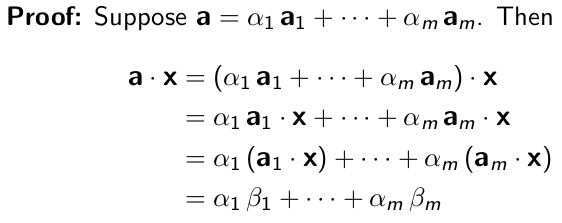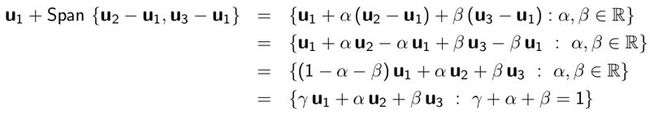Coding the Matrix (2)：向量空间

 

1. 线性组合

概念很简单：

当然，这里向量前面的系数都是标量。

 

2. Span

向量v1，v2，.... ，vn的所有线性组合构成的集合，称为v1，v2，... ，vn的张成（span）。向量v1，v2，...vn的张成记为Span{v1，v2，... ，vn}。

回顾上一次课里面的电脑登陆认证的过程，假设黑客知道使用 GF(2) 加密，截获到一组电脑的问题 alpha 以及用户的回答 beta：

那么即使黑客不知道密码， alpha 所组成的 span 里面的所有问题都可以通过线性组合来得到答案了，证明如下：

 

3. Generator

实际上就是基的概念：

 

4. 向量在实数上的 span

span 就是向量的所有线性组合。一个非零向量的 span 通过原点的线，是一维，两个向量的 span 可能是一维的，亦可能是二维。

一个过原点的平面可以表示成：

{[x, y, z]: [a, b, c] · [x, y, z] = 0}

在几何上， (a, b, c) 又叫法向量。两个平面相交，可以得到一根直线：

可以看到，有两种方法表示一个几何物体：

1. 几个向量的 span
2. 齐次线性方程组（b = 0）的解集。

 

5. Convex Full

向量线性组合系数之和为 1，可以得到 Convex Full, 实际上这就是一个仿射组合。两个二维向量的 Convex Full 是一条线段，三个三维向量的 Convex Full 是一个三角形。

 

6. 仿射空间和仿射组合

过三个点 u1, u2, u3 的平面可以表示成 u1 + span{u2-u1, u3-u1},进一步可以推导如下：

同样的仿射组合的定义可以表示成：

和上面的推导一样，实际上

 

7. 齐次与非齐次线性方程组

齐次线性方程组的解集表示了一个过原点的几何物体，如点，直线，平面等，这个结集也可以看做一个 span。假设 U1 和 U2 是非齐次方程组的解，那么将 U1 和 U2 分别带到方程组，想减可以得到 U1 - U2 是齐次方程的组。所以有：

联系第6小节中的推导，假设 U1， U1, U3 是非齐次线性方程的三个解，那么 U3 -U1 和 U2 -U1 必定是齐次线性方程组的两个解，可以看到，非齐次方程组的解就在  u1 + span{u2-u1, u3-u1} 的仿射空间内。