二分图常见建图方法

 

　　二分图是图论比较重要的一部分，在实际生活中有广泛的应用，比如，分配工作时如何最优分配使得尽可能多的人做自己擅长或感兴趣的时等等出现匹配的问题都需要用二分图解决。不过，二分图的应用不仅仅在这些比较直观上的匹配问题上用到，还有很多实际问题可以通过二分图的一些性质，来匹配解决，比如：如何在一个超市里装最少的摄像头来覆盖整个超市，如何在边防设立最少的岗哨覆盖整个军营等等，在二分图中就叫做最小点覆盖。当然，还有最小边覆盖，最小支配集，最大独立集等都可以应用到实际问题中。

　　上面这些性质固然重要，是我们应用的理论基础。但实际中的许多问题，直观上和二分图都没有什么联系，这就需要我们掌握一些最基础的建图的方法，只有把实际问题转换成二分图后，我们才能很好的利用二分图的性质为我们服务。

 

正文如下：

常见建图模型

法一   行列匹配法

1	0	1
0	1	0
1	0	0

          

上图是一个3 * 3 的矩阵，方格内的1表示这个地方有敌人，0表示没有敌人，现在我们有很多箭，每根箭可以杀死一行或者一列的敌人，问题是，我们要杀死所有的敌人至要用到

几根箭？

初看似乎和最大二分图没有什么相关联的，然而如果我们转换一下视角，这样思考：我们要杀死某个敌人，只要让他所在的位置有箭经过就行。也就是所有的位置都被箭覆盖就行，对就是覆盖，就是顶点的最小覆盖，既然是顶点的最小覆盖，而且我们要杀的是敌人，那么我们的点就应该是敌人的位子，即（行列）对于上面那个图我么可以建立下面这个模型

有人在的坐标是（1,1  1,3   2,2   3,1） 我们就用这几个点的横纵坐标建图

     

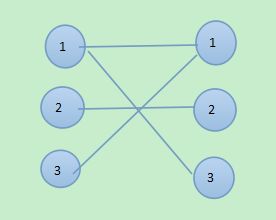
（每个点的横坐标是第一部分，纵坐标是另一部分，被边相连的两个数字表示一个点）

上面我们说过，一个二分图的最小顶点覆盖就是要找到最少的边把所有的顶点覆盖，正好符合这个题的要求，上面还给出了一个性质，即二分图的最小顶点覆盖是等于二分图的最大匹配。所以我们只需要对上面的那个二分图就最大匹配就行，这样把原本的问题转变的很简单了。

 

 

法二  黑白染色法

1	0	1
1	1	1
0	0	1

　　又是一个图，要求是把方格里的所有的1改为零，一次最多只能修改相邻的两个，问最少需要修改几次？ 又是一个求最值得问题，但是似乎用于求最值的算法（贪心，动态规划……）都派不上用场，既然在这里提出，那么他肯定能用二分图最大匹配解决，关键是如何建图？

　　既然是每次只能拿相邻的两个，是两个，正好我们匹配的时候也是找两个进行匹配，这是否就是这个题和最大二分图匹配相联系的地方呢？  对 就是这里。但是每个点能和他四周的四个点匹配，那么我们怎么把所有的点分成来那个部分呢？   对  就是要把第i个点放到第一部分，第i个点周围的四个点放到第二部分，再把这四个点周围的16点放到第1部分

有了这样的思想，我们只需对原图做这样的改动：黑白染色使四周和中间的颜色不同。

 

白1	黑	白5
黑2	白3	黑4
白	黑	白6

图中黑白的意思是就是把点分类，图里的1,2,3,4,5,6表示的就是上面那个0,1图的1的个数

然后建图，把相邻的点相连，比如说1和2   2和3 。。。。。。。

白色       黑色

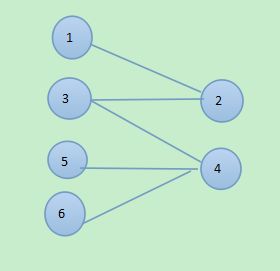
然后要把所有一改为零，也就是要对每个点都操作，每个点都要有，那不就是最小顶点覆盖吗？对，这个问题有解决了。

 

法三  反建法

问题背景：一个极度封建的老师要带同学们出去玩，但是他怕在途中同学之间发生恋情

老师研究了一下发现，满足下面几种条件的两个同学之间发生恋情的可能性很小

1》身高差 > 40             2>性别相同

3》爱好不同的音乐          4>爱好同类型的运动

显然如果我们用满足上面条件的同学之间建边那么最后建立起来的就不是二分图了。稍微观察一下，男生之间我们是随便带的，女生也是，因为他们彼此性别相同。因此我们就可以把男女分为两部分，那么男女之间如何建边？如果我们把男女满足不发生恋情的连起来，那么求出来的最大匹配没有代表性，不能得到我们想要的结果。因此我们用反建法，把男女中可能发生恋情的建立边。也就是说把身高差<=40 或 爱好相同音乐 或 爱好不同类型运动的男女同学之间用边连起来。 然后求一个最大独立集，最大独立集的原则不就是找到一个点集，使得集合内的点互不相连且点尽量多吗？我们把可能发生恋情的男女相连，那么最大独立集不就是我们要找的不可能发生恋情的人的集合吗？ 那么， 这个问题解决了！

 

 

法四  拆点法

 

拆点法是用于解决最小路径覆盖问题的，给出一个图

 

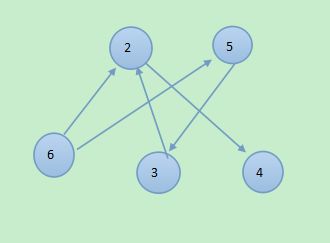
要找到几条路径，可以把所有的点经过，并且路径之间不可以交叉。我们的做法是把点拆成两部分（点1 拆为x1,y1. 点2拆为x2,y2……）

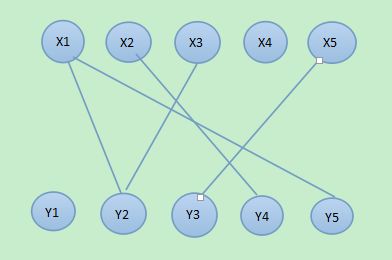
如果我们对这个图求二分图的最大匹配，你会发现每个匹配对应着一个路径覆盖，因此，此二分图的最大匹配即：原图中的最小路径覆盖上的边的个数（路径是由0条，1条或多条边组成的）。那么原图的最小路径覆盖数 = 原图顶点数 – 最小路径上的边数  也就是 原图的最小路径覆盖数 =  原图顶点数 – 二分图最大匹配数。

 

法五  一行变多行，一列变多列

 

		###
###
		###	###
	###

 

　　上面是一个4*4的方格，方格内的###表示墙，我们要在表格内没有墙的地方建立碉堡，而且要保证任何两个碉堡之间互相不能攻击，问最多能建多少个碉堡？是否感觉像第一个题呢？如果我们向第一个题那样建图，那么最后求出来的最大匹配也就是行和列的匹配。而且这个匹配满足了所有匹配都是不同行不同列（匹配本身的性质就是每个点至多属于匹配中的某个边）。但是这样的建图的话，我们墙怎么处理？  有墙的地方就相当于把这一行和这一列分成了两行，两列。

 

例

###

 

   等价于   

 

  还是一行 

###

 

  等价于 

###

###

和 

###

###

 

一行变成了两行，对，就是这么分的。

1,1	1,2	###	1,4
###	2,2	2,3	2,4
3,1	3,2	###	###
4,1	###	4,3	4,4

 

原图 

1,1	1,2	###	2,4
###	3,2	3,3	3,4
4,5	4,2	###	###
5,5	###	6,6	6,7

 

（因为有了墙所以第一行变为两行） 

（因为上面有了二行固只能从第三行开始）

（因为第一列有了墙，固列数增加为5）

（第3,4列有了墙，固列数增加到了6和7）。

 一行变多行，一列变多列后我们按照这个编号建图即可：

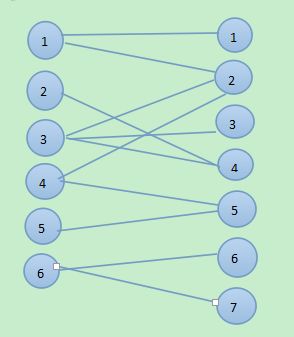
对这个图求二分图最大匹配即可。这个问题也解决了！

一个应用于求二分图匹配的算法—匈牙利算法，巧妙的应用找增广轨的方式，使得求二分图最大匹配即变得高效，而且也变得容易理解，

　　这就有了艺术的感觉，然而，一个应用于二分图的操作，却可以把其他看似和二分图没关系的事情，通过巧妙的，艺术性的手笔转化为二分图问题，这是多么的美妙。算法是很神奇的东西，总是让人摸不着头脑，当你认为自己对某种算法很熟悉的时候，你总会立即发现其实你只是对他有了一点点认识，这就是算法。

 

本主体资料来源网络，由本人整理。