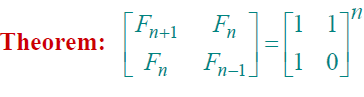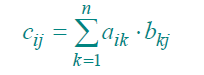算法打基础——分治法

第三讲主要是讲divide-and-conquer, 与上一讲结合的很紧密，因为分治法几乎都是递归啦，求复杂度必备啊！

 这一讲的主要知识点有：

1.分治法主要步骤 （后面就全是分治法的应用了）2.二分搜索 3.快速求幂 4.快速求斐波那契数列  5.矩阵连乘(Strassen's algorithm)   下面分别来介绍

分治法的主要步骤： 分为三步。

1. 将问题分解成子问题

2.递归的去解决这些子问题

3. 合并这些子问题

举前面的归并排序来说，这是非常典型的分治法。

1.Divide:Trivial.

2.Conquer:Recursively sort 2subarrays.

3.Combine:Linear-time merge

复杂度：T(n)=2T(n/2)+Θ(n) 分析：2-子问题个数 n/2-子问题规模 Θ(n)-合并以及其他处理

二分搜索：

Find an element in a sorted array:

1.Divide:Check middle element.

2.Conquer:Recursively search 1subarray.

3.Combine:Trivial.

 

对二分查找的分析：T(n) = T(n/2)+Θ(1): 由主定理 case2 可以得到复杂度T(n)=Θ(logn)

快速求幂：Compute aⁿ, where n ∈N.

一般解法当然就是做n次乘法，复杂度是Θ(n). 

用分治法来处理，将其分成n/2的规模来递归解决，其方案是：

an=a^n/2 ⋅a^n/2                     if n is even;

      a^(n–1)/2 ⋅a^(n–1)/2 ⋅a   if n is odd.

分成这两种情况来解决，注意 因为乘法的两边都是相同的数，所以只用计算一次，故他的复杂度是： T(n)=T(n/2)+Θ(1) 即 T(n)=Θ(logn)

快速求斐波那契数列：这个数列是非常重要的数列，给出他的定义

 

 如果按照这个递归式去解这个问题，复杂度将是：Ω(Kⁿ) (即指数时间)，其中K=(1+sqr(5))/2;这是非常高的一个复杂度。

还可以按照自底向上的步骤：按顺序计算F0,F1,F2,...Fn。由于之前那个递归式需要处理大量重复的子式，而现在不用了，其复杂度是Θ(n）。

或者用一个一般式来求，即F_n=K_n/sqr(5) 且四舍五入到最近整数。这种算法的就是计算一个数的n次方，最快也可以达到Θ(log n）。但是这个方法不可靠！因为计算机的浮点运算可能会导致错误的四舍五入结果！

然后这里引入了一个非常神奇的定理：

用这个定理去求斐波那契数列的第n项就不用涉及到浮点运算了，而且这是n个2*2矩阵乘法，其复杂度同数的n次幂，所以复杂度是Θ(log n)

这个定理的证明可以使用数学归纳法，很容易证明。

矩阵乘法（strassen's 公式）

 一般的，求矩阵乘法的运算是：

使用伪代码表示为： 

for i=1 to n

   do for j=1 to n

      do c_ij = 0

          for k=1 to n

              do c_ij = c_ij + a_ik * b_kj

 由此也可以得到复杂度是 Θ(n³)

我们想使用分治法的思想去解决矩阵乘法问题，所以首先将n*n的矩阵分开，分成4块。

根据矩阵运算规则，我们也知道我们将n*n矩阵运算，分解成了8个(n/2)*(n/2)的乘法，以及4个两个同样的小矩阵的加法(矩阵加法的复杂度是那n²)

可以得到新的复杂度是： T(n) = 8T(n/2) + Θ(n²)

这个递推式可以根据主定理的case 1，得出复杂度仍然是 Θ(n³)

由此我们给出Strassen's idea: 其主要思想是加法的复杂度是n2,乘法的复杂度是n3,所以尽量减少乘法，增加加法的个数。最后搞了一个7个乘法的表达式。

T(n) = 7T(n/2) + Θ(n2)。  T(n) = Θ(nlg7) 降低了复杂度

 最后附上这章的自己写的算法代码：

 1 /////////////////////////CLRS   video lec3  二分搜索/////////////////////////////////////////////////
 2 //二分搜索是针对已排序序列的哦！O(lg n)的复杂度  /////////////////////////////////////////////////////
 3 
 4 
 5 #include<iostream>
 6 using namespace std;
 7 
 8 int main()
 9 {
10     int arr[10] ={1,4,5,7,9,10,15,19,29,35};
11     int find,flag=1,middle;
12     cin>>find;
13     int a=0,b=9;               // a,b 是左右的边界，在这个范围内搜索
14     while(a<b)                 //这个判结束的条件很重要！！
15     {
16         middle = (a+b)/2;
17         if(arr[middle]>find)
18             b=middle-1;
19         else if(arr[middle]<find)
20             a=middle+1;
21         else{
22             cout<<middle<<endl;
23             break;
24         }
25     }
26     return 0;
27 }

Binarysearch

 1 /////////////////////////CLRS   video lec3  快速求幂/////////////////////////////////////////////////
 2 //O(lg n)的复杂度  /////////////////////////////////////////////////////
 3 
 4 
 5 #include<iostream>
 6 using namespace std;
 7 
 8 long mypower(int a,int n)
 9 {
10     if(n==1) return a;
11     else{
12         long result;
13         if(n%2==0){
14             result = mypower(a,n/2);
15             return result*result;
16         }
17         if(n%2==1){
18             result = mypower(a,(n-1)/2);
19             return result*result*a;
20         }
21     }
22 }
23 
24 int main()
25 {
26     int a=6,n;
27     cin>>n;
28     long result = mypower(a,n);
29     cout<<result<<endl;
30 }

快速求幂