改造的二分法无限分类
那么理想中的树型结构应具备哪些特点呢?数据存储冗余小、直观性强;方便返回整个树型结构数据;可以很轻松的返回某一子树(方便分层加载);快整获以某节点的祖谱路径;插入、删除、移动节点效率高等等。带着这些需求我查找了很多资料,发现了一种理想的树型结构数据存储及操作算法,改进的前序遍历树模型(The Nested Set Model)。
原理:
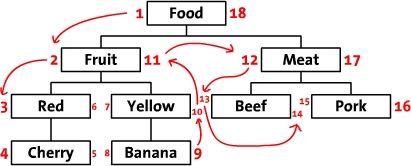
我们先把树按照水平方式摆开。从根节点开始(“Food”),然后他的左边写上1。然后按照树的顺序(从上到下)给“Fruit”的左边写上2。这样,你沿着树的边界走啊走(这就是“遍历”),然后同时在每个节点的左边和右边写上数字。最后,我们回到了根节点“Food”在右边写上18。下面是标上了数字的树,同时把遍历的顺序用箭头标出来了。
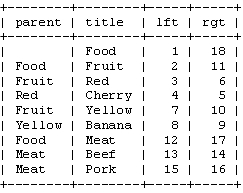
我们称这些数字为左值和右值(如,“Food”的左值是1,右值是18)。正如你所见,这些数字按时了每个节点之间的关系。因为“Red”有3和6两个值,所以,它是有拥有1-18值的“Food”节点的后续。同样的,我们可以推断所有左值大于2并且右值小于11的节点,都是有2-11的“Fruit” 节点的后续。这样,树的结构就通过左值和右值储存下来了。这种数遍整棵树算节点的方法叫做“改进前序遍历树”算法。
表结构设计:
那么我们怎样才能通过一个SQL语句把所有的分类都查询出来呢,而且要求如果是子类的话前面要打几个空格以表现是子分类。要想查询出所有分类很好办:SELECT * FROM category WHERE lft>1 AND lft<18 ORDER BY lft这样的话所有的分类都出来了,但是谁是谁的子类却分不清,那么怎么办呢?我们仔细看图不难发现如果相邻的两条记录的右值第一条的右值比第二条的大那么就是他的父类,比如food的右值是18而fruit的右值是11 那么food是fruit的父类,但是又要考虑到多级目录。于是有了这样的设计,我们用一个数组来存储上一条记录的右值,再把它和本条记录的右值比较,如果前者比后者小,说明不是父子关系,就用array_pop弹出数组,否则就保留,之后根据数组的大小来打印空格。这样就解决了这个问题。代码如下
表结构:
--
-- 表的结构 `category`
--
CREATE TABLE IF NOT EXISTS `category` (
`id` int(11) NOT NULL AUTO_INCREMENT,
`type` int(11) NOT NULL COMMENT '1为文章类型2为产品类型3为下载类型',
`title` varchar(50) NOT NULL,
`lft` int(11) NOT NULL,
`rgt` int(11) NOT NULL,
`lorder` int(11) NOT NULL COMMENT '排序',
`create_time` int(11) NOT NULL,
PRIMARY KEY (`id`)
) ENGINE=InnoDB DEFAULT CHARSET=utf8 AUTO_INCREMENT=10 ;
--
-- 导出表中的数据 `category`
--
INSERT INTO `category` (`id`, `type`, `title`, `lft`, `rgt`, `lorder`, `create_time`) VALUES
(1, 1, '顶级栏目', 1, 18, 1, 1261964806),
(2, 1, '公司简介', 14, 17, 50, 1264586212),
(3, 1, '新闻', 12, 13, 50, 1264586226),
(4, 2, '公司产品', 10, 11, 50, 1264586249),
(5, 1, '荣誉资质', 8, 9, 50, 1264586270),
(6, 3, '资料下载', 6, 7, 50, 1264586295),
(7, 1, '人才招聘', 4, 5, 50, 1264586314),
(8, 1, '留言板', 2, 3, 50, 1264586884),
(9, 1, '总裁', 15, 16, 50, 1267771951);
/**
* 显示树,把所有的节点都显示出来。
* 1、先得到根结点的左右值(默认根节点的title为“顶级目录”)。
* 2、查询左右值在根节点的左右值范围内的记录,并且根据左值排序。
* 3、如果本次记录右值大于前次记录的右值则为子分类,输出时候加空格。
* @return array
**/
function display_tree(){
//获得root左边和右边的值
$arr_lr = $this->category->where("title = '顶级栏目'")->find();
//print_r($arr_lr);
if($arr_lr){
$right = array();
$arr_tree = $this->category->query("SELECT id, type, title, rgt FROM category WHERE lft >= ". $arr_lr['lft'] ." AND lft <=".$arr_lr['rgt']." ORDER BY lft");
foreach($arr_tree as $v){
if(count($right)){
while ($right[count($right) -1] < $v['rgt']){
array_pop($right);
}
}
$title = $v['title'];
if(count($right)){
$title = '|-'.$title;
}
$arr_list[] = array('id' => $v['id'], 'type' => $type, 'title' => str_repeat(' ', count($right)).$title, 'name' =>$v['title']);
$right[] = $v['rgt'];
}
return $arr_list;
}
}
好了 只要这样所有的分类都可以一次性查询出来了,而不用通过递归了。
下面的问题是怎样进行插入、删除和修改操作
插入:插入操作很简单找到其父节点,之后把左值和右值大于父节点左值的节点的左右值加上2,之后再插入本节点,左右值分别为父节点左值加一和加二,可以用一个存储过程来操作:
CREATE PROCEDURE `category_insert_by_parent`(IN pid INT,IN title VARCHAR(20), IN type INT, IN l_order INT, IN pubtime INT)
BEGIN
DECLARE myLeft INT;
SELECT lft into myLeft FROM category WHERE id= pid;
UPDATE qy_category SET rgt = rgt + 2 WHERE rgt > myLeft;
UPDATE qy_category SET lft = lft + 2 WHERE lft > myLeft;
INSERT INTO qy_category(type, title, lft, rgt, lorder, create_time) VALUES(type ,title, myLeft + 1, myLeft + 2, l_order, pubtime);
commit;
END
删除操作:
删除的原理:1.得到要删除节点的左右值,并得到他们的差再加一,@mywidth = @rgt - @lft + 1;
2.删除左右值在本节点之间的节点
3.修改条件为大于本节点右值的所有节点,操作为把他们的左右值都减去@mywidth
存储过程如下:
CREATE PROCEDURE `category_delete_by_key`(IN id INT)
BEGIN
SELECT @myLeft := lft, @myRight := rgt, @myWidth := rgt - lft + 1
FROM category
WHERE id = id;
DELETE FROM category WHERE lft BETWEEN @myLeft AND @myRight;
UPDATE nested_category SET rgt = rgt - @myWidth WHERE rgt > @myRight;
UPDATE nested_category SET lft = lft - @myWidth WHERE lft > @myRight;
修改:
要命的修改操作,本人看了很久也没有看出什么规律出来,只要出此下策,先删除再插入,只要调用上面2个存储过程就可以了!
总结:查询方便,但是增删改操作有点繁琐,但是一般分类此类操作不是很多,还是查询用的多,再说弄个存储过程也方便!无限分类的方法还有,下回再介绍第二种!