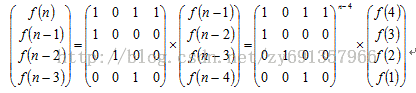【递推+矩阵快速幂】【HDU2604】【Queuing】

Queuing

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3032    Accepted Submission(s): 1379

Problem Description

Queues and Priority Queues are data structures which are known to most computer scientists. The Queue occurs often in our daily life. There are many people lined up at the lunch time. 

  Now we define that ‘f’ is short for female and ‘m’ is short for male. If the queue’s length is L, then there are 2 ^L numbers of queues. For example, if L = 2, then they are ff, mm, fm, mf . If there exists a subqueue as fmf or fff, we call it O-queue else it is a E-queue.
Your task is to calculate the number of E-queues mod M with length L by writing a program.

 

Input

Input a length L (0 <= L <= 10  ⁶) and M.

 

Output

Output K mod M(1 <= M <= 30) where K is the number of E-queues with length L.

 

Sample Input

   
   
   
   

    
    
    
    3 8
4 7
4 8
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    6
2
1
   
   
   
   

 

Author

WhereIsHeroFrom

 

FFF FMF

一.找递推公式

考虑最后若直接加M 显然可以成立 所以F[n]=F[n-1]+X

若要在后面加F 考虑N-1是没办法的

考虑N-2 FF MF 依旧没办法

考虑N-3 FFF FMF MMF MFF （FFF,FMF 已经不可能 不考虑）

显然添加MMF 前面N-3无论是什么都不可能会出现FFF,FMF了

所以F[n]=F[n-1]+F[n-3]+X

但是 若添加MFF 可能会出现FMFF

考虑N-4 FMFF MMFF 显然MMFF可以取了

所以 F[n]=F[n-1]+F[n-3]+F[n-4]

二.设计矩阵

注：矩阵十分好设计  第一排即为递推公式的系数

      以后几排类似于单位矩阵

三.矩阵快速幂

类似非递归快速幂

node kuaisumi(node A,int N,int mod)
{
	node di=e;
	while(N>0)
	{
		if(N&1)
		{
			di=MatrixMult(di,A,mod);
		}
		A=MatrixMult(A,A,mod);
		N=N>>1;
	}
	return di;
}

最后代码如下：

#include <cstdio>  
#include <cstdlib>  
#include <cmath>  
#include <cstring>  
#include <ctime>  
#include <algorithm>  
#include <iostream>
#include <sstream>
#include <string>
#define oo 0x13131313   
using namespace std;
int L,M;
struct node
{
	int mat[5][5];
}a,e,ans;
int mat2[5];
void CSH()
{
	mat2[1]=9;
	mat2[2]=6;
	mat2[3]=4;
	mat2[4]=2;
	for(int i=1;i<=4;i++)
{
		e.mat[i][i]=1;
		mat2[i]=mat2[i]%M;
}
	memset(a.mat,0,sizeof(a.mat));
	a.mat[1][1]=a.mat[1][3]=a.mat[1][4]=1;
	a.mat[2][1]=a.mat[3][2]=a.mat[4][3]=1;
}
node MatrixMult(node A,node B,int mod)
{
	node p;
	memset(p.mat,0,sizeof(p.mat));
	for(int i=1;i<=4;i++)
	 for(int j=1;j<=4;j++)
	 {
	 	 for(int k=1;k<=4;k++)
	 	p.mat[i][j]+=A.mat[i][k]*B.mat[k][j];
	 	p.mat[i][j]=p.mat[i][j]%mod;
	 }
	 return p;
}
node kuaisumi(node A,int N,int mod)
{
	node di=e;
	while(N>0)
	{
		if(N&1)
		{
			di=MatrixMult(di,A,mod);
		}
		A=MatrixMult(A,A,mod);
		N=N>>1;
	}
	return di;
}
void solve()
{
	int ANS=0;
	for(int i=1;i<=4;i++)
	{
		ANS+=ans.mat[1][i]*mat2[i];
		ANS=ANS%M;
	}
	printf("%d\n",ANS);
}
int main()
{
	while(cin>>L>>M)
	{
		CSH();
		if(L>4)
		ans=kuaisumi(a,L-4,M);
		if(L>4)
		solve();
		else 
		printf("%d\n",mat2[L]);
	}
	return 0;
}