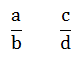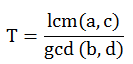HDU 1713 相遇周期(数学 最大公约数与最小公倍数)

相遇周期

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

Problem Description

2007年3月26日，在中俄两国元首的见证下，中国国家航天局局长孙来燕与俄罗斯联邦航天局局长别尔米诺夫共同签署了《中国国家航天局和俄罗斯联邦航天局关于联合探测火星-火卫一合作的协议》，确定中俄双方将于2009年联合对火星及其卫星“火卫一”进行探测。

而卫星是进行这些探测的重要工具，我们的问题是已知两颗卫星的运行周期，求它们的相遇周期。

 

Input

输入数据的第一行为一个正整数T, 表示测试数据的组数. 然后是T组测试数据. 每组测试数据包含两组正整数，用空格隔开。每组包含两个正整数，表示转n圈需要的天数(26501/6335，表示转26501圈要6335天)，用'/'隔开。

 

Output

对于每组测试数据, 输出它们的相遇周期，如果相遇周期是整数则用整数表示，否则用最简分数表示。

 

Sample Input

   
   
   
   

    
    
    
    2
26501/6335 18468/42
29359/11479 15725/19170
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    81570078/7
5431415
   
   
   
   

 

/************************************************************************/

说实话，刚拿到这题的时候，我还在纠结于题目所给的样例，我怎么也凑不出输入与输出二者的关系，按理来说，要算相遇周期，应该是经过相同时间之后，两颗卫星差整数圈，可能是我脑子短路，一开始，我愣是拿26501/6335和81570078/7相乘，可是结果偏偏不是整数，后来，偶然将26501/6335倒一下，即6335/26501，这样再和81570078/7相乘就是整数了，原来一直是我乘反了

现在想想也是，本就该这么算，先算出跑一圈所需要的天数，这样为了将圈数凑整，就要乘以二者的最小公倍数

于是，我们可以得到这样一个公式，对于初始给定的

相遇周期为

具体看代码，有不理解的再提出

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<stdlib.h>
#include<cmath>
#include<string>
#include<algorithm>
#include<iostream>
#define exp 1e-10
using namespace std;
const int N = 1000000;
const int inf = 1000000000;
const int mod = 258280327;
__int64 gcd(__int64 x,__int64 y)
{
    while(x!=y)
        if(x>y)
            x-=y;
        else
            y-=x;
    return x;
}
__int64 lcm(__int64 x,__int64 y)
{
    return x*y/gcd(x,y);
}
int main()
{
    int t;
    __int64 a,b,c,d,x,y;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%I64d/%I64d%I64d/%I64d",&a,&b,&c,&d);
        x=gcd(a,b);
        a/=x;b/=x;
        x=gcd(c,d);
        c/=x;d/=x;
        x=lcm(a,c);
        y=gcd(b,d);
        if(x%y)
            printf("%I64d/%I64d\n",x,y);
        else
            printf("%I64d\n",x/y);
    }
    return 0;
}

菜鸟成长记