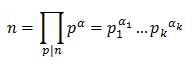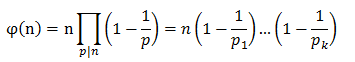RSA公钥密码体制
中国剩余定理
《孙子算经》中有记载:“今有物不知其数,三三数之余二,五五数之余三,七七数之余二,问物几何?”意思是,有一些物品,如果3个3个地数,最后剩余2个;如果5个5个地数,最后剩余3个;如果7个7个地数,最后剩余2个;求这些物品一共多少个?
这就是中国剩余定理,或称孙子定理。明代数学家程大位把这个问题的算法编程四句歌诀:“三人同行七十稀,五树梅花廿一枝;七子团员正半月,除百零五便得知。”意思是,一个数用3除,所得余数乘以70;用5除,所得余数乘以21;用7除,所得余数乘以15;最后把这些乘积加起来再减去105的倍数,就知道这个数了。
《孙子算经》中这个问题的解法是:70x2+21x3+15x2=233, 233-105x2=23。我们做如下思考:
70是5和7的公倍数,且被3除余1;
21是3和7的公倍数,且被5除余1;
15是3和5的公倍数,且被7除余1。
这样任意一个系数乘以对应余数所得的积,被对应除数除后所得的余数恰好等于对应余数,且该积仍然能被其他两个除数整除。因此,三个积相加并不互相影响各自被对应除数除后所得的余数。
即70a+21b+15c是被3除余a,被5除余b,被7除余c的数。
欧拉函数
设m是一个正整数,则m个整数0,1,2,...,m-1中与m互质的整数的个数,记作φ(m)。例如:m=10,与10互质的整数为1,3,7,9,所以φ(m)=4,称为欧拉(Euler)函数。
第1种情况:φ(1)=1;
第2种情况:当n是质数时,φ(n)=n-1;
第3种情况:当时,,其中p为质数,证明:只有当一个数不是p的倍数时,才能与n互质,p的倍数有1xp, 2xp, 3xp, p^(k-1)xp,共p^(k-1)个;
第4种情况:当![]() 时,,其中p1和p2是互质的两个数,证明具体请参考《信息安全数学基础 陈恭亮 编著》;
时,,其中p1和p2是互质的两个数,证明具体请参考《信息安全数学基础 陈恭亮 编著》;
欧拉定理
欧拉定理(Euler)设整数m>1,整数a满足(a, m)=1,则aφ(m) ≡ 1(mod m),欧拉定理证明略。证明比较复杂,需要先看懂《信息安全数学基础》前两章的很多定理。
费马小定理(Fermat)设p是一个质数,则对任意整数a,有ap ≡ a(mod p),证明:
(a)若a被p整除,则同时有 a ≡ 0(mod p),与ap ≡ 0(mod p),因此ap ≡ a(mod p).
(b)若a不被p整除,则(a, p)=1,注意φ(p) = p-1,根据欧拉定理有ap-1 ≡ a(mod p),则进一步可得
p|ap-1 - 1,所以p|ap - a,即ap ≡ a(mod p)。
模m可逆元 如果存在整数a,m使得(a, m)=1,那么一定可以找到整数a',使得aa' ≡ 1(mod m),则a叫做模m可逆元,这时a'叫做a的模m可逆元,记作a' ≡ a-1 (mod m)。欧拉定理就是拿来证明模m可逆元的存在的,推导如下:aφ(m) = a x aφ(m)-1 ≡ 1(mod m). 可以得出aφ(m)-1就是a的模m可逆元。
RSA算法
下面我们先介绍RSA算法,
(1)随机选择两个素数,p=17,q=11;
(2)计算n=pq=17x11=187;
(3)计算φ(n)=φ(pq)=φ(p)φ(q)=(p-1)(q-1)=16x10=160,欧拉函数第2、4种情况;
(4)选择e使得(e, φ(n))=1且小于φ(n),这里选择e=7;
(5)确定d使得de≡1 mod φ(n)且d<φ(n),根据模m可逆元可知,d一定存在;
(6)公钥Kpublic={e, n},私钥Kprivate={d, n},加密算法Y=Xe mod n,解密算法X=Yd mod n,接下来证明解密结果一定等于原文,我们仅需证明X=Yd mod n=(Xe)d mod n=Xed mod n,
我们可知ed=k·φ(n)+1,现分2种情况:
①X与n互质,即(X, n)=1时,根据欧拉定理有Xφ(n) ≡ 1(mod n),根据取模运算性质(a·b)%p = (a%p · b%p)%p可知Xk·φ(n) % n = 1,即Xk·φ(n) ≡ 1(mod n),再有Xk·φ(n)+1 ≡ X(mod n),即Xed ≡ X(mod n),成立.
②X与n不互质,即(X, n)=p或(X, n)=q,不妨设X=ap,又由于X<n(n值一般取很大,后面解释),所以X不可能被q整除,否则就变成X=a'pq>=n,即(X=ap, q)=1,根据欧拉定理有Xφ(q)≡1(mod q),进一步可推出
Xkφ(p)φ(q)≡1(mod q),即Xkφ(pq)≡Xkφ(n)≡1(mod q),改写成Xkφ(n)=1+bq,两边同乘以X,得到
Xkφ(n)+1=X+bqX,则Xed=X+bqap=X+k'pq=X+k'n,Xed ≡ X(mod n),成立.
证毕。
RSA可靠性
在RSA算法中,出现p, q, n, φ(n), e, d,其中公钥<e, n>,私钥<d, n>,我们想要从公钥获得d,需要知道φ(n),而φ(n)的计算需要p跟q,当n极大时穷举得到φ(n)不太可行,分解n得到p跟q也不太可行(大整数的因数分解一直是一个数学难题,例如无法一眼看出3233=61×53,只能穷举),所以RSA算法是可靠的。这里n极大,也就自然造成了X<n。
RSA例子
假设输入明文M=88,加密时,887 mod 187 = 11,密文为11;解密时,1123 mod 187 = 88,得到明文88.
Reference
什么是中国剩余定理
RSA算法原理(一)
RSA算法原理(二)
《密码编码学与网络安全——原理与实践(第五版)》 [美] William Stallings 著
《信息安全数学基础》 陈恭亮 著