python 机器学习——从感知机算法到各种最优化方法的应用（python）

感知机算法的基本形式及一些基于最优化方法的感知机算法的变体具有机器学习的典型处理框架，且理论较为简单，实现并不复杂。同时作为单层神经网络的感知机，也是支持向量机和神经网络的基础。

本文的主要内容包括：

• 为什么说通过感知机算法的推导和实践便迈进了机器学习的大门？
• 感知机算法的学习策略是怎样的？
• 不同感知机算法之间的真正区别是什么？
• 关于感知机算法都有哪些损失函数和权重更新的形式？
• 为什么需要对数据进行标准化或者叫特征缩放？
• 如何对数据进行标准化？
• 如何利用python实现感知机算法及其不同的变体？
• 如何利用python（matplotlib）实现对数据的可视化工作？

一、 准备

本文算法的任务是通过应用感知机算法及其不同最优化方法下（GD：梯度下降，SGD：随机梯度下降）的版本实现对一个线性可分的二维（也可应用到多维，无非是np.dot(x, w[1:]), x和w维度的不同，对算法的实现没有任何影响，只是出于可视化的需要）二类别样本的分类，这中间涉及一些简单的数据处理（比如standardized，标准化，或者叫特征缩放，feature scaling，又比如数据shuffle），以及更为重要的通过matplotlib实现数据可视化，来一窥机器学习算法的全貌。

1.1 数据集

本文待分类的数据集(iris.data)是一种CSV（逗号分隔符，Comma-Separated Value）文件。
点击这里可查看对数据集的介绍，这里对其中的属性介绍如下：

1. sepal length in cm
2. sepal width in cm
3. petal length in cm
4. petal width in cm
5. class:
   – Iris Setosa
   – Iris Versicolour
   – Iris Virginica

为了说明问题的方便，本文只涉及二分类问题，考虑前100个样本，即Iris-setosa和Iris-versicolor类的样本各占一半，为了低维数据可视化的需要，考虑第一和第三个属性，即sepal length和petal length。

import matplotlib.pyplot as plt
plt.scatter(X[y==1, 0], X[y==1, 1], color='red', 
                marker='o', label='setosa')
plt.scatter(X[y==-1, 0], X[y==-1, 1], color='blue', 
                marker='x', label='versicolor')

这100个样本的散列图如下：

注：iris，鸢尾花。鸢尾花张啥样（这才是真正的可视化呀）？

1.2 基本工具

1.2.1 pandas——read in data

import pandas as pd

• pandas文件读取函数

df = pd.read_csv('https://archive.ics.uci.edu/ml/'
                'machine-learning-databases/iris/iris.data', header=None)   
                                    # 返回一种DataFrame结构文件
print(df.tail())                    # 验证是否读取正确

• DataFrame，pandas中的一种数据结构

通过pd.read_csv()读取到待处理的数据集并保存到DataFrame后，便可通过DataFrame强大的切片和索引能力，生成机器学习算法所需要的数据格式。

# 只考虑第一和第三个属性值，为了可视化的的需要
# 此时X的类型是numpy.ndarray
X = df.iloc[[0:100, [0, 2]].values()    
y = df.iloc[[0:100], 4].values # 将string类型的类别标签转化为二分类标签 y = np.where(y == 'Iris-seosta', -1, 1)

1.2.2 numpy——process data

1.2.3 matplotlib——visualize data

二、 基本概念与定义

感知机是二分类的线性模型，以实例的特征向量（不同于线性代数的特征向量，其实线代里的特征向量更准确的叫法应该是本征向量）作为输入，以 ±1 类别标签作为输出。

输入空间（input space 或者叫 feature space） X⊆Rn ，输出空间（output space） Y=+1,−1 。
我们定义激励函数（activation function， ϕ(z) ），它以输入x与权重w的内积作为输入， z=wTx=w0x0+w1x1+w2x2+…+wdxd ，也就是所谓的net_input（或者叫score），以最终的预测类别作为输出.

感知机算法中， ϕ(⋅) 是一个简单的单位阶跃函数（有时也称作heaviside step function）：

ϕ(z)={+1,−1,z≥0otherwise

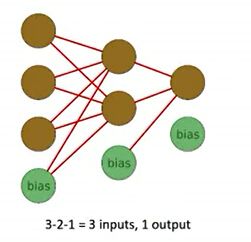
注：关于bias的两种解释，解释1： w1x1+w2x2+…+wdxd+w0∗1 ，如下图（三层神经网络）示，这里的偏置用来表征与输入无关的一些系统自身的因素，更具数学意味的说法是将数据的输入空间提升了一维。

解释之二，在激励函数（activation function）中，对输进行了加权求和之后的net_input(或者叫score)，如果大于指定的阈值 θ ，则输出为1，否则为-1

z=w1x1+w2x2+…+wdxdϕ(z)={+1,−1,z≥θotherwise

转化为如下的形式：

z=w0x0+w1x1+w2x2+…+wdxd=wTxϕ(z)={+1,−1,z≥0otherwise

其中 w0=−θ ， x0=1 。

殊途同归，两中不同的解释得到相同的形式。

三、 感知机学习算法的原始形式（以误分数为损失函数）

以误分数作为损失函数的形式如下：

J=∑i=1N1y(i)≠ϕ(wTx(i))

其权重更新方式如下：

w:=w+ΔwΔ=η(y(i)−y^(i))x(i)

其中， η 表示学习率，是一个介于0-1之间的常量，控制更新的步长，在classifier构造时定义。

以二维数据集为例：

Δw0=Δw1=Δw2=η(y(i)−y^(i))η(y(i)−y^(i))x(i)1η(y(i)−y^(i))x(i)2

注意，这里的 Δwj 是按照向量化的做法同步得到的，也即：

self.w_[0] += self.eta * (y - self.predict(x))
self.w_[1:] += self.eta * (y-self.predict(x)) * x
# 这里的self.w_[1:]以及x表示的均是向量

在我们进入python实战之前不妨，先对这一权值更新方式的合理性做一个直观的解释，为什么这样的权值更新是可行的。
监督学习的过程中，真实值和估计值之间差值( y(i)−y^(i) )一共四种情况，
Δw=η(1−1)x(i)=0
Δw=η(−1−−1)x(i)=0
Δw=η(1−−1)x(i)=η(2)x(i)
Δw=η(−1−1)x(i)=η(−2)x(i)

在误分的情况下，所进行的权值更新，以 Δw=η(1−−1)x(i)=η(2)x(i) 为例（将正的估计成了负的），根据上述的权值更新公式得到的更新的方向（+2），恰代表真实值所在的方向。

四、 基于最优化方法的变体（梯度下降、随机梯度下降）

这一节，我们将介绍单层神经网络的另一种实现方法：自适应线性神经元（ADAptive LInear NEuron，AdaLine）。
AdaLine与Rosenblatt’s 基本感知机的关键不同在于，两个具有不同的损失函数及相关的权值更新公式。后者是基于单位阶跃函数( y(i)−y^(i) )，而前者是基于线性激励函数（ yi−ϕ(wTx) ）。在AdaLine中，线性激励函数 ϕ(wTx) 是简单的证同函数，即 ϕ(wTx)=wTx 。

监督学习算法的一大关键在于目标函数（objective function）的定义与设计，目标函数是学习或者训练的过程（learning process）中进行优化的对象。目标函数常常是我们需要最小化的损失函数。在AdaLine算法中，我们可以通过将损失函数 J 定义为平方误差和（sum-squared-error，SSE）的方式来进行对权值的更新，

J==12∑i=1N(y(i)−ϕ(z(i)))212∥y−Xw∥2

12 是为了求导的方便。与单位阶跃函数相比，这种线性激励函数的最大优势在于，损失函数变成了可导的，而且是凸函数，因此我们可以利用梯度下降法找到权值更新的方向来最小化损失函数，即：

w:=Δw=w+Δw−ηΔJ(w)

因为是找使损失函数最小的方向，故权值更新的方向是负梯度方向（ −ηΔJ(w) ）
由损失函数的矩阵形式，我们很容易求出它的梯度：

∂J∂w=−XT(y−Xw)

所以新的权值更新方式：

w=w+ηXT(y−Xw)

五、 python实战

5.1 类接口设计

根据机器学习清晰的两相处理流程（学习或者叫训练，以及预测），再加之面向对象的思想，可对分类器设计如下的接口。

• fit(X, y)

接受样本集X，及样本类别标签y，返回分类器实例

• net_input(X)

接受样本集X，返回样本集与权重的内积 X⋅w （X列代表属性feature，行代表一个观察值observation，w是列向量），但这里要考虑bias的作用，也就是如果X和w都不是增广的话， X⋅w[1:]+w[0] 。

• activation(X)

如：

ϕ(z)={+1,−1,z≥θotherwise

• predict(X)

接受样本集X，返回预测的类别标签 ±1 。如果判别函数是 y=sign(wtx) ，则其python实现形式如下：

return np.where(self.net_predict(X) >= 0., 1, -1)

5.2 感知机的基本形式——以误分数为损失函数

class Perceptron(object):
    def __init__(self, eta=0.01, n_iter=10):
        self.eta = eta
        self.n_iter = n_iter

    def fit(self, X, y):
        self.w_ = np.zeros(1 + X.shape[1])
        self.J_ = []        # 记录每次迭代的误分数
        for _ in range(self.n_iter):
            J = 0
            for xi, yi in zip(X, y):
                delta = yi - self.activation(xi)                
                self.w_[0] += self.eta * delta
                self.w_[1:] += self.eta * delta * xi
                J += int(delta != 0.)
            self.J_.append(J)
        return self
    def net_input(self, X):
        return X.dot(self.w_[1:]) + self.w_[0]
    def activation(self, X):
        # python中的三目运算符
        return np.where(self.net_input(X) >= 0.0, 1, -1)    
    def predict(self, X):
        return np.where(self.net_input(X) >= 0.0, 1, -1)

客户端程序，并显示随着迭代的进行，误分数的变化情况：

ppn = Perceptron(eta=0.1, n_iter=10)
ppn.fit(X, y)
plt.plot(range(1, 1 + len(ppn.J_), ppn.J_, marker='o')
plt.xlabel('epochs')
plt.ylabel('# of iterations')
plt.show()

收敛效果图：

可视化：

from matplotlib.colors import ListedColormap

def plot_decision_regions(X, y, classifier, res=0.02):
    markers = ('s', 'o', 'x', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    colormap = ListedColormap(colors[:len(np.unique(y))])

    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, res), 
                        np.arange(x2_min, x2_max, res))
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    # xx1.ravel() 将xx1从numpy.narray类型的多维素组转换为一位数组
    Z = Z.reshpae(xx1.shape())
    np.contourf(xx1, xx2, Z, alpha=.4, cmap=colormap)
    plt.xlim(x1_min, x1_max)
    plt.ylim(x2_max, x2_max)

    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y==cl, 0], y=X[y==cl, 1], marker=markers[idx],
                    alpha=.8, cmap=colormap(idx), 
                    label=np.where(cl==1, 'versicolor', 'setosa'))
ppn = Perceptron(eta=0.1, n_iter=10).fit(X, y)
plot(X, y, ppn, res=0.02)
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc='upper right')
plt.show()

5.3 平方误差之和损失函数下的感知机的梯度下降解

class AdaLine(object):
    def __init__(self, eta=0.01, n_iter=10):
        self.eta = eta
        self.n_iter = n_iter

    def fit(self, X, y):
        self.w_ = np.zeros(1+X.shape[1])        
        self.J_ = []
        for _ in range(self.n_iter):
            errors = y - self.activation(X)
            self.w_[0] += self.eta * errors.sum()
            self.w_[1:] += self.eta * X.T.dot(errors)
            J = errors.dot(errors)/2.
            self.J_.append(J)

    def net_input(self, X):
        return X.dot(self.w_[1:]) + self.w_[0]
    def activation(self, X):
        return net_input(X)
    def predict(self, X):
        return np.where(self.net_input(X) >= 0., 1, -1)

5.3.1 考察learning rate的影响

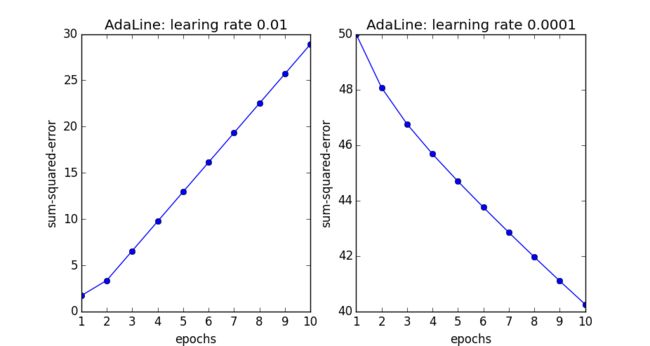
我们来考虑两个不同学习率下（ η=0.01,η=0.0001 ）的损失函数收敛情况：

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(8, 4))    # 一行两列的子图分布
ada1 = AdaLine(eta=0.01, n_iter=10).fit(X, y)
ax[0].plot(range(1, 1+len(ada1.J_)), np.log10(ada1.J_)), marker='o')
ax[0].set_xlabel('epochs')
ax[0].set_ylabel('sse')
ax[0].set_title('learning rate: 0.01')
ada2 = AdaLine(eta=0.0001, n_iter=10)
ax[1].plot(range(1, 1+len(ada2.J_)), ada2.J_, marker='o')
ax[1].set_xlabel('epochs')
ax[1].set_ylabel('sse')
ax[1].set_title('learning rate: 0.0001')
plt.show()

5.3.2 feature 标准化

在以上的两图中我们可以明显的看出，因为学习率选择的过大，损失函数错过了全局最小值，发生了发散，不再收敛（对应于左图），而学习率选择的过小，导致收敛速度很慢。

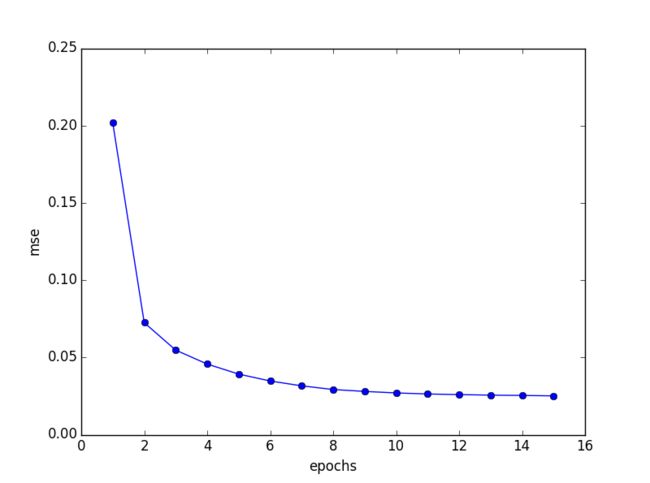
这里我们需要对输入特征进行缩放（feature scaling），或者叫标准化（standardization）：

x′j=xj−μjσj

特征的标准化工作大量地用在包括梯度下降在内的很多机器学习算法中。经标准化后的算法的执行结果如下：

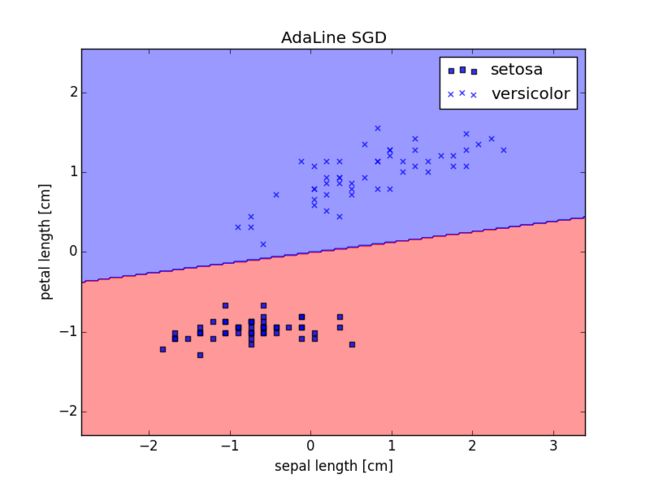
5.4 感知机的随机梯度下降解

5.3节的算法因为进行梯度更新时考虑的是一次性的将整个样本集都计算在内，

w=w+ηXT(y−XTw)

故有时也称作块梯度下降（batch gradient descent）。试想我们要处理的是一个更大规模的数据集，处理大规模数据集是机器学习算法所要面对的普遍状况。块梯度下降算法将会十分的耗时，因为每次迭代都要对整个数据集做计算。
块梯度算法的一种流行的替代方案是随机梯度下降（stochastic gradient descent），有时也叫iterative 或者 on-line gradient descent。

随机梯度下降与块梯度算法的不同在于，后者更新梯度时基于的是全部样本的加权和：

Δw=ηXT(y−Xw)

前者则是针对每一个样本，进行增量式地更新权值，即：

Δw=η(y(i)−ϕ(wTx(i)))x(i)

from numpy.random import seed

class AdaLineSGD(object):

    def __init__(self, eta=0.01, n_iter=10, shuffle=True, random_state=None):
        self.eta = eta
        self.n_iter = n_iter
        self.shuffle = shuffle
        self.w_initilized = False
        if self.shuffle:
            seed(random_state)

    def fit(self, X, y)
        self.w_ = self._initilized_weights(X.shpae[1])      
        self.J_ = []
        for _ in range(self.n_iter):
            if self.shuffle:
                X, y = self._shuffle(X, y)
            J = 0
            for xi, yi in zip(X, y):
                error = yi - self.activation(xi)
                self.w_[1:] += self.eta * error * xi
                self.w_[0] += self.eta * error
                J += error**2
            self.J_.append(J/2./len(y))
        return self 

    def net_input(self, X):
        return X.dot(self.w_[1:]) + self.w_[0]
    def activation(self, X):
        return self.net_input(X)

    def _initilized_weights(self, d):
        self.w_initilized = True
        return np.zeros(1 + d)
    def _shuffle(self, X, y):
        r = np.random.permulation(X.shape[0])
        return X[r, :], y[r]
    def predict(self, X):
        return self.net_input(X)

应用SGD算法的分类情况及损失函数的收敛情况如下：

六、 总结

algorithm	代价函数	权值更新
感知机基本形式	J=∑Ni=11y(i)≠ϕ(wTx(i))	Δw=η(y(i)−y^(i))x(i)
梯度下降	J=12∥y−Xw∥2	Δw=ηXT(y−Xw)
随机梯度下降	J=12∥y−Xw∥2	Δw=η(y(i)−ϕ(wTx(i)))x(i)