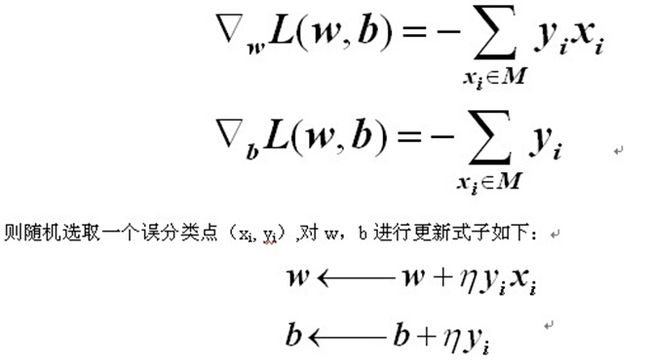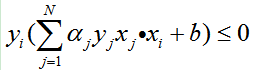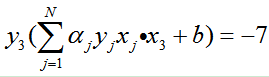感知机
概论:
感知机(perceptron)是二分类的线性分类模型 ——1957年Rosenlatt提出,神经网络与支持向量机的基础
感知机学习旨在求出将训练数据进行线性划分的分离超平面,为此,
导入基于误分类的损失函数,利用梯度下降法对损失函数进行极小化
算法分为原始形式和对偶形式
感知机预测是用学习得到的感知机模型对新的输入实例进行分类
感知机模型
f(x)=sign(w*x+b) ——w:权值、权值向量;b:偏置
sign(x)={+1,x>=0;
-1, x< 0;}
感知机的学习策略:
数据集的线性可分性:
对所有yi=+1的实例i,有w*xi+b>0;
对所有yi= -1的实例,有w*xi+b<0;
那么数据集T为线性可分数据集,否则线性不可分
感知机学习策略:
损失函数
i)损失函数的一个自然选择是误分类点的总数—但参数不是w,b的连续可导函数,不易优化
ii)误分类点到超平面S的总距离(被采用)
任一点到S的距离:
(l w*x0+b l) / ll w ll
ll w ll是w的L2范数.
其次:
对于误分类的数据(xi,yi)
-yi(w*xi+b)>0成立
所有误分类点总损失距离:
- ∑ yi(w*x1+b) / ll w ll
损失函数定义:
L(w,b)= - ∑ yi(w*x1+b) ——经验风险函数
感知机学习算法:
min L(w,b)= - ∑ yi(w*x1+b)
<strong>输入训练集T
定义学习率n(0<n<=1)
选取初值w0,b0
在训练集中选取数据(xi,yi)
如果yi(w*xi+b)<=0
</strong><span style="font-size:14px;">w+n*yi*xi→w
b+n*yi→b</span><strong>
迭代,直至没有误分类点
</strong>
算法的收敛性
novikoff定理
令S是一个非平凡的训练集,并且令:
yi( wopt *xi)=yi( wopt *xi + bopt)>=γ
woptγwopt
w opt
则 S 上在线性感知机算法的误分次数最大为:
wopt
| 迭代 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 误分 | x1 | x3 | x3 | x3 | x1 | x3 | x3 | |
| a1 | 0 | 1 | 1 | 1 | 1 | 2 | 2 | 2 |
| a2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| a3 | 0 | 0 | 1 | 2 | 3 | 3 | 4 | 5 |
| b | 0 | 1 | 0 | -1 | -2 | -1 | -2 | -3 |