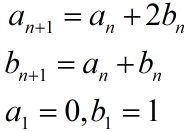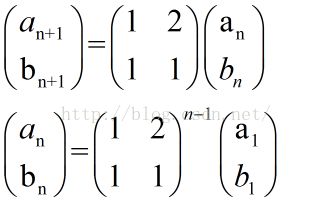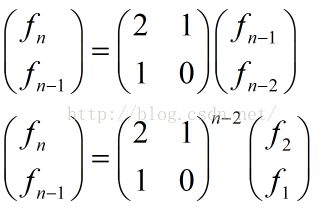- 致良知之寄诸用明书
BonSun
众所周知,当今社会,父母和社会、学校对学生的期望往往是唯分数论,包括每个人对成功的理解也往往是功名利禄,忽视了最基本的学问。文中提到,花之千叶者无实,为其华美太发露耳。人只有沉下心来,韬光养晦,才能拥有真正的学问和本领。
- Python【math数学函数】
Alan_Lowe
#Pythonpython
Python【math数学函数】文章目录Python【math数学函数】数论与表示函数1.ceil()和floor()2.comb()3.copysign()4.fabs()5.factorial()6.gcd()7.lcm()幂函数与对数函数1.exp()和math.e和pow()2.log()和log2()和log10()3.sqrt(x)三角函数1.asin、acos()、atan()2.s
- 蓝桥杯第十四届C++C组
bug~bug~
蓝桥杯蓝桥杯c++c语言
目录三国游戏填充翻转【单调队列优化DP】子矩阵【快速幂、欧拉函数】互质数的个数【tire树】异或和之差【质因数分解】公因数匹配子树的大小三国游戏题目描述小蓝正在玩一款游戏。游戏中魏蜀吴三个国家各自拥有一定数量的士兵X,Y,Z(一开始可以认为都为0)。游戏有n个可能会发生的事件,每个事件之间相互独立且最多只会发生一次,当第i个事件发生时会分别让X,Y,Z增加Ai,Bi,Ci。当游戏结束时(所有事件的
- python 实现eulers totient欧拉方程算法
luthane
算法python开发语言
eulerstotient欧拉方程算法介绍欧拉函数(Euler’sTotientFunction),通常表示为(),是一个与正整数相关的函数,它表示小于或等于的正整数中与互质的数的数目。欧拉函数在数论和密码学中有广泛的应用。欧拉函数的性质1.**对于质数,有φ(p)=p−1∗∗φ(p)=p−1^{**}φ(p)=p−1∗∗。2.**如果是质数的次幂,即n=pkn=p^kn=pk,则φ(n)=pk−
- python实现快速幂
Ronaldinho Gaúch
python算法
若需要计算a^b,如果使用循环来计算显然效率是很低的以下有三种方法实现快速幂方法一,python自带函数pow(a,b,mod),其中a为底数,b为指数,mod是对该数取模,mod参数有时候可以不传a=pow(5,9)方法二,利用递归实现快速幂,该方法需要注意分类讨论,考虑到指数为0,指数为1以及指数是奇数的情况deffast_power(a,b,mod):ifb==0:return1%modif
- 每日一题 day 08
lhsnhs
蓝桥杯职场和发展
1>递归次数过多,栈溢出emmclassSolution{publicdoublemyPow(doublex,intn){doubleans=1.0;if(n使用快速幂
- 算法设计与分析学习(6)——数论
罗塞菈桔梨萝柚
算法学习算法线性代数
数论整除基本概念若aaa和bbb为整数,且a≠0a≠0a=0若存在整数qqq使得b=aqb=aqb=aq,那么就说aaa可以整除bbb或是bbb被aaa整除,记作a∣ba|ba∣b。aaa也被称为bbb的约数,bbb也被称为a的倍数。若bbb不能被aaa整除,则记作a∤ba\not{|}ba∣b。整数p≠0,±1p≠0,±1p=0,±1,且除了±1,±p±1,±p±1,±p外没有其他的约数
- 洛谷刷题之P1226
傻傻的傻瓜
洛谷c++
【模板】快速幂题目描述给你三个整数a,b,pa,b,pa,b,p,求ab mod pa^b\bmodpabmodp。输入格式输入只有一行三个整数,分别代表a,b,pa,b,pa,b,p。输出格式输出一行一个字符串a^bmodp=s,其中a,b,pa,b,pa,b,p分别为题目给定的值,sss为运算结果。样例#1样例输入#12109样例输出#12^10mod9=7提示样例解释210=10242^{1
- 数论——欧几里得算法
NarutoTime
数论算法c++数据结构c语言
1.欧几里得简介 欧几里得(希腊文:Ευκλειδης,约公元前330年—公元前275年),古希腊数学家,被称为“几何之父”。他最著名的著作《几何原本》是欧洲数学的基础,在书中他提出五大公设。欧几里得的《几何原本》被广泛的认为是历史上最成功的教科书。欧几里得也写了一些关于透视、圆锥曲线、球面几何学及数论的作品。2.欧几里得算法欧几里得算法用于:求解a和b的最大公约数。最大公约数英文为:Gre
- 数论——扩展欧几里得算法
NOI_yzk
欧几里得&拓展欧几里得(Euclid&Extend-Euclid)欧几里得算法(Euclid)背景:欧几里德算法又称辗转相除法,用于计算两个正整数a,b的最大公约数。——百度百科代码:递推的代码是相当的简洁:intgcd(inta,intb){returnb==0?a:gcd(b,a%b);}分析:方法说了是辗转相除法,自然没有什么好介绍的了。。Fresh肯定会觉得这样递归下去会不会爆栈?实际上在
- 数论学习1(欧几里德算法+唯一分解定理+埃氏筛+拓展欧几里德+同余与模算术)
new出新对象!
数学数算法学习
目录1.唯一分解定理2.欧几里德算法(求最大公约数)3.求最小公倍数4.埃氏筛5.拓展欧几里德算法(1)证明一下线性方程组的正数的最小值是多少,(2)如何通过裴蜀定理退出拓展欧几里得算法(贝祖定理)6.同余与模算术(1)取模运算操作加法取模运算减法取模运算乘法取模运算(2)特殊的取模操作大整数取模幂取模(3)同余式,乘法逆元,费马小定理今天也是小小的开始学习数论方面的知识了,首先数论的入门章节必然
- 一些简单却精妙的算法
写代码的大学生
算法
文章目录1.树状数组2.红黑树3.星星打分4.欧几里得算法5.快速幂6.并查集在编程的世界里,简洁的代码往往隐藏着深邃的智慧。一起来看看那些看似简单,实则精妙绝伦的代码片段,体会编程语言的优雅与力量。1.树状数组intlowbit(intx){returnx&-x;}树状数组里的这个,太精妙了,树状数组使区间求和复杂度降低到了log(n),发明这段代码的人一定是个天才,而这个lowbit恰恰是最精
- Collatz 猜想和 Python
不连续小姐
PythonDay4:CollatzConjecture原来总有学生问我,微积分有什么用啊,我说如果微积分学好了,也许抽象代数和数论就能学好,那最后就能像AndrewWiles一样上人物年度杂志的封面了.(AndrewWiles证明了Fermat'sLastTheorem,费玛大定理).[captionid="attachment_1466"align="alignnone"width="300"
- 【数据结构与算法】从左到右快速幂和从右到左快速幂
星眺北海
数据结构与算法算法快速幂
引出问题在计算机科学中,幂运算是一种非常常见且基础的操作,尤其是在涉及到大数运算时,幂运算的效率对整个计算过程至关重要。设想以下场景:在加密算法中,如RSA算法,常常需要计算大数的幂,且这种计算必须在一定时间内完成,以确保安全性。在数值计算中,我们可能需要反复进行大规模的幂运算,如果采用最直接的计算方法,其计算量和时间将非常庞大。如果我们采用朴素的计算方法,例如计算aba^bab时,通过不断相乘a
- 初等数论--整除--带余除法
WeidanJi
初等数论数学密码学信息安全
初等数论--整除--带余除法概念基本性质带余除法博主本人是初学初等数论(整除+同余+原根),本意是想整理一些较难理解的定理、算法,加深记忆也方便日后查找;如果有错,欢迎指正。我整理成一个系列:初等数论,方便检索。概念初等数论研究对象是整数集合和自然数集合。初等数论研究对象是整数集合和自然数集合。初等数论研究对象是整数集合和自然数集合。b∣a:若a,b∈Z,b≠0,∃c∈Z,使a=bc,则称b整除a
- 河南萌新联赛2024第(一)场:河南农业大学
FS_tar
算法c++数据结构排序算法
河南萌新联赛2024第(一)场:河南农业大学2024.7.1713:00————15:00过题数6/12补题数8/12造数爱探险的朵拉有大家喜欢的零食吗小蓝的二进制询问奇妙的脑回路两难抉择新编旅途的终点两难抉择除法移位最大矩阵匹配图上计数(Easy)图上计数(Hard)A-造数其实题不难,但是可能脑子没转,所以没有想到逆向思维,wa了3发还很影响心态。亏我甚至还搞了个快速幂,一点关系没有。题解:给
- 河南萌新2024第四场
Pown_ShanYu
算法数据结构
C岗位分配题目大意:有n个岗位,m位志愿者,每个岗位至少需要a个志愿者,并且可以有志愿者可以空闲下来作预备,给出可能的分配情况总数思路:首先将每个岗位分配好至少需要的志愿者,再将剩下的人进行分配,那就满足球同盒不同模型(允许空盒),可用隔板法进行分配,需要额外开设一个空闲岗位用来预备,那么按照4个人去4个岗位,那么为c73,具体操作可看数论模板中发布的隔板法问题,递归求组合数Solved:intn
- 【读书笔记】吴非《致青年教师》(4)
冬儿菇凉
一、精要摘录(48——106页)1.教育教学不能“唯分数论“,比分数重要的是学生思维品质和解决实际问题的能力。2.一名教师心中有使命感,心中有学生才会很在意学生对他的态度,在意学生的接受度。3.作为教师,你要善于向学生问出有意思的问题。4.教育就是要培养好习惯,教是为了达到不需要教学生,不需要老师教了是教学的成功,也是教师的职业追求。5.教师是学习者,在学习上教师首先要郑重其事,学生才有可能养成敬
- 数学知识——欧拉函数、快速幂、扩展欧几里得算法
up-to-star
acwing算法基础课学习笔记
欧拉函数欧拉函数定义为ϕ(n)=1−n中与n互质的个数\phi(n)=1-n中与n互质的个数ϕ(n)=1−n中与n互质的个数,互质就是最大公约数是1。欧拉函数求解公式:将n分解质因数:n=p1a1+p2a2+...+pkakn=p_1^{a1}+p_2^{a2}+...+p_k^{ak}n=p1a1+p2a2+...+pkak,则ϕ(n)=n∗(1−1p1)∗(1−1p2)∗.....∗(1−1p
- 【快速幂、欧拉函数】蓝桥杯第十四届---互质数的个数
bug~bug~
蓝桥杯蓝桥杯职场和发展
给定a,b,求1≤xusingnamespacestd;typedeflonglongLL;constintmod=998244353;LLquick_pow(LLa,LLb){LLres=1;while(b){if(b&1)res=res*a%mod;a=a*a%mod;b>>=1;}returnres;}LLeu(LLn){LLres=n;for(LLi=2;i1)res=res*(n-1)/
- 【欧拉函数+快速幂】第十四届蓝桥杯省赛C++ C组 Java A组/研究生组 Python 研究生组《互质数的个数》(C++)
北洋的霞洛
蓝桥杯历年真题蓝桥杯c++算法模板方法模式
【题目描述】给定a,b,求1≤x#include#includeusingnamespacestd;typedeflonglongLL;constintMOD=998244353;LLqmi(LLa,LLb){LLres=1;while(b){if(b&1)res=res*a%MOD;a=a*a%MOD;b>>=1;}returnres;}intmain(){LLa,b;cin>>a>>b;if(
- 基础算法(二)#蓝桥杯
席万里
C/C++备战蓝桥杯算法蓝桥杯c++
文章目录8、双指针8.1、挑选子串8.2、聪明的小羊肖恩8.3、神奇的数组9、二分9.1、跳石头9.2、可凑成的最大花朵数9.3、最大通过数9.4、妮妮的月饼广场9.5、基德的神秘冒险9.6、体育健将10、倍增10.1、快速幂10.2、最近公共祖先LCA查询10.3、理想之城10.4、数的变换8、双指针8.1、挑选子串#include#defineIOSios::sync_with_stdio(f
- 【代码随想录算法训练营Day39】62.不同路径;63. 不同路径 II
想做一只潜水的猪
算法
文章目录❇️Day39第九章动态规划part02✴️今日任务❇️62.不同路径自己的思路自己的代码随想录思路随想录代码❇️63.不同路径II自己的思路自己的代码随想录代码❇️Day39第九章动态规划part02✴️今日任务今天开始逐渐有dp的感觉了,题目不多,就两个不同路径,可以好好研究一下62.不同路径63.不同路径II❇️62.不同路径本题大家掌握动态规划的方法就可以。数论方法有点非主流,很难
- 算法D39 | 动态规划2 | 62.不同路径 63. 不同路径 II
memolaner
算法训练营算法动态规划数据结构c++python
今天开始逐渐有dp的感觉了,题目不多,就两个不同路径,可以好好研究一下62.不同路径本题大家掌握动态规划的方法就可以。数论方法有点非主流,很难想到。代码随想录视频讲解:动态规划中如何初始化很重要!|LeetCode:62.不同路径_哔哩哔哩_bilibili这个题看到路径的表示,第一直觉就是一个组合数的问题,学了一下C++计算组合数防止溢出的小技巧。第二个方法再动态规划完成,重点是把二维的动态规划
- 牛客周赛 Round 35(A,B,C,D,E,F,G)
邪神与厨二病
牛客算法暴力c++数论滑动窗口单调队列贪心构造
这场简单,甚至赛时90分钟不到就AK了。比赛链接,队友题解友链刚入住学校监狱,很不适应,最近难受的要死,加上最近几场CF打的都不顺利,san值要爆掉了,只能慢慢补题了。这场C是个滑动窗口,D是贪心,E是有点麻烦的构造,FG是数论。A小红的字符串切割思路:记录一下字符串长度,然后从中间拆开。code:#include#include#includeusingnamespacestd;strings;
- 牛客寒假基础集训营 | 技巧总结
大虎牙
#牛客寒假基础集训营牛客寒假基础集训营牛客技巧
自己思考,用笔划划,用心理解算法,不要先看代码做一道题,会一道题,追求解题质量,不要贪恋速度举一反三举具体例子,便于理解,捋清思路Day1技巧使用vector数组存储字符串中不同字符的下标。双指针思想,滑动窗口。字符串问题中,使用数组存储动态规划思想的值。Day2技巧缩小范围至开根号快速幂、位运算longlong存不下,素数1e9+7取模Day3技巧埃式筛判断素数用空间换时间,定义很大长度的数组存
- 算法——数论——同余
戏拈秃笔
数据结构与算法(java版)算法
目录同余一、试题算法训练同余方程同余同余使人们能够用等式的形式简洁地描述整除关系同余:若m(正整数),a和b是整数,a%m==b%m,或(a-b)%m==0,记为ab(modm)求解一元线性同余方程等价于求解二元线性丢番图方程一元线性同余方程,解法看下面第一题二元线性丢番图方程逆:的一个解为a模m的逆一、试题算法训练同余方程问题描述求关于x的同余方程ax≡1(modb)的最小正整数解。输入格式输入
- pku acm 题目分类
moxiaomomo
算法数据结构numbers优化calendarcombinations
1.搜索//回溯2.DP(动态规划)3.贪心北大ACM题分类2009-01-2714.图论//Dijkstra、最小生成树、网络流5.数论//解模线性方程6.计算几何//凸壳、同等安置矩形的并的面积与周长sp;7.组合数学//Polya定理8.模拟9.数据结构//并查集、堆sp;10.博弈论1、排序sp;1423,1694,1723,1727,1763,1788,1828,1838,1840,22
- C++STL之Queue容器
芯片烧毁大师
数据结构C++c++开发语言
C++STL之Queue容器1.再谈队列回顾一下之前所学的队列,队列和栈不同,队列是一种先进先出的数据结构,STL的队列内容极其重要,虽然内容较少但是请务必掌握,STL的队列是快速构建搜索算法以及相关的数论图论的状态存储的基础。2.相关头文件头文件:#include3.初始化格式为:**explicit**queue(**const**container_type&ctnr=container_t
- 动态DP入门&线性动态DP
罗博士
ACM动态规划动态规划算法ACM
动态DP入门&线性动态DP前言核心思想例1例22024牛客寒假4K2022牛客寒假2J结论前言OI-WiKi上有一个动态DP讲解,直接讲到了树型DP领域,同时需要树链剖分,门槛有点高。本文针对线性DP做一个动态DP的讲解。首先当然要懂得一定的DP的相关知识,然后需要知道DP方程的矩阵表达。可以看这里——根据递推公式构造系数矩阵用于快速幂。很多DP的状态转移方程都可以写成矩阵形式,由此就有了矩阵快速
- 二分查找排序算法
周凡杨
java二分查找排序算法折半
一:概念 二分查找又称
折半查找(
折半搜索/
二分搜索),优点是比较次数少,查找速度快,平均性能好;其缺点是要求待查表为有序表,且插入删除困难。因此,折半查找方法适用于不经常变动而 查找频繁的有序列表。首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表 分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步
- java中的BigDecimal
bijian1013
javaBigDecimal
在项目开发过程中出现精度丢失问题,查资料用BigDecimal解决,并发现如下这篇BigDecimal的解决问题的思路和方法很值得学习,特转载。
原文地址:http://blog.csdn.net/ugg/article/de
- Shell echo命令详解
daizj
echoshell
Shell echo命令
Shell 的 echo 指令与 PHP 的 echo 指令类似,都是用于字符串的输出。命令格式:
echo string
您可以使用echo实现更复杂的输出格式控制。 1.显示普通字符串:
echo "It is a test"
这里的双引号完全可以省略,以下命令与上面实例效果一致:
echo Itis a test 2.显示转义
- Oracle DBA 简单操作
周凡杨
oracle dba sql
--执行次数多的SQL
select sql_text,executions from (
select sql_text,executions from v$sqlarea order by executions desc
) where rownum<81;
&nb
- 画图重绘
朱辉辉33
游戏
我第一次接触重绘是编写五子棋小游戏的时候,因为游戏里的棋盘是用线绘制的,而这些东西并不在系统自带的重绘里,所以在移动窗体时,棋盘并不会重绘出来。所以我们要重写系统的重绘方法。
在重写系统重绘方法时,我们要注意一定要调用父类的重绘方法,即加上super.paint(g),因为如果不调用父类的重绘方式,重写后会把父类的重绘覆盖掉,而父类的重绘方法是绘制画布,这样就导致我们
- 线程之初体验
西蜀石兰
线程
一直觉得多线程是学Java的一个分水岭,懂多线程才算入门。
之前看《编程思想》的多线程章节,看的云里雾里,知道线程类有哪几个方法,却依旧不知道线程到底是什么?书上都写线程是进程的模块,共享线程的资源,可是这跟多线程编程有毛线的关系,呜呜。。。
线程其实也是用户自定义的任务,不要过多的强调线程的属性,而忽略了线程最基本的属性。
你可以在线程类的run()方法中定义自己的任务,就跟正常的Ja
- linux集群互相免登陆配置
林鹤霄
linux
配置ssh免登陆
1、生成秘钥和公钥 ssh-keygen -t rsa
2、提示让你输入,什么都不输,三次回车之后会在~下面的.ssh文件夹中多出两个文件id_rsa 和 id_rsa.pub
其中id_rsa为秘钥,id_rsa.pub为公钥,使用公钥加密的数据只有私钥才能对这些数据解密 c
- mysql : Lock wait timeout exceeded; try restarting transaction
aigo
mysql
原文:http://www.cnblogs.com/freeliver54/archive/2010/09/30/1839042.html
原因是你使用的InnoDB 表类型的时候,
默认参数:innodb_lock_wait_timeout设置锁等待的时间是50s,
因为有的锁等待超过了这个时间,所以抱错.
你可以把这个时间加长,或者优化存储
- Socket编程 基本的聊天实现。
alleni123
socket
public class Server
{
//用来存储所有连接上来的客户
private List<ServerThread> clients;
public static void main(String[] args)
{
Server s = new Server();
s.startServer(9988);
}
publi
- 多线程监听器事件模式(一个简单的例子)
百合不是茶
线程监听模式
多线程的事件监听器模式
监听器时间模式经常与多线程使用,在多线程中如何知道我的线程正在执行那什么内容,可以通过时间监听器模式得到
创建多线程的事件监听器模式 思路:
1, 创建线程并启动,在创建线程的位置设置一个标记
2,创建队
- spring InitializingBean接口
bijian1013
javaspring
spring的事务的TransactionTemplate,其源码如下:
public class TransactionTemplate extends DefaultTransactionDefinition implements TransactionOperations, InitializingBean{
...
}
TransactionTemplate继承了DefaultT
- Oracle中询表的权限被授予给了哪些用户
bijian1013
oracle数据库权限
Oracle查询表将权限赋给了哪些用户的SQL,以备查用。
select t.table_name as "表名",
t.grantee as "被授权的属组",
t.owner as "对象所在的属组"
- 【Struts2五】Struts2 参数传值
bit1129
struts2
Struts2中参数传值的3种情况
1.请求参数绑定到Action的实例字段上
2.Action将值传递到转发的视图上
3.Action将值传递到重定向的视图上
一、请求参数绑定到Action的实例字段上以及Action将值传递到转发的视图上
Struts可以自动将请求URL中的请求参数或者表单提交的参数绑定到Action定义的实例字段上,绑定的规则使用ognl表达式语言
- 【Kafka十四】关于auto.offset.reset[Q/A]
bit1129
kafka
I got serveral questions about auto.offset.reset. This configuration parameter governs how consumer read the message from Kafka when there is no initial offset in ZooKeeper or
- nginx gzip压缩配置
ronin47
nginx gzip 压缩范例
nginx gzip压缩配置 更多
0
nginx
gzip
配置
随着nginx的发展,越来越多的网站使用nginx,因此nginx的优化变得越来越重要,今天我们来看看nginx的gzip压缩到底是怎么压缩的呢?
gzip(GNU-ZIP)是一种压缩技术。经过gzip压缩后页面大小可以变为原来的30%甚至更小,这样,用
- java-13.输入一个单向链表,输出该链表中倒数第 k 个节点
bylijinnan
java
two cursors.
Make the first cursor go K steps first.
/*
* 第 13 题:题目:输入一个单向链表,输出该链表中倒数第 k 个节点
*/
public void displayKthItemsBackWard(ListNode head,int k){
ListNode p1=head,p2=head;
- Spring源码学习-JdbcTemplate queryForObject
bylijinnan
javaspring
JdbcTemplate中有两个可能会混淆的queryForObject方法:
1.
Object queryForObject(String sql, Object[] args, Class requiredType)
2.
Object queryForObject(String sql, Object[] args, RowMapper rowMapper)
第1个方法是只查
- [冰川时代]在冰川时代,我们需要什么样的技术?
comsci
技术
看美国那边的气候情况....我有个感觉...是不是要进入小冰期了?
那么在小冰期里面...我们的户外活动肯定会出现很多问题...在室内呆着的情况会非常多...怎么在室内呆着而不发闷...怎么用最低的电力保证室内的温度.....这都需要技术手段...
&nb
- js 获取浏览器型号
cuityang
js浏览器
根据浏览器获取iphone和apk的下载地址
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8" content="text/html"/>
<meta name=
- C# socks5详解 转
dalan_123
socketC#
http://www.cnblogs.com/zhujiechang/archive/2008/10/21/1316308.html 这里主要讲的是用.NET实现基于Socket5下面的代理协议进行客户端的通讯,Socket4的实现是类似的,注意的事,这里不是讲用C#实现一个代理服务器,因为实现一个代理服务器需要实现很多协议,头大,而且现在市面上有很多现成的代理服务器用,性能又好,
- 运维 Centos问题汇总
dcj3sjt126com
云主机
一、sh 脚本不执行的原因
sh脚本不执行的原因 只有2个
1.权限不够
2.sh脚本里路径没写完整。
二、解决You have new mail in /var/spool/mail/root
修改/usr/share/logwatch/default.conf/logwatch.conf配置文件
MailTo =
MailFrom
三、查询连接数
- Yii防注入攻击笔记
dcj3sjt126com
sqlWEB安全yii
网站表单有注入漏洞须对所有用户输入的内容进行个过滤和检查,可以使用正则表达式或者直接输入字符判断,大部分是只允许输入字母和数字的,其它字符度不允许;对于内容复杂表单的内容,应该对html和script的符号进行转义替换:尤其是<,>,',"",&这几个符号 这里有个转义对照表:
http://blog.csdn.net/xinzhu1990/articl
- MongoDB简介[一]
eksliang
mongodbMongoDB简介
MongoDB简介
转载请出自出处:http://eksliang.iteye.com/blog/2173288 1.1易于使用
MongoDB是一个面向文档的数据库,而不是关系型数据库。与关系型数据库相比,面向文档的数据库不再有行的概念,取而代之的是更为灵活的“文档”模型。
另外,不
- zookeeper windows 入门安装和测试
greemranqq
zookeeper安装分布式
一、序言
以下是我对zookeeper 的一些理解: zookeeper 作为一个服务注册信息存储的管理工具,好吧,这样说得很抽象,我们举个“栗子”。
栗子1号:
假设我是一家KTV的老板,我同时拥有5家KTV,我肯定得时刻监视
- Spring之使用事务缘由(2-注解实现)
ihuning
spring
Spring事务注解实现
1. 依赖包:
1.1 spring包:
spring-beans-4.0.0.RELEASE.jar
spring-context-4.0.0.
- iOS App Launch Option
啸笑天
option
iOS 程序启动时总会调用application:didFinishLaunchingWithOptions:,其中第二个参数launchOptions为NSDictionary类型的对象,里面存储有此程序启动的原因。
launchOptions中的可能键值见UIApplication Class Reference的Launch Options Keys节 。
1、若用户直接
- jdk与jre的区别(_)
macroli
javajvmjdk
简单的说JDK是面向开发人员使用的SDK,它提供了Java的开发环境和运行环境。SDK是Software Development Kit 一般指软件开发包,可以包括函数库、编译程序等。
JDK就是Java Development Kit JRE是Java Runtime Enviroment是指Java的运行环境,是面向Java程序的使用者,而不是开发者。 如果安装了JDK,会发同你
- Updates were rejected because the tip of your current branch is behind
qiaolevip
学习永无止境每天进步一点点众观千象git
$ git push joe prod-2295-1
To
[email protected]:joe.le/dr-frontend.git
! [rejected] prod-2295-1 -> prod-2295-1 (non-fast-forward)
error: failed to push some refs to '
[email protected]
- [一起学Hive]之十四-Hive的元数据表结构详解
superlxw1234
hivehive元数据结构
关键字:Hive元数据、Hive元数据表结构
之前在 “[一起学Hive]之一–Hive概述,Hive是什么”中介绍过,Hive自己维护了一套元数据,用户通过HQL查询时候,Hive首先需要结合元数据,将HQL翻译成MapReduce去执行。
本文介绍一下Hive元数据中重要的一些表结构及用途,以Hive0.13为例。
文章最后面,会以一个示例来全面了解一下,
- Spring 3.2.14,4.1.7,4.2.RC2发布
wiselyman
Spring 3
Spring 3.2.14、4.1.7及4.2.RC2于6月30日发布。
其中Spring 3.2.1是一个维护版本(维护周期到2016-12-31截止),后续会继续根据需求和bug发布维护版本。此时,Spring官方强烈建议升级Spring框架至4.1.7 或者将要发布的4.2 。
其中Spring 4.1.7主要包含这些更新内容。