暑假集训第二周——递推 汉诺塔系列问题

/先说汉若塔I（经典汉若塔问题），有三塔，A塔从小到大从上至下放有N个盘子，现在要搬到目标C上，

规则小的必需放在大的上面，每次搬一个，求最小步数。这个问题简单，DP：a[n]=a[n-1]+1+a[n-1],先把

上面的n-1个放在B上，把最大的放在目标C上，再把N-1个放回到C上即可

B - 汉诺塔II

Time Limit:1000MS     Memory Limit:32768KB     64bit IO Format:%I64d & %I64u

Submit  Status

Description

经典的汉诺塔问题经常作为一个递归的经典例题存在。可能有人并不知道汉诺塔问题的典故。汉诺塔来源于印度传说的一个故事，上帝创造世界时作了三根金刚石柱子，在一根柱子上从下往上按大小顺序摞着64片黄金圆盘。上帝命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一回只能移动一个圆盘。有预言说，这件事完成时宇宙会在一瞬间闪电式毁灭。也有人相信婆罗门至今仍在一刻不停地搬动着圆盘。恩，当然这个传说并不可信，如今汉诺塔更多的是作为一个玩具存在。Gardon就收到了一个汉诺塔玩具作为生日礼物。 
　　Gardon是个怕麻烦的人（恩，就是爱偷懒的人），很显然将64个圆盘逐一搬动直到所有的盘子都到达第三个柱子上很困难，所以Gardon决定作个小弊，他又找来了一根一模一样的柱子，通过这个柱子来更快的把所有的盘子移到第三个柱子上。下面的问题就是：当Gardon在一次游戏中使用了N个盘子时，他需要多少次移动才能把他们都移到第三个柱子上？很显然，在没有第四个柱子时，问题的解是2^N-1，但现在有了这个柱子的帮助，又该是多少呢？ 

 

Input

包含多组数据，每个数据一行，是盘子的数目N(1<=N<=64)。 

 

Output

对于每组数据，输出一个数，到达目标需要的最少的移动数。 

 

Sample Input

      
      
      
      

       
       
       
       1
3
12 
      
      
      
      

 

Sample Output

      
      
      
      

       
       
       
       1
5
81 
      
      
      
      

动态规划，转移是

g[n]=min{g[n-k]+g[n-k]+f[k]}(1<=k<n)其中f[n]是三个柱子时候的汉诺塔

f[n]=f[n-1]+f[n-1]+1;----->f[n]=2^n-1;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

#include<stdio.h>
#include<math.h>
int main()
{
  int n,i,k,f[65],m;
  f[1]=1,f[2]=3;
  for(i=3;i<=65;i++)
  {
      m=99999999;
      for(k=1;k<i;k++)
  if(2*f[k]+pow(2,i-k)-1<m)
    m=2*f[k]+(int)pow(2,i-k)-1;
  f[i]=m;
  }
  while(scanf("%d",&n)!=EOF)
    printf("%d\n",f[n]);
    return 0;
}

汉若塔III  hdu2064

Description

约19世纪末，在欧州的商店中出售一种智力玩具，在一块铜板上有三根杆，最左边的杆上自上而下、由小到大顺序串着由64个圆盘构成的塔。目的是将最左边杆上的盘全部移到右边的杆上，条件是一次只能移动一个盘，且不允许大盘放在小盘的上面。
现在我们改变游戏的玩法，不允许直接从最左(右)边移到最右(左)边(每次移动一定是移到中间杆或从中间移出)，也不允许大盘放到下盘的上面。 
Daisy已经做过原来的汉诺塔问题和汉诺塔II，但碰到这个问题时，她想了很久都不能解决，现在请你帮助她。现在有N个圆盘，她至少多少次移动才能把这些圆盘从最左边移到最右边？ 

 

Input

包含多组数据，每次输入一个N值(1<=N=35)。

 

Output

对于每组数据，输出移动最小的次数。

 

Sample Input

     
     
     
     

      
      
      
      1
3
12 
     
     
     
     

 

Sample Output

     
     
     
     

      
      
      
      2
26
531440 
     
     
     
     

在经典汉若塔问题的条件改为，每次只能移动到附近塔上，求把A塔所有的移动C塔最小次数。

a[n]=a[n-1]+1+a[n-1]+1+a[n-1]:先把上面的N-1个移动到C(必然有这个状态)，在把最大的移到B，再把N-1移到到A，把最大的移到C，再把N-1个移到C。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<iostream>
#include<cmath>
using namespace std;
unsigned long long a[65];
int main()
{
  a[1]=2;
  for(int i=2;i<36;i++)
  {
    a[i]=3*a[i-1]+2;
  }
  int n;
  while(cin>>n)
  {
    cout<<a[n]<<endl;
  }
  return 0;
}

汉若塔IV HDU 2077

IV 

Time Limit:1000MS     Memory Limit:32768KB     64bit IO Format:%I64d & %I64u

Submit  Status

Description

还记得汉诺塔III吗？他的规则是这样的：不允许直接从最左(右)边移到最右(左)边(每次移动一定是移到中间杆或从中间移出)，也不允许大盘放到小盘的上面。xhd在想如果我们允许最大的盘子放到最上面会怎么样呢？（只允许最大的放在最上面）当然最后需要的结果是盘子从小到大排在最右边。 

 

Input

输入数据的第一行是一个数据T，表示有T组数据。 
每组数据有一个正整数n(1 <= n <= 20)，表示有n个盘子。 

 

Output

对于每组输入数据，最少需要的摆放次数。 

 

Sample Input

      
      
      
      

       
       
       
       2 1 10 
      
      
      
      

 

Sample Output

      
      
      
      

       
       
       
       2 19684 
      
      
      
      

 

分析：

A,B,C三个塔，方程：a[n]=ab[n-1]+1+1+bc[n-1]. (ab表示a到b)

DP思路：先把n-1个搬到b,再用俩步般最大的到C，再把n-1个从B到C。这里又要求出ac[n]和bc[n]：求其递推方程：bc[n]=bc[n-1]+1+ac[n-1]，

会发现bc[]方程和ab[n]一样的。所以总方程a[n]=2*ab[n-1]+2.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

#include<iostream>
#include<cmath>
using namespace std;
long long ac[23],bc[23],a[23];
int main()
{
    ac[1]=a[1]=2,bc[1]=1,a[2]=4;
    int i,t,n;
    for(i=2;i<22;i++)
{
         ac[i]=3*ac[i-1]+2;
    bc[i]=bc[i-1]+1+ac[i-1];
}

for(i=3;i<22;i++)
    a[i]=2*bc[i-1]+2;
cin>>t;
while(t--)
{
    cin>>n;
    cout<<a[n]<<endl;
}
return 0;
}

I - 汉诺塔V

Time Limit:1000MS     Memory Limit:32768KB     64bit IO Format:%I64d & %I64u

Submit  Status

Description

n个盘子的汉诺塔问题的最少移动次数是2^n-1,即在移动过程中会产生2^n个系列。由于 
发生错移产生的系列就增加了，这种错误是放错了柱子，并不会把大盘放到小盘上，即各柱 
子从下往上的大小仍保持如下关系 ： 
n=m+p+q 
a1>a2>...>am 
b1>b2>...>bp 
c1>c2>...>cq 
计算所有会产生的系列总数. 

 

Input

包含多组数据，首先输入T,表示有T组数据.每个数据一行，是盘子的数 
目N<30.

 

Output

对于每组数据，输出移动过程中所有会产生的系列总数。

 

Sample Input

      
      
      
      

       
       
       
       3 1 3 29 
      
      
      
      

 

Sample Output

      
      
      
      

       
       
       
       3 27 68630377364883 
      
      
      
      

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

#include<stdio.h>
int main()
{
    int t,n,i;
    long long  a[30];
    scanf("%d",&t);
    while(t--)
    {
        a[0]=1;
        scanf("%d",&n);
        for(i=1;i<=n;i++)
            a[i]=3*a[i-1];
        printf("%lld\n",a[n]);
    }
    return 0;
}

汉若塔VI HDU1995

在经典汉若塔问题上附加问题：求出N个盘子时，第K号盘子的移动次数。

思路，一想就是二维DP，DP[n][i]=dp[n-1][i]*2(1=<i<n),dp[n][n]=1;

最大盘只移动一次，上面盘子先移到B塔，一次，最后由B到目标C又一次，思路清晰，分分钟KO。

#include<iostream>
#include<cmath>
using namespace std;
unsigned long long dp[62][62];
int main()
{
  dp[1][1]=1;dp[2][1]=2;dp[2][2]=1;
  for(int i=3;i<61;i++)
  {
     for(int j=1;j<i;j++)
     {
       dp[i][j]=2*dp[i-1][j];
     }
     dp[i][i]=1;
  }
  int t;
  int n,m;
  cin>>t;
  while(t--)
  {
    cin>>n>>m;
    cout<<dp[n][m]<<endl;
  }
  return 0;
}

汉若塔VII HDU1996

在经典汉若塔问题上，求一共有多少个状态（包括所有可能移到到的状态），一个排列组合问题，

答案：求和（ C(k1,n)*C(k2,n-k1)）其中n>=k1>=0,n-k1>=K2>=0,从中挑出K1个从小到大放在A塔，再从剩下的

挑出K2个放在B塔，剩余的放在C塔即可。数据非大数。

其他巧妙方法：每个盘从小到大每个都有3种选择，共3^n。

#include<iostream>
using namespace std;
unsigned long long a[32];
long long C(int m,int n)  //M>=N
{
  if(m==0||n==0)return 1;
     int i;
     long long c=1,s=1;
     if(n>m-n)
     {
        n=m-n;
     }
     for(i=m;i>=m-n+1;i--)
     {
       c=c*i;
     }
     for(i=n;i>1;i--)
     {
       s*=i;
    }

     c=c/s;
     return c;
}
int main()
{
  for(int i=1;i<30;i++)
  {
     for(int k1=0;k1<=i;k1++)
     {
      for(int k2=0;k2<=i-k1;k2++)
       {
         a[i]+=C(i,k1)*C(i-k1,k2);
       }
     }
  }
  int t;
  int n,m;
  cin>>t;
  while(t--)
  {
    cin>>n;
    cout<<a[n]<<endl;
  }
  return 0;
}

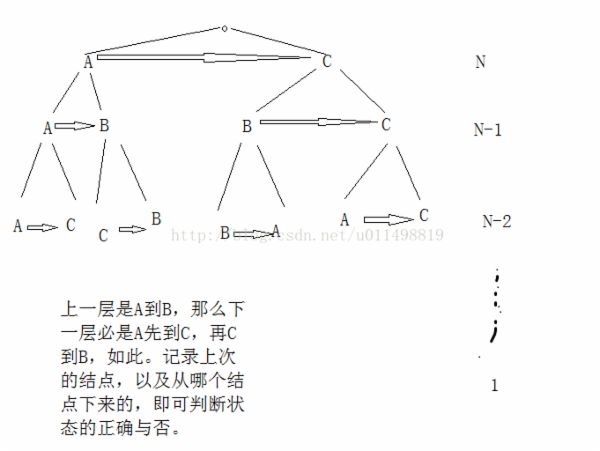
汉诺塔VII hdu1997 在经典汉若塔问题上，给出任意一个状态（移到过程中），判断该状态是否在正确的（最小移到情况）状态

中。

思路：做到这题，汉若塔就很清晰了，有几步、几个状态、状态的正确性、每个盘子的移到情况，都了如指掌。说说该题思路：

n号塔必然是A->C，那么N-1号塔， 若n在A，则n-1 在A或B，

见图：

#include<iostream>
using namespace std;
char get[68];		   //保存I号盘子在哪个塔
bool over=0; bool tf=1;  //是否结束，true_or_false是否为假
void dfs(char fl,char fr, char cur,int now)  // dfs ，上面一层（now）左边和右边的塔，已经从哪个塔“下来的”（上面一层是哪个塔）
{
  if(over)return;
  if(now==1){over=1;return;}  //出口
  int temp;
  if(fl=='A'&&fr=='B'||fl=='B'&&fr=='A')temp='C';
  else if(fl=='A'&&fr=='C'||fl=='C'&&fr=='A')temp='B';
  else temp='A';
  now--;
  if(cur==fl)   //若上一层是左边的塔
  {
    if(get[now]==fr){over=1;tf=0;return;}  //不可能是fr
    else
    {
      dfs(fl,temp,get[now],now);  
    }
  }
  else if(cur==fr)
  {
    if(get[now]==fl){over=1;tf=0;return;}
    else
    {
      dfs(temp,fr,get[now],now);
    }
  }
}
int main()
{
  int T;
  cin>>T;
  while(T--)
  {
    int n,m,p,q,tx;
    cin>>n;
    cin>>m;
    for(int i=0;i<m;i++)
    {
      cin>>tx;get[tx]='A';
    }
    cin>>p;
    for(int i=0;i<p;i++)
    {
      cin>>tx;get[tx]='B';
    }
    cin>>q;
    for(int i=0;i<q;i++)
    {
      cin>>tx;get[tx]='C';
    }
    tf=1;
    over=0;
    if(get[n]=='B')
    {
      cout<<"false"<<endl;continue;
    }
    dfs('A','C',get[n],n);
    if(tf==1)cout<<"true"<<endl;
    else cout<<"false"<<endl;
  }
  return 0;
}