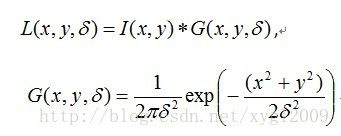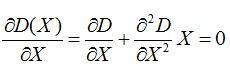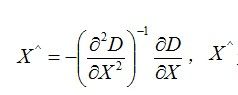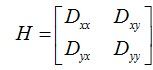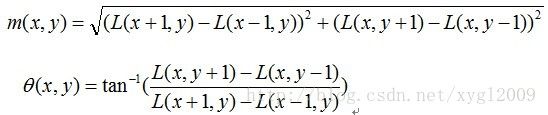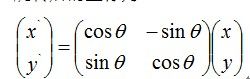图像匹配算法之初探尺度不变特征变换(SIFT)算法

十二月主要看书复习期末考去了，没写博客了。哎。。。中国的研究僧考试还占这么大的比重。不吐槽了。。。。。

这学期主要学习了下SIFT算法，在博客的前面大概对其做了一个概述ubuntu下编译opensift。参考网上几位大神的神作，结合自己查阅的一些资料。现对其进行整理如下：

一、概述

1.     引言

    图像匹配是解决计算机视觉领域诸多问题的一个最基础的方面，比如图像识别、图像拼接、动态追踪等等。图像匹配是指通过一定的匹配算法在两幅或多幅图像之间识别同名点，如二维图像匹配中通过比较目标区和搜索区中相同大小的窗口的相关系数，取搜索区中相关系数最大所对应的窗口中心点作为同名点。其实质是在基元相似性的条件下，运用匹配准则的最佳搜索问题。

     图像匹配大致可以分为基于区域的方法和基于特征的方法。区域的图像配准方法直接计算两幅图像灰度值的相关度确定两者之间的关系，而特征的图像配准方法通过图像的特征判断相似程度。基于像素灰度值的相关算法(例如SSAD，NNPROD等)的缺点是对图像的尺度、旋转、亮暗、视角等变换敏感，计算量大；相比之下，基于局部特征(例如角点、SIFT、SURF等)的算法对图像的一些几何和光度变换具有不变性，计算量较小。本文对图像匹配的研究采用基于局部特征的方法，使用尺度不变特征变换(scale invariant feature transform，SIFT)算法对图像匹配做一研究。

2.   背景

    局部关键点进行图像匹配最早可追溯至1981年，Moravec在立体匹配中使用了角点检测算子。在1988年，Harris和Stephens对其进行了一些改进，Harris又在1992年改进用于动作追踪，自此Harriscorner detector被广泛应用。1997年Schmid和Mohr做出了开拓性的工作，证明局部的不变特征可以应用于图像识别。但Harris corner detector对图像尺度、视角、照明变化比较敏感，抗噪声能力差，所以对不同大小的图像匹配效果不佳。

针对以上的情况，1999年，Lowe,D.G提出了一种具有尺度不变性的特征算子，此算子不仅具有尺度、旋转、视角、光照不变性，而且对目标的运动、遮挡、噪声等因素也保持较好的匹配性。2004年Lowe在其发表的论文《Distinctive Image Features from Scale-Invariant Keypoints》中对此SIFT算法的原理做了详细的叙述，SIFT算子的优点是匹配点多而且稳定，广泛地适用于机器人定位、地图生成以及三维目标识别。

二、SIFT算法原理    

尺度不变特征变换(SIFT)算法，主要提取的是图像中不受外部因素影响的特征点，主要的步骤有以下四步：

⑴尺度空间极值点检测。运算的第一步要搜索所有的尺度及其像素位置。通过使用高斯差分函数，找出对尺度和方向不变的潜在的特征点。

⑵关键点定位。通过第一步所找出来的点不一定是可用的，由于空间是离散化的，极值点的位置精度也被限制于离散点上，所以关键点的选取需要依据它们的稳定性。

⑶关键点方向分配。分配一个或者多个方向给每一个关键点，依照这个方向做进一步的计算， 利用关键点邻域像素的梯度方向分布特性为每个关键点指定方向参数，使算子具备旋转不变性。

⑷关键点描述符。生成SIFT特征向量，将坐标轴旋转到特征点方向，以保证旋转不变性。

    SIFT算法最大的优点是找出的特征点基本上覆盖了图像的每一个区域和位置，例如一幅2.5K像素的图片可以产生大约2000个稳定的特征点。对于图像匹配和识别，SIFT特征子首先从一组相关的图像中提取出来，然后存储到数据库。然后通过与数据库中特征子的比较，找出其中可能的特征点，再依据它们特征向量之间的欧式距离，来实现与新图像的匹配。

三、算法的具体实现

1、检测空间极值点

   关键点的检测使用级联滤波的方法实现，使用高效的算法来找出极值点可能存在的位置，然后再进行进一步的详细的检测。同一物体在不同视角下，它的位置和尺度的信息可以重复地分配，找出这样的特征点是关键点检测的第一步。要找出这些点就要寻找在所有尺度上都具有稳定特性的点，这就需要我们使用尺度空间来达到这种目的。

     尺度空间理论最早出现在计算视觉中是为了模拟图像数据的多尺度特征，“尺度空间”是著名的“图像金字塔”的补充，Koenderink和Lindeberg的研究表明唯一可能的线性尺度核就是高斯函数。图像的尺度空间定义为一个函数，它是由尺度变化的高斯函数和输入图像的卷积形成的，计算公式如下：

                                         

 

      其中以上式中：(x,y)为像素坐标；为尺度空间因子；L为尺度空间。的大小决定了图像的平滑程度，大的尺度对应于图像的概貌特征，小尺度对应图像的细节特征。

高斯尺度空间建立完成后，为了快速高效地检测出尺度空间中的极值点。我们首先要建立差分高斯尺度空间(Difference-of-Gaussian)，在DOG中把每个像素与其周围的26个像素点比较，找出极值。DOG函数是相邻两个图像尺度之差，具体实现如下：

一个点(图中X点)如果在DoG尺度空间本层以及上下两层的26个领域中是极大值或者最小值时，就认为该点是图像在该尺度下的一个特征点，如图一所示。

       

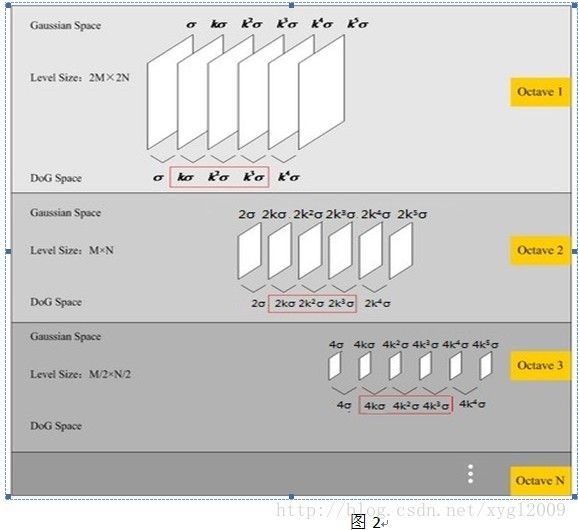
这里要注意的一点是，这个尺度变化因子的取值。现在令Scale=Kⁿ(n=1,2,3…)，Lowe在其论文中提出这里取K=2^1/s，这里的s为高斯金字塔的层数。在极值比较的过程中，每一组图像的首末两层是无法进行极值比较的，为了满足尺度变化的连续性，我们在每一组图像的顶层继续用高斯模糊生成了 3 幅图像，高斯金字塔有每组S+3层图像。DOG金字塔每组有S+2层图像。取s=3的结果，高斯空间及其DoG空间如图2所示。另外，随着Scale的变大，计算量就会增加，为了避免这一点，后面每个octave为上一个octave降采样的结果，即原图的1/4（长宽分别减半），这样就避免了卷积核矩阵的扩大。

2、关键点精确定位

由于DoG算子会产生较强的边缘响应，需要通过拟和三维二次函数以精确确定关键点的位置和尺度，同时去除低对比度的关键点和不稳定的边缘响应点，提高匹配的稳定性以及抗噪声能力。另外对于在三维尺度空间D(x,y,σ)找出来的极值点，由于空间是离散化的，极值点的位置精度被限制在离散点上。我们通过把DoG函数利用泰勒公式进行2次展开来提高精度。展开式如下：

，这里需要注意的是X^T=(x,y,σ)是一个向量。

极值点存在的地方导数应当为零，令，然后得，为精确的位置。

在得到的所有的精确点中，我们需要去掉其中的低对比度的特征点，所进行的操作如下：则舍弃这个点，否则就保留。

   下面讨论排除不稳定的边缘点。高斯差分在图像边缘处会有比较大的值，但并非所有的边缘点都可以作为稳定的好的特征关键点。我们需要排除在穿过边缘的方向上变化较大，而在相垂直的方向上变化很小，这个变化的大小我们通过主曲率来衡量。查资料得知，不好的高斯差分算子(DoG)的极值在横跨边缘的地方有较大的主曲率，而在垂直边缘的方向有较小的主曲率。而主曲率通过一个2×2 的Hessian矩阵H求出。其中Hessian矩阵，如下所示：

                   

通过Hessian矩阵的性质可知，矩阵的两个特征值分别表征了两个D在两个相垂直方向上的变化率。设α为幅值较大的特征值，β为幅值较小的特征值。取r为两个特征值之比，α=r*β，则有如下结果：

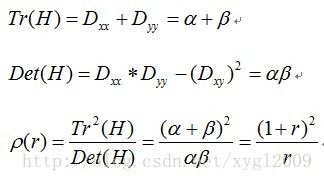
容易看出随着r的增大而增大，因此为了检测曲率是否在某阀值下，只需检测在某个给定的下，判定是否成立，如果成立接受这个点，不成立则去除这个点。

3、关键点方向的分配

利用关键点领域像素的梯度方向分布特性，为每个关键点指定方向参数，使算子具备旋转不变性。梯度方向是很容易想到的，仅仅取特征点上的梯度方向，会不太稳定。为此采用关键点周围一块区域内的梯度信息综合，作为关键点的方向。方向计算是在图像尺度空间L(x,y,σ)上进行的，且尺度与关键点所在尺度相同。二维空间上每一点的梯度（包括幅值m(x,y)和角度θ(x,y)）可以用以下方程表示:

   在以这个特征点为中心的领域窗口内采样，采用直方图统计领域像素的梯度方向。梯度直方图的范围是0~360°，我们采取每10°一个柱，一共有36个柱。随着距离中心点越远，对于直方图的响应越小。为了得到比较平滑的直方图，可以采用高斯函数对直方图进行平滑滤波，减少突变的状况。统计结束后，直方图的峰值则代表了该关键点处邻域梯度的主方向，即作为该关键点的方向，其他的达到最大值80%的方向可作为辅助方向，如图3所示。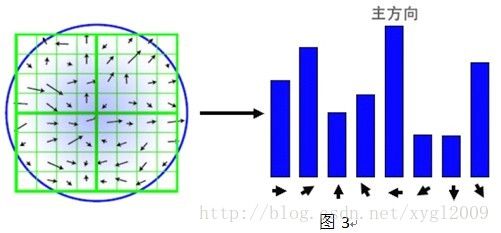

4、局部图像描述符的生成

通过前面三步，关键点的位置、尺度和方向。如果想要匹配，我们可以直接将两幅图像关键点附近的区域进行相关性分析计算，根据相似度来判断是否匹配。这样做有两个问题，一个是计算量太大，另一个是这种方法对于仿射变换很敏感，因为仿射变换后图像由于扭曲，相关性已经降低了。对于第一个问题，我们可以折中只取几个参数来描述这个小区域，只比较这几个参数的差别；对于第二个问题，以关键点附近的多个点为中心分别计算梯度方向分布直方图，不同角度投影的图像即使在精确关键点位置处不能很好地匹配，但是有可能在关键点附近点上得到较好的匹配，这样也增加了描述参数的数量，减少了误匹配的可能。

首先为了保证特征矢量具有旋转不变性，要以特征点为中心，在附近邻域内旋转θ角，即旋转为特征点的方向，如图4所示。

变换后坐标：

将旋转后区域划分为4×4个子区域，在子区域内计算8个方向的梯度直方图，绘制每个方向梯度方向的累加值，形成一个种子点。与求主方向不同的是，此时，每个子区域梯度方向直方图将0°~360°划分为8个方向区间，每个区间为45°。即每个种子点有8个方向区间的梯度强度信息。如图5所示，图左部分的中央为当前关键点的位置，每个小格代表关键点邻域所在尺度空间的一个像素，利用公式求得每个像素的梯度幅值与梯度方向，箭头方向代表该像素的梯度方向，箭头长度代表梯度模值，然后用高斯窗口对其进行加权运算。

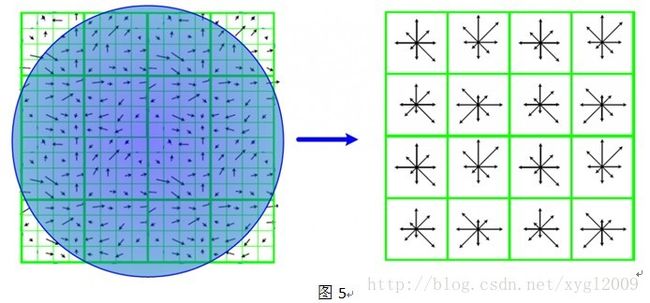
5、根据SIFT特征进行图像匹配

两幅图像的SIFT特征向量生成后，下一步采用关键点特征向量的欧式距离来作为两幅图像中关键点的相似性判定度量。取第一幅图像中的某个关键点，并找出其与第二幅图像中欧式距离最近的前两个关键点，在这两个关键点中，如果最近的距离除以次近的距离小于某个比例阈值，则接受这一对匹配点。降低这个比例阈值，SIFT匹配点数目会减少，但更加稳定。为了排除因为图像遮挡和背景混乱而产生的无匹配关系的关键点，比较最近邻距离与次近邻距离称为距离比率(ratio)小于某个阈值的认为是正确匹配。因为对于错误匹配,由于特征空间的高维性,相似的距离可能有大量其他的错误匹配,从而它的ratio值比较高，通常ratio=0.8。ratio的取值原则如下:

ratio=0. 4　对于准确度要求高的匹配；

ratio=0. 6　对于匹配点数目要求比较多的匹配； 

ratio=0. 5　一般情况。

也可按如下原则:当最近邻距离<200时ratio=0. 6，反之ratio=0. 4。ratio的取值策略能排分错误匹配点。

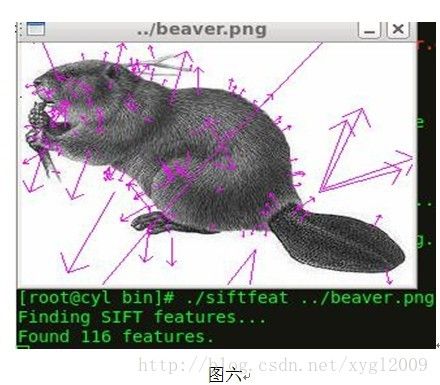
本文采用Rob Hess在Github上维护的开源Opensift的C代码进行对匹配的测试。测试效果如下图六、图七所示。其中图六表示找出图像中的SIFT特征点，一共有116个。图七表示匹配的结果。

    

四、总结

      本文对SIFT算法以及简单的应用做了一个简要的分析，这些分析还远远不够，充其量只能算作是初窥算法的魅力，后续仍然需要做大量的工作，进一步对图像匹配相关算法做深入的研究。

SIFT及其扩展算法已被证实在同类描述算子中具有最强的鲁棒性。其主要特点表现在：1)独特性(Distinctiveness)好，信息量丰富，适用于在海量特征数据库中进行快速、准确的匹配。2)多量性，即使少数的几个物体也可以产生大量SIFT特征向量。3)高速性，经优化的SIFT匹配算法甚至可以达到实时的要求。4)可扩展性，可以很方便的与其他形式的特征向量进行联合。

SIFT算法仍然存在一些不足。首先，是实时性不高；其次，是关键点主要依附于边缘拐角，因此对于边缘模糊和边缘光滑的图像，提取出的关键点就很少；最后，SIFT是在灰度图像上进行，不能充分利用图像的彩色信息。

    2006年，Herbert Bay等人提出的SURF(SpeededUp Robust Feature)算法, 同SIFT算法相同SURF算法，通过对LoG(Laplacian of Gaussian),即高斯拉普拉斯算子的归一化近似来选取图像中的特征点,然后通过DoH (Determinant of Hessian)简化了SIFT算法中对特征点的描述。

SURF算法的提出是针对1999 年D.G.Lowe等人提出的SIFT算法数据量大,时间复杂度高,时效性差的问题。它继承了SIFT算法抗干扰能力强、区分度高等诸多优点,同时在计算速度上提高了数倍，适合在嵌入式设备上进行应用，极大地扩展局部特征匹配算法的应用范围。