[Unity基础]游戏中的数学
一、坐标系
1.世界坐标系:使用左手坐标系,即z轴方向跟人眼向前看的方向一致(右手坐标系z轴方向跟人眼向前看的方向相反)
2.本地坐标系
3.屏幕坐标系:左下为原点,右上为屏幕宽高
4.界面坐标系:左上为原点,右下为屏幕宽高(unity自带的gui使用的就是这个)
5.视口坐标系:Camera组件的Viewport Rect
6.齐次坐标系:用(x,y,z,w)来区分点和向量。例如(1,2,3,0),w为0时表示向量,为1时表示点
二、向量
1.点乘:主要用于计算两向量间的夹角,或者判断角度范围。向量a(a1,a2,a3)点乘向量b(b1,b2,b3)等于|a|*|b|*cos<a,b>,或等于a1xb1+a2xb2+a3xb3
Mathf.Asin/Mathf.Acos/Mathf.Atan:返回一个以弧度为计算单位的值
Mathf.Rad2Deg:弧度转度,相当于360/(PI * 2)
可以通过Mathf.Acos(点乘结果)*Mathf.Rad2Deg得出两向量的夹角,不过更方便的方法是:Vector3.Angle
2.叉乘:得到一个垂直于两个向量的向量。|向量a点乘向量b|等于|a|*|b|*sin<a,b>
三、矩阵
主要用于shader中的顶点片段着色器。游戏中的移动、旋转和缩放实际上是向量与矩阵运算的结果。
定义:矩阵主要用来描述两个坐标系统间的关系,通过定义一种运算而将一个坐标系中的向量转换到另一个坐标系中。
维度:指包含了多少行和多少列。一个r x c矩阵有r行、c列。
方阵:行数和列数相同的矩阵称为方阵。方阵的对角线元素就是方阵中行号和列号相同的元素,其余为非对角线元素。如果所有非对角线元素都为0,则称这种矩阵为对角矩阵。例如:
单位矩阵:是一种特殊的对角矩阵,n维单位矩阵记作I n,是n x n矩阵,对角线元素是1,其他元素是0。例如,3 x 3单位矩阵:
向量作为矩阵使用:一个n维向量能被当作1 x n矩阵或n x 1矩阵,1 x n矩阵称作行向量,n x 1矩阵称作列向量。行向量平着写,列向量竖着写,例如:
转置:考虑一个r x c矩阵M,M的转置记作M T,是一个c x r矩阵,例如:
标量和矩阵的乘法:
矩阵和矩阵的乘法:一个r x n的矩阵A乘以一个n x c的矩阵B,结果是一个r x c矩阵,记作C。对于C中的任意元素,取A的第i行和B的第j列,将行和列中的对应元素相乘,然后将结果相加(等于A的第i行和B的第j列的点积):
向量与矩阵的乘法:因为向量能被当作一行或一列的矩阵,因此同上。向量乘以一个矩阵,相当于执行了一次坐标转换:
上面表示将向量(x, y, z)转换到以p、q、r为坐标轴的坐标系中。
四、四元数
与旋转相关的数。一般情况下可以由欧拉角代替,但欧拉角会产生万向锁问题,所以旋转最好使用四元数。
![[Unity基础]游戏中的数学_第1张图片](http://img.e-com-net.com/image/info5/f046a56ca7ab439c9837cb703e06d9d6.jpg)
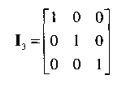

![[Unity基础]游戏中的数学_第2张图片](http://img.e-com-net.com/image/info5/53810d0c2b66497c928a4771b168397e.jpg)
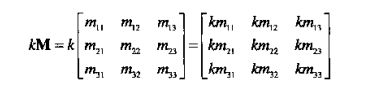
![[Unity基础]游戏中的数学_第3张图片](http://img.e-com-net.com/image/info5/90bed9766f4148a1b062868e24d1cb3d.jpg)
![[Unity基础]游戏中的数学_第4张图片](http://img.e-com-net.com/image/info5/716aed23e7dd41eea4d6076bfc2abd7e.jpg)
![[Unity基础]游戏中的数学_第5张图片](http://img.e-com-net.com/image/info5/9d8cba9b0b72417b9a0ff5f4b87b9052.jpg)