sift尺度空间的理解以及计算

为了保持尺度不变的特性，作者构建高斯金字塔及差分金字塔的方法来取得极值点。

 

但是其中的尺度的计算有点不太理解，看了源码和网络上的分析后做个笔记

 

class CV_EXPORTS_W SIFT : public Feature2D
{
public:
    CV_WRAP explicit SIFT( int nfeatures=0, int nOctaveLayers=3,
          double contrastThreshold=0.04, double edgeThreshold=10,
          double sigma=1.6);

下面的一段代码是opencv中关于sift的构造函数的代码

可以看到，把组中层数初始化为3，（作者建议3-5），边缘阈值10，去除边缘相应的点，sigma0为1.6，高斯模糊的尺度，这是最模糊的尺度。

然后构建高斯金字塔。

其中组数由下式计算得出

int nOctaves = actualNOctaves > 0 ? actualNOctaves : cvRound(log( (double)std::min( base.cols, base.rows ) ) / log(2.) - 2) - firstOctave;

这个也很好理解，在多分辨率的组采样中，每次按行缩小两倍，列缩小两倍，即像素个数减少为1/4。

sig[0] = sigma; sigma就是一开始赋予的初值

 

当前层为上层的k倍，即同一组之间的不同层之间的关系。

 

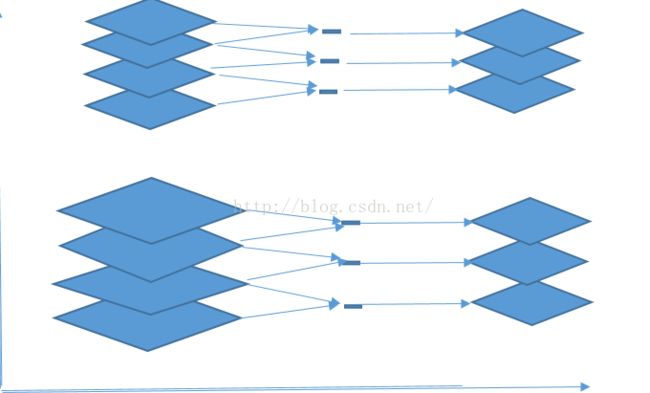
那有代码可以看出，上面的一组的第一副图像是下面一组的倒数第三层的图像的降采样得到。

关于层数= nOctaveLayers + 3的原因有几个

1. 为了保持尺度的连续性

2. 为了构建S+2层的差分金字塔，其实跟上面差不多

3. 为了计算极值的时候S层都可以得到计算

 

那么组与组之间的尺度连续性体现在哪？

void SIFT::buildGaussianPyramid( const Mat& base, vector<Mat>& pyr, int nOctaves ) const
{
    vector<double> sig(nOctaveLayers + 3);
    pyr.resize(nOctaves*(nOctaveLayers + 3));

    // precompute Gaussian sigmas using the following formula:
    //  \sigma_{total}^2 = \sigma_{i}^2 + \sigma_{i-1}^2
    sig[0] = sigma;
    double k = pow( 2., 1. / nOctaveLayers );
    for( int i = 1; i < nOctaveLayers + 3; i++ )
    {
        double sig_prev = pow(k, (double)(i-1))*sigma;
        double sig_total = sig_prev*k;
        sig[i] = std::sqrt(sig_total*sig_total - sig_prev*sig_prev);
    }
….
….
…
}