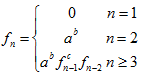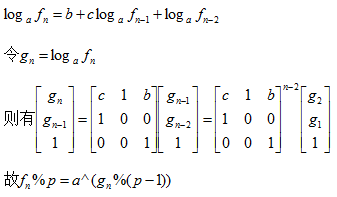- leetcode-124 Binary Tree Maximum Path Sum
乐观的大鹏
LeetCode
Givenanon-emptybinarytree,findthemaximumpathsum.Forthisproblem,apathisdefinedasanysequenceofnodesfromsomestartingnodetoanynodeinthetreealongtheparent-childconnections.Thepathmustcontainatleastonenodea
- LeetCode 673. Number of Longest Increasing Subsequence (Java版; Meidum)
littlehaes
字符串动态规划算法leetcode数据结构
welcometomyblogLeetCode673.NumberofLongestIncreasingSubsequence(Java版;Meidum)题目描述Givenanunsortedarrayofintegers,findthenumberoflongestincreasingsubsequence.Example1:Input:[1,3,5,4,7]Output:2Explanatio
- 致良知之寄诸用明书
BonSun
众所周知,当今社会,父母和社会、学校对学生的期望往往是唯分数论,包括每个人对成功的理解也往往是功名利禄,忽视了最基本的学问。文中提到,花之千叶者无实,为其华美太发露耳。人只有沉下心来,韬光养晦,才能拥有真正的学问和本领。
- Biopython提取和分离复合体PDB文件中所有链的结构信息
qq_27390023
生物信息学python
从蛋白质复合体的PDB文件中提取每个链的结构信息,并保存成单独的pdb文件。示例代码fromBioimportPDBdefextract_chain_sequences(pdb_file,output_dir):"""从PDB文件中提取所有链的序列,并保存为独立的PDB文件。:parampdb_file:蛋白质复合体PDB文件路径:paramoutput_dir:输出目录,用于保存各链的PDB文件
- 详解TCP的三次握手
汪先声
tcp/ip网络协议网络
TCP(三次握手)是指在建立一个可靠的传输控制协议(TCP)连接时,客户端和服务器之间的三步交互过程。这个过程的主要目的是确保连接是可靠的、双方的发送与接收能力是正常的,并且可以开始数据传输。下面是对每个步骤的详细解释:1.第一次握手:客户端发送SYN过程:客户端(A)向服务器(B)发送一个同步报文段(SYN,SynchronizeSequenceNumber),表示它想要与服务器建立连接。目的:
- LeetCode 2207. 字符串中最多数目的子字符串
Sasakihaise_
LeetCodeleetcode后缀和
题目链接:力扣https://leetcode-cn.com/problems/maximize-number-of-subsequences-in-a-string/【分析】由于pattern中只有两个字符,假设分别是a、b,只需要统计出text中每个a后面有多少b即可,这儿这个通过后缀和的思想,先算出总的b的个数,如果当前字符是a,那么后面b的个数就是总的b的个数,如果是b,就把总的b的个数-
- Python【math数学函数】
Alan_Lowe
#Pythonpython
Python【math数学函数】文章目录Python【math数学函数】数论与表示函数1.ceil()和floor()2.comb()3.copysign()4.fabs()5.factorial()6.gcd()7.lcm()幂函数与对数函数1.exp()和math.e和pow()2.log()和log2()和log10()3.sqrt(x)三角函数1.asin、acos()、atan()2.s
- python 实现eulers totient欧拉方程算法
luthane
算法python开发语言
eulerstotient欧拉方程算法介绍欧拉函数(Euler’sTotientFunction),通常表示为(),是一个与正整数相关的函数,它表示小于或等于的正整数中与互质的数的数目。欧拉函数在数论和密码学中有广泛的应用。欧拉函数的性质1.**对于质数,有φ(p)=p−1∗∗φ(p)=p−1^{**}φ(p)=p−1∗∗。2.**如果是质数的次幂,即n=pkn=p^kn=pk,则φ(n)=pk−
- 自学Python:计算斐波纳契数列
小强聊成长
斐波那契数列(Fibonaccisequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(LeonardodaFibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N*)在现代物理、准
- 一维数组 list 呢 ,怎么转换成 (批次 句子长度 特征值 )三维向量 python pytorch lstm 编程 人工智能
zhangfeng1133
pythonpytorch人工智能数据挖掘
一、介绍对于一维数组,如果你想将其转换成适合深度学习模型(如LSTM)输入的格式,你需要考虑将其扩展为三维张量。这通常涉及到批次大小(batchsize)、序列长度(sequencelength)和特征数量(numberoffeatures)的维度。以下是如何将一维数组转换为这种格式的步骤:###1.确定维度-**批次大小(BatchSize)**:这是你一次处理的样本数量。-**序列长度(Seq
- HDU - 1398 完全背包问题求方案数
tran_sient
算法以及模板完全背包求方案数
题目描述:ProblemDescriptionPeopleinSilverlandusesquarecoins.Notonlytheyhavesquareshapesbutalsotheirvaluesaresquarenumbers.Coinswithvaluesofallsquarenumbersupto289(=17^2),i.e.,1-creditcoins,4-creditcoins,9
- 顺序表(SequenceList)数据结构的基本操作实现详解
SuchABigBug
C语言数据结构链表c语言
目录一、前言二、整体设计框架三、函数实现1.SeqListInit2.SeqListDestory3.SeqListCheckCapacity4.SeqListPushBack(尾插)5.SeqListPopBack(尾删)6.SeqListPushFront(头插)7.SeqListPopFront(头删)8.SeqlistFind9.SeqListInsert(任意位置插入)9.SeqList
- 动态规划算法之最长公子序列详细解读(附带Java代码解读)
南城花随雪。
算法分析算法动态规划java
最长公共子序列(LongestCommonSubsequence,LCS)问题是动态规划中另一个经典问题,广泛用于比较两个序列的相似度。它的目标是找到两个序列之间最长的公共子序列(不是连续的),使得这个子序列同时出现在两个序列中。1.问题定义给定两个序列X和Y,要找到它们的最长公共子序列,即一个序列Z,它同时是X和Y的子序列,且Z的长度最大。例如:对于序列X="ABCBDAB"和Y="BDCAB"
- HDU 1573X问题(扩展中国剩余定理)
数学收藏家
数据结构算法
ProblemDescription求在小于等于N的正整数中有多少个X满足:Xmoda[0]=b[0],Xmoda[1]=b[1],Xmoda[2]=b[2],…,Xmoda[i]=b[i],…(0usingnamespacestd;#defineintlonglong#defineendl'\n'#defineIOSios::sync_with_stdio(false);cin.tie(0);c
- LeetCode题解:Word Ladder
CheeRok
LeetCodeLeetCode全题解leetcode
Giventwowords(beginWordandendWord),andadictionary’swordlist,findthelengthofshortesttransformationsequencefrombeginWordtoendWord,suchthat:OnlyonelettercanbechangedatatimeEachintermediatewordmustexistin
- C语言 | Leetcode C语言题解之第392题判断子序列
DdddJMs__135
分享C语言Leetcode题解
题目:题解:boolisSubsequence(char*s,char*t){intn=strlen(s),m=strlen(t);intf[m+1][26];memset(f,0,sizeof(f));for(inti=0;i=0;i--){for(intj=0;j<26;j++){if(t[i]==j+'a')f[i][j]=i;elsef[i][j]=f[i+1][j];}}intadd=0
- 代码随想录算法训练营Day22 | 491.递增子序列,46.全排列,47.全排列 II ,332. 重新安排行程,51. N皇后,37. 解数独,总结
Yummy Penguin
算法
第七章回溯算法part04491.递增子序列本题和大家刚做过的90.子集II非常像,但又很不一样,很容易掉坑里。代码随想录视频讲解:回溯算法精讲,树层去重与树枝去重|LeetCode:491.递增子序列_哔哩哔哩_bilibili#491classSolution:deffindSubsequences(self,nums):result=[]path=[]self.backtracking(nu
- HDU2196Computer 树形dp
Vibrant
传送门解法1树的直径参考博客#include//树的直径#defineMAXN10010usingnamespacestd;typedefpairP;intdis[MAXN],Max,root;vectora[MAXN];voidInit(intn){Max=0;for(inti=1;iMax)Max=sum,root=now;for(inti=0;i//记忆化搜索#defineMAXN10010
- C++ | Leetcode C++题解之第392题判断子序列
Ddddddd_158
经验分享C++Leetcode题解
题目:题解:classSolution{public:boolisSubsequence(strings,stringt){intn=s.size(),m=t.size();vector>f(m+1,vector(26,0));for(inti=0;i=0;i--){for(intj=0;j<26;j++){if(t[i]==j+'a')f[i][j]=i;elsef[i][j]=f[i+1][j
- python安全渗透笔记
红云谈安全
python编程学习python安全
Python学习python常见错误UnicodeDecodeError:‘gbk’codeccan’tdecodebyte0x8cinposition22:illegalmultibytesequence//打开的文件未编码encoding='UTF-8'expectedanindentedblock未缩进,ifforcontinue又进入一次新的循环%将其他变量置入字符串特定位置以生成新字符串
- 胶水105
假装是老付
捕捉这些脱节的最好方法是按顺序给我自己讲一个故事,并考虑到我从以前的那些对话中收集到【工作任务之间】的那些依赖关系。Thebestwaytocatchthesedisconnectsistotellmyselfastoryinasequence,consideringdependenciesI’vegleanedfrompreviousconversations.例二EXAMPLE2来自销售团队的
- Kafka高性能揭秘 —— sequence IO、PageCache、SendFile的应用详解
大数据学习与分享
Kafkakafka大数据java
大家都知道Kafka是将数据存储于磁盘的,而磁盘读写性能往往很差,但Kafka官方测试其数据读写速率能达到600M/s,那么为什么Kafka性能会这么高呢?首先producer往broker发送消息时,采用batch的方式即批量而非一条一条的发送,这种方式可以有效降低网络IO的请求次数,提升性能。此外这些批次消息会"暂存"在缓冲池中,避免频繁的GC问题。批量发送的消息可以进行压缩并且传输的时候可以
- vLLM (3) - Sequence & SequenceGroup
戴昊光
人工智能languagemodelnlppythontransformer
系列文章目录vLLM(1)-Qwen2推理&部署vLLM(2)-架构总览vLLM(3)-Sequence&SequenceGroup文章目录系列文章目录前言一、SequenceStage&SequenceStatus1.SeqenceStage2.SeqenceStatus二、SequenceData&Sequence1.SequenceData2.Sequence三、SequenceGroup&
- 创建sequence sql模板
wrx繁星点点
#新增模板sql数据库
createsequenceSEQ_CLE_FUND_ADJU_APPLY(序列名)minvalue(最小值)1nomaxvalue(如果间隔值>0说明是递增序列可以不需要最大值就使用nomaxvalue代替maxvalue9999999999,如果间隔值<0说明是递减序列可以不需要最小值就可以使用nominvalue)startwith(起始值:默认为1)1incrementby(间隔数:每次加
- 算法设计与分析学习(6)——数论
罗塞菈桔梨萝柚
算法学习算法线性代数
数论整除基本概念若aaa和bbb为整数,且a≠0a≠0a=0若存在整数qqq使得b=aqb=aqb=aq,那么就说aaa可以整除bbb或是bbb被aaa整除,记作a∣ba|ba∣b。aaa也被称为bbb的约数,bbb也被称为a的倍数。若bbb不能被aaa整除,则记作a∤ba\not{|}ba∣b。整数p≠0,±1p≠0,±1p=0,±1,且除了±1,±p±1,±p±1,±p外没有其他的约数
- 浙大数据结构:01-复杂度2 Maximum Subsequence Sum
_Power_Y
数据结构浙大数据结构c++
数据结构MOOCPTA习题01-复杂度2MaximumSubsequenceSum#includeusingnamespacestd;constintM=100005;inta[M];intmain(){intk;cin>>k;intf=1;for(inti=0;i>a[i];if(a[i]>=0)//如果出现大于0则进行在线处理f=0;}if(f){//全都小于0coutma){//更新答案ma
- hive序列生成_Hive实现自增列的两种方法
weixin_39559804
hive序列生成
多维数据仓库中的维度表和事实表一般都需要有一个代理键,作为这些表的主键,代理键一般由单列的自增数字序列构成。Hive没有关系数据库中的自增列,但它也有一些对自增序列的支持,通常有两种方法生成代理键:使用row_number()窗口函数或者使用一个名为UDFRowSequence的用户自定义函数(UDF)。用row_number()函数生成代理键INSERTOVERWRITETABLEmy_hive
- 2020-08-13 To Succeed in The Long-Term, Think in 5, 10, or 20 Year Time Frames
春生阁
Humanscanbeprettygoodatshort-termthinking—butwe’renotverygoodatthinkingaboutthelong-termconsequencesofourpresentactions.Thepressuresofmodernlifemakeitincrediblydifficultforustoprojecttheimplicationsof
- AtCoder Beginner Contest 369(ABCDEFG题)视频讲解
阿史大杯茶
Atcoderc++算法数据结构
A-369ProblemStatementYouaregiventwointegersAAAandBBB.Howmanyintegersxxxsatisfythefollowingcondition?Condition:ItispossibletoarrangethethreeintegersAAA,BBB,andxxxinsomeordertoformanarithmeticsequence.A
- 数论——欧几里得算法
NarutoTime
数论算法c++数据结构c语言
1.欧几里得简介 欧几里得(希腊文:Ευκλειδης,约公元前330年—公元前275年),古希腊数学家,被称为“几何之父”。他最著名的著作《几何原本》是欧洲数学的基础,在书中他提出五大公设。欧几里得的《几何原本》被广泛的认为是历史上最成功的教科书。欧几里得也写了一些关于透视、圆锥曲线、球面几何学及数论的作品。2.欧几里得算法欧几里得算法用于:求解a和b的最大公约数。最大公约数英文为:Gre
- Spring的注解积累
yijiesuifeng
spring注解
用注解来向Spring容器注册Bean。
需要在applicationContext.xml中注册:
<context:component-scan base-package=”pagkage1[,pagkage2,…,pagkageN]”/>。
如:在base-package指明一个包
<context:component-sc
- 传感器
百合不是茶
android传感器
android传感器的作用主要就是来获取数据,根据得到的数据来触发某种事件
下面就以重力传感器为例;
1,在onCreate中获得传感器服务
private SensorManager sm;// 获得系统的服务
private Sensor sensor;// 创建传感器实例
@Override
protected void
- [光磁与探测]金吕玉衣的意义
comsci
这是一个古代人的秘密:现在告诉大家
信不信由你们:
穿上金律玉衣的人,如果处于灵魂出窍的状态,可以飞到宇宙中去看星星
这就是为什么古代
- 精简的反序打印某个数
沐刃青蛟
打印
以前看到一些让求反序打印某个数的程序。
比如:输入123,输出321。
记得以前是告诉你是几位数的,当时就抓耳挠腮,完全没有思路。
似乎最后是用到%和/方法解决的。
而今突然想到一个简短的方法,就可以实现任意位数的反序打印(但是如果是首位数或者尾位数为0时就没有打印出来了)
代码如下:
long num, num1=0;
- PHP:6种方法获取文件的扩展名
IT独行者
PHP扩展名
PHP:6种方法获取文件的扩展名
1、字符串查找和截取的方法
1
$extension
=
substr
(
strrchr
(
$file
,
'.'
), 1);
2、字符串查找和截取的方法二
1
$extension
=
substr
- 面试111
文强chu
面试
1事务隔离级别有那些 ,事务特性是什么(问到一次)
2 spring aop 如何管理事务的,如何实现的。动态代理如何实现,jdk怎么实现动态代理的,ioc是怎么实现的,spring是单例还是多例,有那些初始化bean的方式,各有什么区别(经常问)
3 struts默认提供了那些拦截器 (一次)
4 过滤器和拦截器的区别 (频率也挺高)
5 final,finally final
- XML的四种解析方式
小桔子
domjdomdom4jsax
在平时工作中,难免会遇到把 XML 作为数据存储格式。面对目前种类繁多的解决方案,哪个最适合我们呢?在这篇文章中,我对这四种主流方案做一个不完全评测,仅仅针对遍历 XML 这块来测试,因为遍历 XML 是工作中使用最多的(至少我认为)。 预 备 测试环境: AMD 毒龙1.4G OC 1.5G、256M DDR333、Windows2000 Server
- wordpress中常见的操作
aichenglong
中文注册wordpress移除菜单
1 wordpress中使用中文名注册解决办法
1)使用插件
2)修改wp源代码
进入到wp-include/formatting.php文件中找到
function sanitize_user( $username, $strict = false
- 小飞飞学管理-1
alafqq
管理
项目管理的下午题,其实就在提出问题(挑刺),分析问题,解决问题。
今天我随意看下10年上半年的第一题。主要就是项目经理的提拨和培养。
结合我自己经历写下心得
对于公司选拔和培养项目经理的制度有什么毛病呢?
1,公司考察,选拔项目经理,只关注技术能力,而很少或没有关注管理方面的经验,能力。
2,公司对项目经理缺乏必要的项目管理知识和技能方面的培训。
3,公司对项目经理的工作缺乏进行指
- IO输入输出部分探讨
百合不是茶
IO
//文件处理 在处理文件输入输出时要引入java.IO这个包;
/*
1,运用File类对文件目录和属性进行操作
2,理解流,理解输入输出流的概念
3,使用字节/符流对文件进行读/写操作
4,了解标准的I/O
5,了解对象序列化
*/
//1,运用File类对文件目录和属性进行操作
//在工程中线创建一个text.txt
- getElementById的用法
bijian1013
element
getElementById是通过Id来设置/返回HTML标签的属性及调用其事件与方法。用这个方法基本上可以控制页面所有标签,条件很简单,就是给每个标签分配一个ID号。
返回具有指定ID属性值的第一个对象的一个引用。
语法:
&n
- 励志经典语录
bijian1013
励志人生
经典语录1:
哈佛有一个著名的理论:人的差别在于业余时间,而一个人的命运决定于晚上8点到10点之间。每晚抽出2个小时的时间用来阅读、进修、思考或参加有意的演讲、讨论,你会发现,你的人生正在发生改变,坚持数年之后,成功会向你招手。不要每天抱着QQ/MSN/游戏/电影/肥皂剧……奋斗到12点都舍不得休息,看就看一些励志的影视或者文章,不要当作消遣;学会思考人生,学会感悟人生
- [MongoDB学习笔记三]MongoDB分片
bit1129
mongodb
MongoDB的副本集(Replica Set)一方面解决了数据的备份和数据的可靠性问题,另一方面也提升了数据的读写性能。MongoDB分片(Sharding)则解决了数据的扩容问题,MongoDB作为云计算时代的分布式数据库,大容量数据存储,高效并发的数据存取,自动容错等是MongoDB的关键指标。
本篇介绍MongoDB的切片(Sharding)
1.何时需要分片
&nbs
- 【Spark八十三】BlockManager在Spark中的使用场景
bit1129
manager
1. Broadcast变量的存储,在HttpBroadcast类中可以知道
2. RDD通过CacheManager存储RDD中的数据,CacheManager也是通过BlockManager进行存储的
3. ShuffleMapTask得到的结果数据,是通过FileShuffleBlockManager进行管理的,而FileShuffleBlockManager最终也是使用BlockMan
- yum方式部署zabbix
ronin47
yum方式部署zabbix
安装网络yum库#rpm -ivh http://repo.zabbix.com/zabbix/2.4/rhel/6/x86_64/zabbix-release-2.4-1.el6.noarch.rpm 通过yum装mysql和zabbix调用的插件还有agent代理#yum install zabbix-server-mysql zabbix-web-mysql mysql-
- Hibernate4和MySQL5.5自动创建表失败问题解决方法
byalias
J2EEHibernate4
今天初学Hibernate4,了解了使用Hibernate的过程。大体分为4个步骤:
①创建hibernate.cfg.xml文件
②创建持久化对象
③创建*.hbm.xml映射文件
④编写hibernate相应代码
在第四步中,进行了单元测试,测试预期结果是hibernate自动帮助在数据库中创建数据表,结果JUnit单元测试没有问题,在控制台打印了创建数据表的SQL语句,但在数据库中
- Netty源码学习-FrameDecoder
bylijinnan
javanetty
Netty 3.x的user guide里FrameDecoder的例子,有几个疑问:
1.文档说:FrameDecoder calls decode method with an internally maintained cumulative buffer whenever new data is received.
为什么每次有新数据到达时,都会调用decode方法?
2.Dec
- SQL行列转换方法
chicony
行列转换
create table tb(终端名称 varchar(10) , CEI分值 varchar(10) , 终端数量 int)
insert into tb values('三星' , '0-5' , 74)
insert into tb values('三星' , '10-15' , 83)
insert into tb values('苹果' , '0-5' , 93)
- 中文编码测试
ctrain
编码
循环打印转换编码
String[] codes = {
"iso-8859-1",
"utf-8",
"gbk",
"unicode"
};
for (int i = 0; i < codes.length; i++) {
for (int j
- hive 客户端查询报堆内存溢出解决方法
daizj
hive堆内存溢出
hive> select * from t_test where ds=20150323 limit 2;
OK
Exception in thread "main" java.lang.OutOfMemoryError: Java heap space
问题原因: hive堆内存默认为256M
这个问题的解决方法为:
修改/us
- 人有多大懒,才有多大闲 (评论『卓有成效的程序员』)
dcj3sjt126com
程序员
卓有成效的程序员给我的震撼很大,程序员作为特殊的群体,有的人可以这么懒, 懒到事情都交给机器去做 ,而有的人又可以那么勤奋,每天都孜孜不倦得做着重复单调的工作。
在看这本书之前,我属于勤奋的人,而看完这本书以后,我要努力变成懒惰的人。
不要在去庞大的开始菜单里面一项一项搜索自己的应用程序,也不要在自己的桌面上放置眼花缭乱的快捷图标
- Eclipse简单有用的配置
dcj3sjt126com
eclipse
1、显示行号 Window -- Prefences -- General -- Editors -- Text Editors -- show line numbers
2、代码提示字符 Window ->Perferences,并依次展开 Java -> Editor -> Content Assist,最下面一栏 auto-Activation
- 在tomcat上面安装solr4.8.0全过程
eksliang
Solrsolr4.0后的版本安装solr4.8.0安装
转载请出自出处:
http://eksliang.iteye.com/blog/2096478
首先solr是一个基于java的web的应用,所以安装solr之前必须先安装JDK和tomcat,我这里就先省略安装tomcat和jdk了
第一步:当然是下载去官网上下载最新的solr版本,下载地址
- Android APP通用型拒绝服务、漏洞分析报告
gg163
漏洞androidAPP分析
点评:记得曾经有段时间很多SRC平台被刷了大量APP本地拒绝服务漏洞,移动安全团队爱内测(ineice.com)发现了一个安卓客户端的通用型拒绝服务漏洞,来看看他们的详细分析吧。
0xr0ot和Xbalien交流所有可能导致应用拒绝服务的异常类型时,发现了一处通用的本地拒绝服务漏洞。该通用型本地拒绝服务可以造成大面积的app拒绝服务。
针对序列化对象而出现的拒绝服务主要
- HoverTree项目已经实现分层
hvt
编程.netWebC#ASP.ENT
HoverTree项目已经初步实现分层,源代码已经上传到 http://hovertree.codeplex.com请到SOURCE CODE查看。在本地用SQL Server 2008 数据库测试成功。数据库和表请参考:http://keleyi.com/a/bjae/ue6stb42.htmHoverTree是一个ASP.NET 开源项目,希望对你学习ASP.NET或者C#语言有帮助,如果你对
- Google Maps API v3: Remove Markers 移除标记
天梯梦
google maps api
Simply do the following:
I. Declare a global variable:
var markersArray = [];
II. Define a function:
function clearOverlays() {
for (var i = 0; i < markersArray.length; i++ )
- jQuery选择器总结
lq38366
jquery选择器
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
- 基础数据结构和算法六:Quick sort
sunwinner
AlgorithmQuicksort
Quick sort is probably used more widely than any other. It is popular because it is not difficult to implement, works well for a variety of different kinds of input data, and is substantially faster t
- 如何让Flash不遮挡HTML div元素的技巧_HTML/Xhtml_网页制作
刘星宇
htmlWeb
今天在写一个flash广告代码的时候,因为flash自带的链接,容易被当成弹出广告,所以做了一个div层放到flash上面,这样链接都是a触发的不会被拦截,但发现flash一直处于div层上面,原来flash需要加个参数才可以。
让flash置于DIV层之下的方法,让flash不挡住飘浮层或下拉菜单,让Flash不档住浮动对象或层的关键参数:wmode=opaque。
方法如下:
- Mybatis实用Mapper SQL汇总示例
wdmcygah
sqlmysqlmybatis实用
Mybatis作为一个非常好用的持久层框架,相关资料真的是少得可怜,所幸的是官方文档还算详细。本博文主要列举一些个人感觉比较常用的场景及相应的Mapper SQL写法,希望能够对大家有所帮助。
不少持久层框架对动态SQL的支持不足,在SQL需要动态拼接时非常苦恼,而Mybatis很好地解决了这个问题,算是框架的一大亮点。对于常见的场景,例如:批量插入/更新/删除,模糊查询,多条件查询,联表查询,