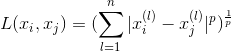[统计学习方法]K近邻法

1.K近邻算法（K-NN）

给一个点，现在希望找出距离某个点最近的K个点，这个是很有意义的，因为这样可以知道该点属于哪一类（看距离他近的点大多属于哪类）。所以其实该算法也就是一种预处理数据，以此来加速查询。

如果用式子来表示，那就是（假设决策规则为多数表决规则）：

其中I()函数表示的是判断括号内真假的函数，如果真时为1，假时为0，该式子的意思是，寻找距离x最近的k个点（即），看这k个点属于哪一类最多，就输出那个点(c_j)。

当然，当k=1时，情况最特殊，也就是该点的类型只由离他最近的那个点的类型所决定，称为最近邻算法。

2.K近邻模型

该模型由三个部分构成：距离度量，k的值，分类决策规则。

2.1.距离度量

我们可以自己定义所谓的距离，当然一般而言用的是欧氏距离，即：

也就是每一维的差的平方之和再开根号。

当然，更一般的称为“闵可夫斯基距离”，即

其中，当p=2的时候就是欧几里得距离，当p=1时称为曼哈顿距离，而p=正无穷时，称为切比雪夫距离，直观地说，也就是国际象棋中王从A格走到B格所要用的步数。

2.2.K值的选择

当K小时，近似误差会减小，但是估计误差会增大，也就是说，当k较小的时候，意味着预测的结果会相对更准确，因为距离它较远的点就不能对它的预测结果产生影响，但是，如果k很小时，当遇到他周围的点存在噪声时，很容易造成结果出错。

同理，当K大时，近似误差会增大，但是估计误差会减小，最极端的情况当k=N时，无论输入时啥，输出都是一样的，也就是这些训练数据中属于最多类的那类，忽略了数据中大量的有用信息。

2.2.3.分类决策规则

一般决策规则都用多数表决规则，该规则就看周围的点属于哪一类比较多，该点就属于哪一类。

2.3.kd树

现在输入一个点进行查询，我们需要知道距离这个点最近的K个点是什么，如果直接找的话速度会非常非常的慢，因此我们需要做一下预处理，也就是用某数据结构把这些数据存下来，以减少查询的复杂度，kd树就是干这个的。

2.3.1.kd树的构造

既然是要预处理，自然第一想到的是树状结构，不断的把这些点集细分，然后每一次搜索从根节点往下走，走到叶子节点就是答案（一般思路如此，但是kd树还需要有一个回溯的过程），所以按照这个思路构建一棵树，那么最理想的状况就是不断精确二分，使得这棵树每个叶子节点的深度最大值尽可能小。

因此我们可以首先设根节点含有所有的数据，对于这些数据，选出一个维度，对这个维度进行二分。为了使得二分的两部分尽可能均等，所以可以找到对于该维度来说最中间的数据（中位数），把这些数据分成两部分，左子树就是对于该维度比中位数小的所有点集，而右子树则是对于该维度比中位数大的所有点集，而该节点存储的则是等于该中位数的所有点。然后对于左子树和右子树不断的进行如此切分，最后切分到每个叶子节点都存储一个点为止。

其实可以把kd树的构造看做一个n维空间不断的被分割的过程，每一个节点代表一个分割出来的超平面，每一个节点上存储的点集表示该超平面经过的所有点，而某个节点的左子树包含了比该切分的超平面小的所有点，而某个节点的右子树包含了比该切分的超平面大的所有点。

至于每一次我选择哪一维进行切分，书上写的是从第一维到第m维不断的循环，但是循环顺序并不会影响最后算法的正确性，但是如果每一次都选择方差最大的维度进行切分的话，因为方差最大，所以数据集在该维度更分散，相对来说查询速度会更快一些（后面讨论）。

2.3.2.kd树的搜索

既然这么构造，那么在搜索时就会有一种冲动：从根节点出发，看给定数据某一维的值是比数据集的中位数小还是比中位数大，如果小，走左子树，大，走右子树，然后一直不断的这么走，直到走到叶子节点为止。而这种想法大体上并没有错，但是不够精确。

注意由于构造kd树时，最后切分出来的所有n维空间并不是代表与某一个节点最近的空间，因此我们不能够简单的从根节点搜索到叶子节点就宣称找到了最近的点，所以需要进行回溯操作。

因为我们已经走到了叶子节点，这时候已经有了一个目前距离最近的点和最近的距离，所以这时候从叶子节点往根节点走，每走到一个节点上都需要判断一下另外一个子树所构成的空间和查询的点的最短距离是不是比目前维护的最近距离小，如果比目前维护的最近距离还小，那么还需要到另外一个子树里找找，不然的话，另外那个子树就可以舍弃不管，在另一个子树的找法和之前递归的找法是一样的。

所以可以看出如果这个数据故意要跟你作对的话，那么可能你在查询的时候可能会有每次都要到另外一个子树里去找找，这样最坏情况下复杂度是O(n)，但是在一般情况下复杂度会是O(logn)，因为每次舍弃了一半的数据不找。

而前面说到，如果每一次都选择方差大的维度，那么对于查询来说，回溯的可能性就会少一点，那是因为如果先分割方差最大的维度，那么这样的话在走到叶子节点的时候最短距离的长度可能会变长，也就更有可能在回溯的过程当中跑到另外一个子树里去搜索，这样查询的速度会变慢。