四元数
i*i = j*j = k*k= -1
i*j = k, j*i = -k
可以把quaternion看做一个标量和一个3D向量的组合。实部w表示标量,虚部表示向量标记为V,或三个单独的分量(x,y,z)。所以quaternion可以记为[ w, V]或[ w,(x,y,x)]。对quaternion最大的误解在于认为w表示旋转角度,V表示旋转轴。正确的理解应该是w与旋转角度有关,v与旋转轴有关。例如,要表示以向量N为轴,轴旋α度,相对的quaternion应该是:
q = [ cos(α/ 2) , sin(α/ 2) N]
=[ cos(α/ 2) , ( sina(α/ 2) Nx, sin(α/ 2)Ny, sin(α/ 2)Nz ) ]
写的更清楚一点就是:Q = cos (angle/2) + i (x * sin(a/2)) + j (y * sin(a/2)) + k(z * sin(a/2))
为了计算方便,一般要求N为单位矢量。对quaternion来说使用四个值就能记录旋转,而不是Matrix所需的十六个值。为什么用quaternion来计算旋转很方便呢?先说过quaternion是一个复数,如果你还记得一点点复数的知识,那么应该知道复数乘法(叉乘)的几何意义实际上就是对复数进行旋转。对最简单的复数p= x + yi来说,和另一个复数q = ( conα,sinα)相乘,则表示把p沿逆时针方向旋转α:p’ = pq
当然,x+yi的形式只能表示2D变换,对3D变换来说就需要使用 quaternion了,而且计算也要复杂一点。为了对3D空间中的一个点p(x,y,z)进行旋转,需要先把它转换为quaternion形式p = [0, ( x, y, z)],接下来前面讨论的内容,定义q = cos(α/ 2) , sin(α/ 2) N为旋转quaternion,这里N为单位矢量长度的旋转轴,α为旋转角度。那么旋转之后的点p’则为:
p’ = qpq-1
ps:粗体字母表示矢量
///////////////////////////////////////////////////////////////////
a. 这是一篇讲解四元数原理的论文翻译,原文参见 这里。
b. 在此之前在网络上找过很多资料,但基本都是结论性的介绍,并未对”为什么“进行深入全面的解释。因此在看完本文并消化理解了以后,我决定将其翻译出来,一方面作为知识总结,一方面为相似境遇的朋友提供帮助。
c. 但并不是说这篇翻译就没什么错误。尤其是在介绍四元数历史的那节,由于缺少必要的数学涵养,我不自信是否翻得正确,还请各位朋友帮忙校准。另外由于英文水准有限,许多地方翻得比较生硬,望请诸位海涵。
d. 文中( 注: ... ) 的部分,是我根据上下文自己进行的推理,不代表作者观点(实际上作者在那些地方什么都没有说,有时候你得自己推一推才能弄明白)。
e. 由于精力和时间关系,我没有翻译全文,只是节选了重要的章节。但相信已经覆盖了必要的四元数的知识,足以支持你完成一个相机系统(Camera System)
f. 之所以说”足以“,是因为我已经用这些理论写完了一个以四元数为支撑的相机。
g. 从开始有想法对它一探究竟,到一步步实现功能,再到总结性地翻译本文,每晚见缝插针挤出约2小时,总共历时近三个月完成。时间之久,身心俱疲。Snake is Old...
-------------------------------------------
四元数
Ken Shoemake
Department of Computer and Information Science
University of Pennsylvania
Philadelphia, PA 19104
概要
凡是图形学所涉及到的数学知识,大多数都有详尽完备的介绍,但四元数却是一个例外。本文因此而写。这篇教程介绍了诸如“什么是四元数”、“为何它如此有用”、“怎么用、用在哪里”,以及“使用时机”等话题。
介绍
在图形学领域,四元数一般用来表达旋转和朝向的概念。在1985年的SIGGRAPH会议上,四元数曲线(quaternion curve) 方法第一次被引入到图形学中,意图使旋转动画(rotation animation)计算变得更加方便。虽然这只是一个相当特殊的案例,但由于四元数出色的表现,令它无论与主流的矩阵表示法相比,还是与小众的欧拉角(Euler angles)表示法相比,都不输分毫。
四元数由此声名大噪,开始作为一种新技术被应用到曲线方法以及众多领域中,如基于物理的建模技术,约束系统(constraint system)以及用户界面(user interface)上。四元数之所以能被广泛应用,是因为就实现而言,与其他同类技术相比,它不仅更加简洁,成本更低,而且更加优雅。不过,研究者和开发者想要掌握它,必须要学习一些新的数学知识,但一般的数学课或者科学课程却都不教授四元数。总之不管怎么说,无论是站在齐次坐标(homogeneous coordinates)的角度看,还是从一个更宽泛的角度看,四元数都不单单是我们所熟知的四维齐次坐标(four-component homogeneous coordinates)的复杂升级版本。
四元数定义
四元数有好几种定义的方式,这些方式的形态也许有所不同,但实质却彼此等价。了解这些形态是必要的,因为每一种形态对我们都非常有用。历史上, Hamilton首次将四元数定义为形如广义复数的形式: w+ix+jy+kz , 其中,i2 = j2 = k2 = -1,ij = k = -ji ,并且,i,j,k为虚数,而w,x,y,z为实数,(数学家为了纪念Hamilton,用H表示四元数)。四元数的运算中有一个非常特例:乘法的不可交换性。其余的运算性质则与实数的大同小异。Hamilton就曾意识到可以用这种“相似性”来抽象四元数的特性,具体说就是将四元数简单地看作一个由四个实数组成的集合[x, y, z, w],并适当地为其定义加法和乘法。然而适逢当时复数的出现,Hamilton就将(x,y,z)“打包”成虚部(Imaginary part),并以术语“向量”(vector)称之,而实数部分(Real part)他就称为“标量”(scalar)。随后的研究者们(主要是Gibbs)直接借用了Hamilton发明的这些术语,并从四元数那脏兮兮、但却很常规的运算法则中提炼出一套更“干净”的法则(extracted from the clean operations of quaternion arithmetic the somewhat messierÑbut more generalÑoperations of vector arithmetic):即现在的教学课程里都会教授的点积(dot products)与叉积(cross products)运算。对今天的我们而言,我们可以很容易逆观历史,用现代的点积、叉积等概念来描述当时的四元数。
基于以上观点,我们现在来给出一些事实:首先我们一般会这样定义四元数:[v, w], 其中v是一个向量且等于(x, y, z), 而w是一个实数。假设一个实数s, 如果用四元数形式描述的话,它就等于[0, s],而一个纯向量v,如果用四元数描述的话,则是[v,0]。 接下来我们给出四元数的一些基本运算法则:
注意 N(q)是一个标量,所以q的倒数定义很清晰(so the description of q-1 is well-defined)。另外,乘法的不可交换性导致了一些运算需要换用更加清晰的形式来表达( Otherwise, the non-commutativity of multiplication requires explicit expressions),例如要用 pq-1 来代替 p/q。
上面列出的运算公式中,即有运算本身的定义,也有由定义推导得出的结论。试着将这些结论当作定理推导一番是很有用的,而且不难:每一个证明应该都可以直截了当地计算出来。
用四元数表示旋转
四元数和三维空间内的旋转关系可以用定理1进行阐述。
定理1:令p为三维(投影)空间内的一个点,用齐次坐标将其表示成四元数的形式即为: p = (x:y:z:w) = [(x, y, z), w] = [v, w] ; 令q为任一非零四元数。那么:
- 结论1) 表达式 qpq-1的结果将使p=[v, w]变换到p`=[v`, w], 二者模长相等。
- 结论2) 任何非零实数与q相乘,上式仍然成立。
- 结论3) 如果上式中的q为N(q) = 1(即q为单位四元数),那么q = [ v sinΩ , cos Ω ] 表示一个旋转动作:将p沿着单位轴v 旋转2Ω即得到p'。
证明:让我们先从结论2入手。这个结论很容易证明。由于sq的倒数是q-1s-1, 且注意标量的乘法满足交换律,所以我们可以得到:
(sq)·p·(sq)-1 = sq·p·q-1s-1 = qpq-1ss-1 = qpq-1
根据这条结论,我们就可以把这个q直接当作一个单位四元数来看,正如 结论3里所需要的那样,而又不失一般性。对于单位四元数q, 由于q-1 = q* ,所以我们可以将 qpq-1写作 qpq*。
现在来证明结论1就简单多了。一般来说,对一个标量进行一些变换,其结果往往仍是一个标量;类似地,对一个向量[v, 0]进行一系列变换,其结果仍是一个向量。对于任何一个四元数q,其标量部分(即实部) S(q) 可以用公式2S(q) = q + q* 提取出来。于是我们可以得到这列等式:
2S(qpq*)= (qpq*) + (qpq*)* = qpq* + qp*q*
由于四元数的乘法遵循线性规律,我们可以将公因式提出,得到:
q(p+p*)q* = q(2S(p))q* = 2S(p)[注1]
又由于四元数乘法也作用于模长(Because multiplication preserves norms,),得到N(p) = N(p')[注2]; 同时因为w没有改变,因此可得N(v) = N(v')。
(
注1: 由于2S(p)为标量,我们可以把它放到前面,得2S(p)qq*。又因为结论2已经告诉我们,在q[***]q*这种类型的式子中,q是不是单位四元数都是不影响结果的。因此我们可以将其视作一个单位四元数,这样便有q* = q-1, 因此2S(p)qq* = 2S(p)qq-1 = 2S(p) 。
注2: 所谓“Because multiplication preserves norms”,我想可以这样理解:因为p' = qpq*,而因为乘法保留模长,同时我们已把q看作为单位四元数(意味着N(q)=N(q*)=1),因此有N(p') = N(p)。 再注意到上面刚刚证明了2S(p') = 2S(p),即意味着w部相同。两个四元数模长相等,其实部又相等,可以不难得到其虚部模长也相等,即N(v) = N(v')。
)
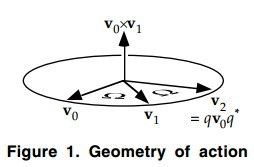
最后我们来证明结论3 —— 该定理最核心的部分。考虑下图中的情形,图中N(v0) = N(v1) = 1 。 我们定义一个四元数q =v1v0* = [v0 × v1, v0 · v1][注3] 。我们再定义Ω为v0到v1之间的角度, 所以v0·v1 = cosΩ 。我们再在两向量的叉积方向上再设置一个单位向量 v = (v0 × v1) /‖v0 × v1‖, 该单位向量同时垂直于v0 和v1。现在我们可以将q 写成 [ vsinΩ, cosΩ][注4] (我们应该假设v1 ≠ ±v0, 否则 q =+ 1, 如此这个旋转动作是无效的)(We shall assume v1 ±v0, else q = ±1, and the action is the identity)。
(
注3: 这里解释一下为什么 v1v0* = [v0 × v1, v0 · v1]。 根据前面列出的关于四元数的basic facts,我们知道而v0*= [v0, 0]* = [-v0, 0] = -v0 。同时还知道vv' = [v×v', -v·v'] ,这里令v = v1, v' = v0*。 因此得到v1v0* = (-1)v1v0 = (-1)[v1 × v0, -v1 · v0] = [v0 × v1, v0 · v1] 。
注4: 这里解释一下为什么q可以写成 [ v sinΩ, cosΩ]. 至此,我们已经知道q = v1v0*= [v0 × v1, v0 · v1] 。 很明显v0 · v1 = cosΩ 。 而又有 v0 × v1 = v · ‖v0 × v1‖。 ‖v0 × v1‖是向量积v0 × v1的模长,根据向量积的求模共识,我们有 ‖v0 × v1‖ = ‖v0‖‖v1‖sinΩ, 因为v0、v1皆为单位向量,所以‖v0 × v1‖ =