Codeforces Round #341 (Div. 2) 解题报告

621A-Wet Shark and Odd and Even

                time limit per test2 seconds    memory limit per test256 megabytes

Today, Wet Shark is given n integers. Using any of these integers no more than once, Wet Shark wants to get maximum possible even (divisible by 2) sum. Please, calculate this value for Wet Shark.

Note, that if Wet Shark uses no integers from the n integers, the sum is an even integer 0.

Input
The first line of the input contains one integer, n (1 ≤ n ≤ 100 000). The next line contains n space separated integers given to Wet Shark. Each of these integers is in range from 1 to 109, inclusive.

Output
Print the maximum possible even sum that can be obtained if we use some of the given integers.

input
3
1 2 3
output
6

input
5
999999999 999999999 999999999 999999999 999999999
output
3999999996

Note
In the first sample, we can simply take all three integers for a total sum of 6.

In the second sample Wet Shark should take any four out of five integers 999 999 999.

题目链接：cf-621A

题目大意：给出n个数，求着n个数相加和为偶数的最大值

题目思路：水题

以下是代码：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n;
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        long long x;
        cin >> x;
        if (x & 1) k = min(k,x);  //找出最小的偶数
        s += x;
    }
    if (s & 1) s -= k;  //把最小的偶数减去 
    cout << s;
}

621B-Wet Shark and Bishops

            time limit per test2 seconds        memory limit per test256 megabytes

Today, Wet Shark is given n bishops on a 1000 by 1000 grid. Both rows and columns of the grid are numbered from 1 to 1000. Rows are numbered from top to bottom, while columns are numbered from left to right.

Wet Shark thinks that two bishops attack each other if they share the same diagonal. Note, that this is the only criteria, so two bishops may attack each other (according to Wet Shark) even if there is another bishop located between them. Now Wet Shark wants to count the number of pairs of bishops that attack each other.

Input
The first line of the input contains n (1 ≤ n ≤ 200 000) — the number of bishops.

Each of next n lines contains two space separated integers xi and yi (1 ≤ xi, yi ≤ 1000) — the number of row and the number of column where i-th bishop is positioned. It’s guaranteed that no two bishops share the same position.

Output
Output one integer — the number of pairs of bishops which attack each other.

input
5
1 1
1 5
3 3
5 1
5 5
output
6

input
3
1 1
2 3
3 5
output
0

Note
In the first sample following pairs of bishops attack each other: (1, 3), (1, 5), (2, 3), (2, 4), (3, 4) and (3, 5). Pairs (1, 2), (1, 4), (2, 5) and (4, 5) do not attack each other because they do not share the same diagonal.

题目链接：cf-621B

题目大意：如图，求在同一对角线的两点，有多少对。

题目思路：我的思路是直接暴力所有的对角线，代码比较丑。看了别人的代码，思路好棒！

更好的做法：

以下是代码：

#include<iostream>
#include<map>
using namespace std;
map<int,long long>a,b;
int main()
{
    int n,x,y;
    long long ans=0;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        cin>>x>>y;
        ans+=a[x-y]+b[x+y];
        a[x-y]++;
        b[x+y]++;
    }
    cout<<ans<<endl;
}

我的做法：直接暴力所有对角线。（写了好久，绕晕了。。）

#include <vector>
#include <map>
#include <set>
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <string>
#include <cstring>
using namespace std;
int g[1005][1005];
int main(){
    int n = 1000;
    int t;
    cin >> t;
    for (int i = 0; i < t; i++)
    {
        int x,y;
        cin >> x >> y;
        g[x][y] = 1;
    }
    long long ans = 0;
    for (int i = 0; i < n; i++)
    {
        long long ret = 0;
        for (int j = 1; (j + i) <= n; j++)
        {
            if (g[j][j + i] == 1) ret++;
        }
        ans += (ret - 1) * ret / 2;
    }
    for (int i = 1; i < n; i++)
    {
        long long ret = 0;
        for (int j = 1; (j + i) <= n; j++)
        {
            if (g[j + i][j] == 1) ret++;
        }
        ans += (ret - 1) * ret / 2;
    }

    for (int i = 0; i < n; i++)
    {
        long long ret = 0;
        for (int j = 1,k = j + i; k > 0; j++,k--)
        {
            if (g[j][k] == 1) ret++;
        }
        ans += (ret - 1) * ret / 2;
    }

    for (int i = 1; i < n; i++)
    {
        long long ret = 0;
        for (int j = 1 + i,h = n; h > 0 && j <= n; j++,h--)
        {
            if (g[j][h] == 1) ret++;
        }
        ans += (ret - 1) * ret / 2;
    }
    cout << ans << endl;
    return 0;
}

621C-Wet Shark and Flowers

                time limit per test2 seconds    memory limit per test256 megabytes

There are n sharks who grow flowers for Wet Shark. They are all sitting around the table, such that sharks i and i + 1 are neighbours for all i from 1 to n - 1. Sharks n and 1 are neighbours too.

Each shark will grow some number of flowers si. For i-th shark value si is random integer equiprobably chosen in range from li to ri. Wet Shark has it’s favourite prime number p, and he really likes it! If for any pair of neighbouring sharks i and j the product si·sj is divisible by p, then Wet Shark becomes happy and gives 1000 dollars to each of these sharks.

At the end of the day sharks sum all the money Wet Shark granted to them. Find the expectation of this value.

Input
The first line of the input contains two space-separated integers n and p (3 ≤ n ≤ 100 000, 2 ≤ p ≤ 109) — the number of sharks and Wet Shark’s favourite prime number. It is guaranteed that p is prime.

The i-th of the following n lines contains information about i-th shark — two space-separated integers li and ri (1 ≤ li ≤ ri ≤ 109), the range of flowers shark i can produce. Remember that si is chosen equiprobably among all integers from li to ri, inclusive.

Output
Print a single real number — the expected number of dollars that the sharks receive in total. You answer will be considered correct if its absolute or relative error does not exceed 10 - 6.

Namely: let’s assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if .

input
3 2
1 2
420 421
420420 420421
output
4500.0

input
3 5
1 4
2 3
11 14
output
0.0

题目链接：cf-621C

题目大意：给出n个数（成环），相邻两个点的乘积是p的倍数，则两个点分别获得1000分。问最后分数的期望，每个点给了[l,r]的范围。

题目思路：E = sum (1000 * 乘积是p的倍数的概率)

以下是代码：

#include <vector>
#include <map>
#include <set>
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <string>
#include <cstring>
using namespace std;
double p[100010];
int main(){
    long long n,prm;
    cin >> n >> prm;
    for (int i = 1; i <= n; i++)
    {
        long long l,r;
        cin >> l >> r;
        p[i] = (r / prm - (l - 1) / prm) * 1.0 / (r - l + 1);  //计算出第i个数是prm的整数倍的概率 
    }
    double ans = 0;
    p[0] = p[n];
    for (int i = 0; i <= n; i++)
    {
        if (i < n) ans += p[i] + (1 - p[i]) * p[i + 1];  //第i个数是prm的倍数 or 第i+1个数是prm的倍数 
        if (i > 0) ans += p[i] + (1 - p[i]) * p[i - 1];
    }
    printf("%.8f\n",ans * 1000);
    return 0;
}

621D- Rat Kwesh and Cheese

                time limit per test2 seconds    memory limit per test256 megabytes

Wet Shark asked Rat Kwesh to generate three positive real numbers x, y and z, from 0.1 to 200.0, inclusive. Wet Krash wants to impress Wet Shark, so all generated numbers will have exactly one digit after the decimal point.

Wet Shark knows Rat Kwesh will want a lot of cheese. So he will give the Rat an opportunity to earn a lot of cheese. He will hand the three numbers x, y and z to Rat Kwesh, and Rat Kwesh will pick one of the these twelve options:

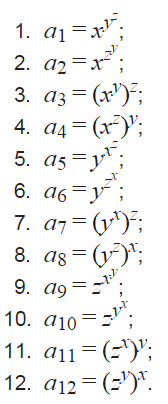
Let m be the maximum of all the ai, and c be the smallest index (from 1 to 12) such that ac = m. Rat’s goal is to find that c, and he asks you to help him. Rat Kwesh wants to see how much cheese he gets, so he you will have to print the expression corresponding to that ac.

Input
The only line of the input contains three space-separated real numbers x, y and z (0.1 ≤ x, y, z ≤ 200.0). Each of x, y and z is given with exactly one digit after the decimal point.

Output
Find the maximum value of expression among x^y^z, x^z^y, (x^y)^z, (x^z)^y, y^x^z, y^z^x, (y^x)^z, (y^z)^x, z^x^y, z^y^x, (z^x)^y, (z^y)^x and print the corresponding expression. If there are many maximums, print the one that comes first in the list.

xyz should be outputted as x^y^z (without brackets), and (xy)z should be outputted as (x^y)^z (quotes for clarity).

input
1.1 3.4 2.5
output

z^y^x
input
2.0 2.0 2.0
output
x^y^z

input
1.9 1.8 1.7
output
(x^y)^z

题目链接：cf-621D

题目大意：给出12种表达式，以及x,y,z三个数字。求把数字代入表达式之后，哪个结果最大。输出该表达式

题目思路：思路很简单，就是代入计算。但是存在难点：数字太大。

解决方法：
1. 必须以log对所有式子取对数来缩小答案大小。
2. 对取对数处理后的式子仍要用long double运算

参考博客：here

以下是代码：

#include <vector>
#include <map>
#include <set>
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <string>
#include <cstring>
using namespace std;
long double num[20];
long double x,y,z;
string s[15] = {
    "x^y^z",  
    "x^z^y",  
    "(x^y)^z",  
    "(x^z)^y",  
    "y^x^z",  
    "y^z^x",  
    "(y^x)^z",  
    "(y^z)^x",  
    "z^x^y",  
    "z^y^x",  
    "(z^x)^y",  
    "(z^y)^x" 
};
int main(){
    cin >> x >> y >> z;
    num[0]= powl(y, z) * log(x);   // x^y^z 
    num[1]= powl(z, y)*log(x);   // x^z^y 
    num[2]= num[3] = y * z * log(x);   // (x^y)^z (x^z)^y =x^(y*z) 
    num[4]= pow(x, z) * log(y);   // y^x^z 
    num[5]= pow(z, x) * log(y);   // y^z^x 
    num[6]= num[7] = x * z * log(y);   // (y^x)^z (y^z)^x =y^(x*z) 
    num[8]= pow(x, y) * log(z);   // z^x^y 
    num[9]= pow(y, x) * log(z);   // z^y^x 
    num[10]= num[11] = x * y * log(z); // (z^x)^y (z^y)^x =z^(x*y) 
    int poi = 0;
    for (int i = 1; i < 12; i++) 
    {
        if (num[i] > num[poi]) poi = i;
    }
    cout << s[poi] << endl;
    return 0;
}

E. Wet Shark and Blocks

There are b blocks of digits. Each one consisting of the same n digits, which are given to you in the input. Wet Shark must choose exactly one digit from each block and concatenate all of those digits together to form one large integer. For example, if he chooses digit 1 from the first block and digit 2 from the second block, he gets the integer 12.

Wet Shark then takes this number modulo x. Please, tell him how many ways he can choose one digit from each block so that he gets exactly k as the final result. As this number may be too large, print it modulo 109 + 7.

Note, that the number of ways to choose some digit in the block is equal to the number of it’s occurrences. For example, there are 3 ways to choose digit 5 from block 3 5 6 7 8 9 5 1 1 1 1 5.

Input
The first line of the input contains four space-separated integers, n, b, k and x (2 ≤ n ≤ 50 000, 1 ≤ b ≤ 109, 0 ≤ k < x ≤ 100, x ≥ 2) — the number of digits in one block, the number of blocks, interesting remainder modulo x and modulo x itself.

The next line contains n space separated integers ai (1 ≤ ai ≤ 9), that give the digits contained in each block.

Output
Print the number of ways to pick exactly one digit from each blocks, such that the resulting integer equals k modulo x.

input
12 1 5 10
3 5 6 7 8 9 5 1 1 1 1 5
output
3
input
3 2 1 2
6 2 2
output
0
input
3 2 1 2
3 1 2
output
6

题目链接：cf-621E

题目大意：给出n个数字，每次选一个数字，选b次，问得到的数字取余x等于k的情况数有多少种

题目思路：因为每次状态转移都是一样的，所以可用矩阵快速幂

以下是代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef vector<ll> vec;
typedef vector<vec> mat;
#define M 1000000007
//计算A * B
mat mul(mat &A, mat &B)
{
    mat C(A.size(), vec(B[0].size()));
    for (int i = 0; i < A.size(); i++)
    {
        for (int k = 0; k < B.size(); k++)
        {
            for (int j = 0; j < B[0].size(); j++)
            {
                C[i][j] = (C[i][j] + A[i][k] * B[k][j]%M)%M;
            }
        }
    }
    return C;
} 
//计算A^n
mat pow(mat A, ll n)
{
    mat B(A.size(), vec(A.size()));
    for (int i = 0; i < A.size(); i++) B[i][i] = 1;
    while(n > 0)
    {
        if (n & 1) B = mul(B, A);
        A = mul(A, A);
        n >>= 1;
    }
    return B;
} 
int a[15]={0};
int main()
{
    int n, b, k, x;
    cin >> n >> b >> k >> x;
    for( int i=0 ; i<n ; i++ ){
        int s;
        scanf("%d", &s);
        a[s]++;
    }
    mat A(x+2, vec(x+2));
    for (int i = 0; i < x; i++) //上一次取余x后的余数
    {
        for (int j = 0; j < 10; j++) //这一次的末位
        {
            A[(i * 10 + j) % x][i] += a[j]; //j这个数字在数组中出现的次数 
        }
    }
    A = pow(A, b);
    cout << A[k][0]%M << endl;
    return 0;
}