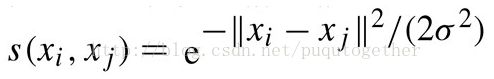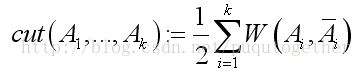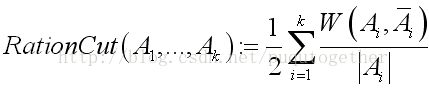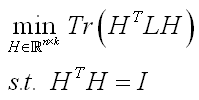谱聚类
摘要
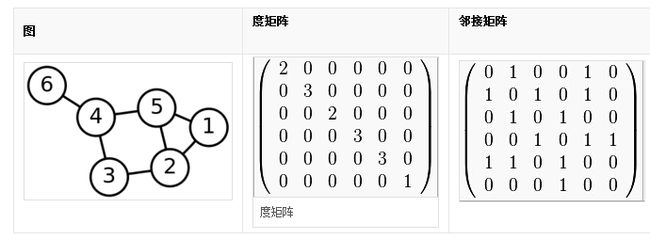
度矩阵邻接矩阵
度矩阵为对角矩阵,度为与节点的相连的个数
特征值 与 特征向量
设 A 是n阶方阵,如果存在数m和非零n维列向量 x,使得 Ax=mx 成立,则称 m 是A的一个特征值(characteristic value)或本征值,x 称为特征向量
拉普拉斯矩阵
图论的数学领域中的拉普拉斯矩阵(也被称为导纳矩阵,吉尔霍夫矩阵或离散拉普拉斯)是图的矩阵表示。
拉普拉斯矩阵 结合 吉尔霍夫理论 可以用来计算图的最小生成树的个数。拉普拉斯矩阵还可用来寻找图的其他属性:谱图理论spectral graph theory.
黎曼几何的Cheeger不等式有涉及了拉普拉斯矩阵的离散模拟。这或许是谱图理论中最重要的定理也是在算法应用中最有用的facts.它通过拉普拉斯矩阵的第二特征值来近似图的最小割。
拉普拉斯矩阵是 度矩阵 和 邻接矩阵的差。度矩阵是一个对角矩阵,其包含了每个顶点的度。在处理有向图时,根据应用来选择入度或出度。
理解谱聚类
前面介绍过K-means聚类方法,这个方法简单易懂,主要在于如何定义距离计算公式(一般使用欧氏距离),如何选择K值,这两个问题。这次我们介绍谱聚类,它是K-means的升级版。我们计划从这样几个方面介绍谱聚类:K-measn聚类有什么缺点?谱聚类的基本思想,以及谱聚类的算法步骤。
那么K-means到底有什么问题呢?我们为什么需要改进它呢~
- 当样本维数增大时,K-means的计算会困难。因为在K-means中,输入计算的是欧氏空间中的原始向量;
- K-means求得的是一种局部最优的聚类策略,SSE不一定就是最小的;
1. 谱聚类的基本思想
谱聚类是一种基于图论的聚类方法。将样本看成顶点,样本的相似度看作带权边。这样,把样本集划分成K个簇的过程就等同于一个图的分割问题。
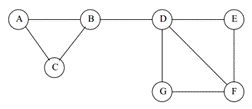
如下图所示,每个顶点是一个样本,共有7个样本(实际中一个样本是特征向量)。边的权值就是样本之间的相似度。然后我们需要分割,分割之后要使得连接不同组之间的边的权重尽可能低(组间相似度小),组内部的边的权重尽可能高(组内相似度高)。
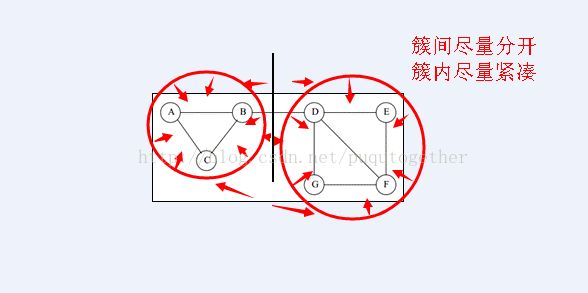
比如我们把中间的边去掉,就满足上面的簇间相似性最小,簇内相似性最大。如下图:
2. 算法步骤
谱聚类算法主要有下面这几步:
1)计算得到图的邻接矩阵E,以及拉普拉斯矩阵L;
给定样本的原始特征,我们需要计算两两样本之间的相似度值,才能构造出邻接矩阵E。我们一般使用高斯核函数来计算相似度。公式如下:
其中xi和xj是两个样本的原始特征向量,我们可以计算出它们二者之间的相关性。注意,邻接矩阵的对角线元素一致等于零。这样我们就得到了邻接矩阵E。
拉普拉斯矩阵L=D-E, 其中D为上面图的度矩阵,度是图论中的概念,也就是矩阵E行或列的元素之和。后面我们就要基于矩阵L来进行研究。
2)聚类划分准则
关于划分准则的问题是聚类技术中的核心。谱聚类被看作属于图论领域的问题,那个其划分也会和边的权重有关。
准则1:最小化进行分割时去掉的边的权重之和。
这个准则直观地让分割之后簇之间的相似度最小了。但是有个问题,就是这个准则没有考虑到簇的大小,容易造成一个样本就能分为一个簇。为了避免这个问题,有了下面的准则。
准则2:考虑簇的大小。
这个准则2相比于准则1的改进,类似于C4.5中的增益比率和ID3的信息增益的改进。在RatioCut中,如果某一组包含的顶点数越少,那么它的值就越大。在一个最小化问题中,这相当于是惩罚,也就是不鼓励将组分得太小。现在只要将最小化RatioCut解出来,分割就完成了。不幸的是,这是个NP难问题。想要在多项式时间内解出来,就要对这个问题作一个转化了。在转化的过程中,就用到上面提到的L的那一组性质,经过若干推导,最后可以得到这样的一个问题:
这个问题和线性鉴别分析LDA中的目标函数转化过程类似。这个问题可以转化为特征分解,我们对拉普拉斯矩阵L做特征分解,取前k个最小的特征值对应的特征向量,这些k个特征向量组成了新的样本特征矩阵,维数为N*k.
接下来,我们N*k的矩阵的每一行都看作k维空间中的向量,也就是每个样本现在只有k维,每一行看作一个点进行K-means聚类。聚类得到改行属于哪一个簇,那么原来的样本就属于该簇。
所以说,谱聚类的聚类过程只需要数据之间的相似度矩阵就可以,而K-means聚类是拿样本的原始特征向量来聚类,这是它们的不同。