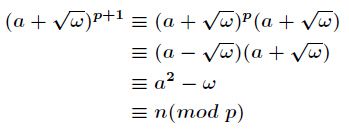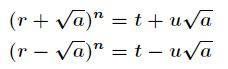二次同余方程的解

今天要讨论的问题是解方程，其中是奇质数。

 

引理：

 

证明：由费马小定理，

 

引理：方程有解当且仅当

 

定理：设满足不是模的二次剩余，即无解，那么是二次

     剩余方程的解。

 

证明：由，前面的等号用二项式定理和，后面的等

     号用了费马小定理和是模的二次非剩余。然后

 

      

 

在算法实现的时候，对的选择可以随机，因为大约有一半数是模的二次非剩余，然后快速幂即可。

 

 

题目：http://acm.timus.ru/problem.aspx?space=1&num=1132

 

题意：求二次同余方程的解。

 

代码：

#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;
typedef long long LL;

LL quick_mod(LL a, LL b, LL m)
{
    LL ans = 1;
    a %= m;
    while(b)
    {
        if(b & 1)
        {
            ans = ans * a % m;
            b--;
        }
        b >>= 1;
        a = a * a % m;
    }
    return ans;
}

struct T
{
    LL p, d;
};

LL w;

//二次域乘法
T multi_er(T a, T b, LL m)
{
    T ans;
    ans.p = (a.p * b.p % m + a.d * b.d % m * w % m) % m;
    ans.d = (a.p * b.d % m + a.d * b.p % m) % m;
    return ans;
}

//二次域上快速幂
T power(T a, LL b, LL m)
{
    T ans;
    ans.p = 1;
    ans.d = 0;
    while(b)
    {
        if(b & 1)
        {
            ans = multi_er(ans, a, m);
            b--;
        }
        b >>= 1;
        a = multi_er(a, a, m);
    }
    return ans;
}

//求勒让德符号
LL Legendre(LL a, LL p)
{
    return quick_mod(a, (p-1)>>1, p);
}

LL mod(LL a, LL m)
{
    a %= m;
    if(a < 0) a += m;
    return a;
}

LL Solve(LL n,LL p)
{
    if(p == 2) return 1;
    if (Legendre(n, p) + 1 == p)
        return -1;
    LL a = -1, t;
    while(true)
    {
        a = rand() % p;
        t = a * a - n;
        w = mod(t, p);
        if(Legendre(w, p) + 1 == p) break;
    }
    T tmp;
    tmp.p = a;
    tmp.d = 1;
    T ans = power(tmp, (p + 1)>>1, p);
    return ans.p;
}

int main()
{
    int t;
    scanf("%d", &t);
    while(t--)
    {
        int n, p;
        scanf("%d %d",&n,&p);
        n %= p;
        int a = Solve(n, p);
        if(a == -1)
        {
            puts("No root");
            continue;
        }
        int b = p - a;
        if(a > b) swap(a, b);
        if(a == b)
            printf("%d\n",a);
        else
            printf("%d %d\n",a,b);
    }
    return 0;
}

 

接下来我们来解另一个二次同余方程的解，其中，并且是奇质数。方法如下

 

先求出方程的一个解，那么进一步有

 

     

 

我们知道

 

      

 

那么也就是说

 

      

 

可以证明和，那么最终得到

 

       

 

这里由于不是素数，所以求逆元用扩展欧几里得算法即可。

 

 

例如：求方程的解

 

分析：利用上述方法求得，最终解得。