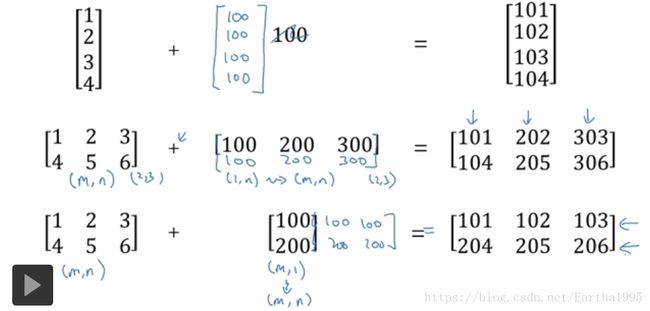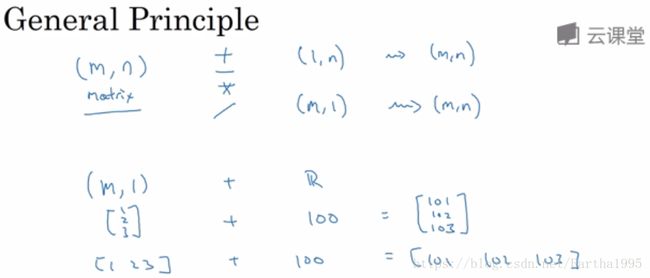吴恩达深度学习课程笔记
一、深度学习概论
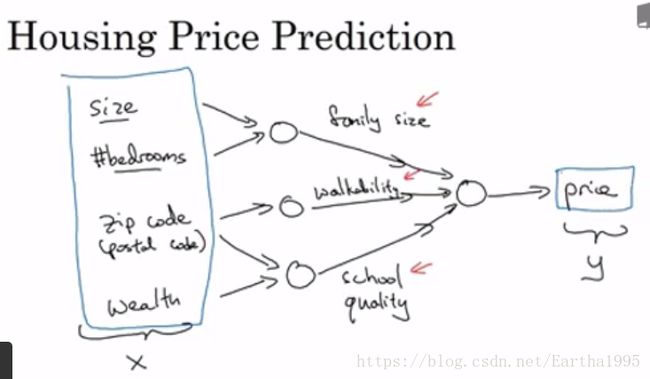
1.什么是神经网络?
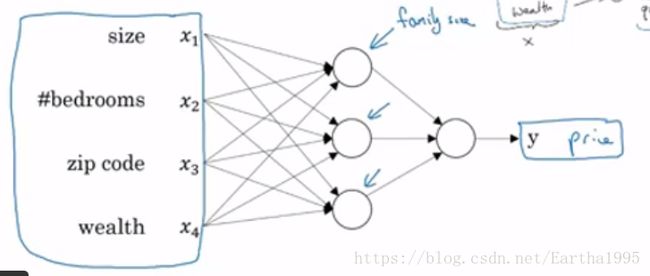
由预测房价的例子引出一个基本的神经网络结构:
2.神经网络在监督学习上的应用
结构化数据:每个特征都有着清晰的定义
非结构化数据:如音频、图像、文本等,其每个特征可以是图像中的像素或者文本中的单词。
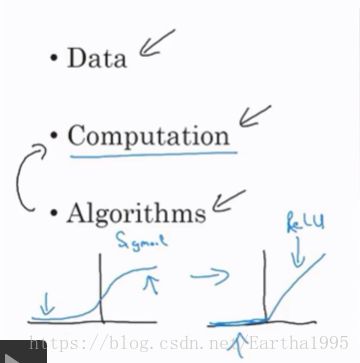
3.深度学习兴起的原因
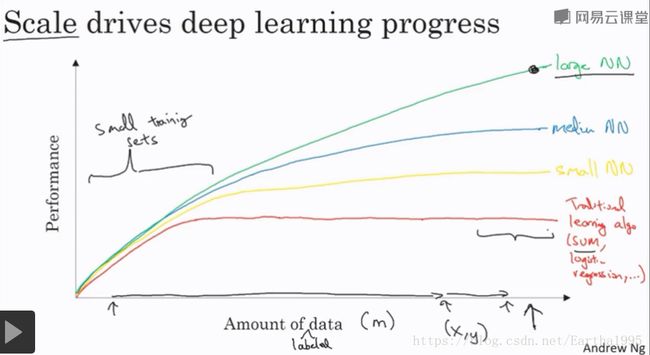
二、神经网络基础(以logistic回归为例)
1.一些符号说明及Logistic回归介绍
后面需要用到的一些符号说明:
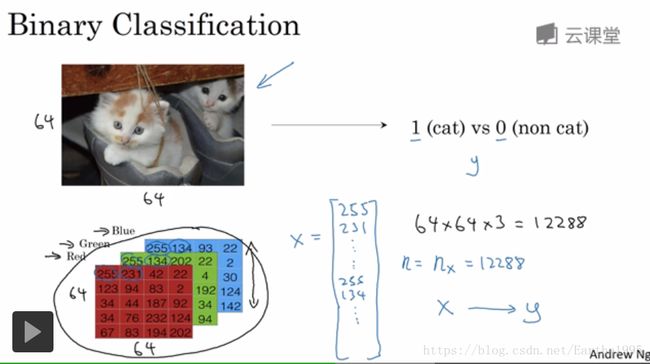
Logistic回归用于二分类问题,预测输出的概率
右上角的(i)表示第i个训练样本
Logistic回归损失函数的定义及解释(凸的便于优化)
损失函数衡量了在单个训练样本上的表现
成本函数衡量的是在全体训练集上的表现
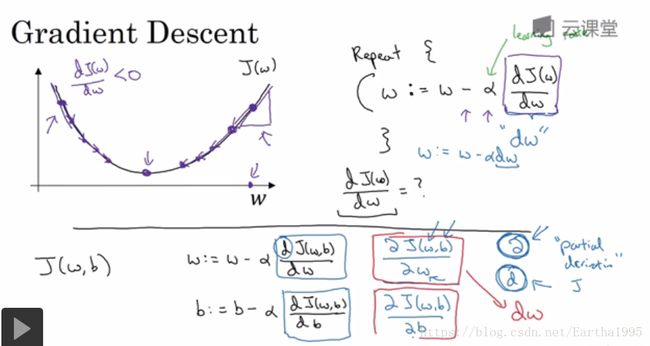
2.梯度下降法与函数导数
梯度下降法的实现方法
函数导数的介绍(跳过)
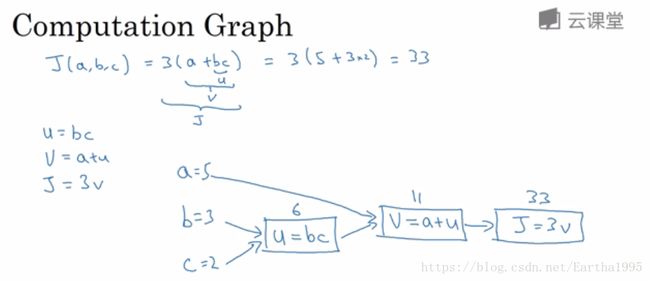
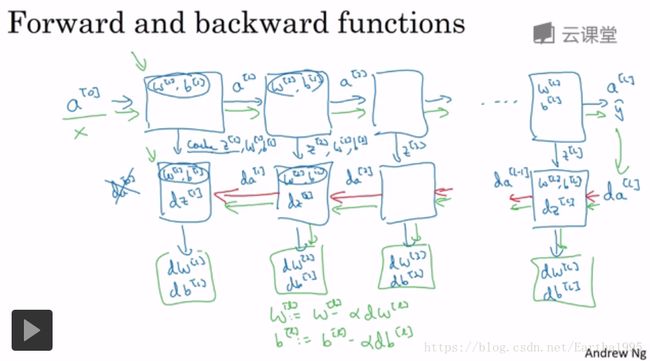
3.神经网络的前向传播与反向传播
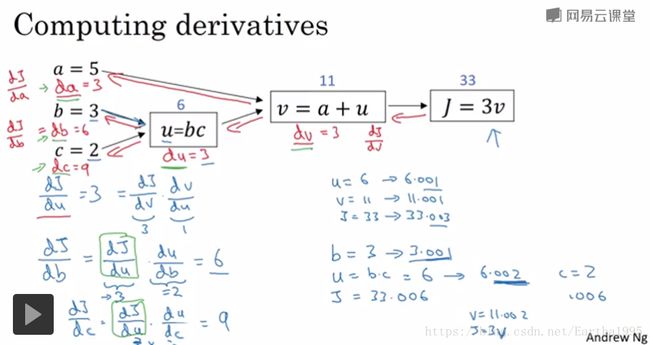
首先计算神经网络的输出,紧接着进行一个反向传输操作(用来计算对应的梯度或者导数)
注:链式法则(chain rule)求导数,反向传播写代码时直接用da表示输出对变量a的导数
4.logistic回归的梯度下降法
单个训练样本的一次梯度更新步骤
计算出dw1,dw2,db后,更新w1,w2,b
m个训练样本的一次梯度更新步骤
这里dw1,dw2,db作为累加器,计算在所有样本上的梯度
两个for循环待向量化(Vectorization):遍历所有样本,遍历样本的每个特征
5.向量化
去掉一个for循环(同时处理所有特征):
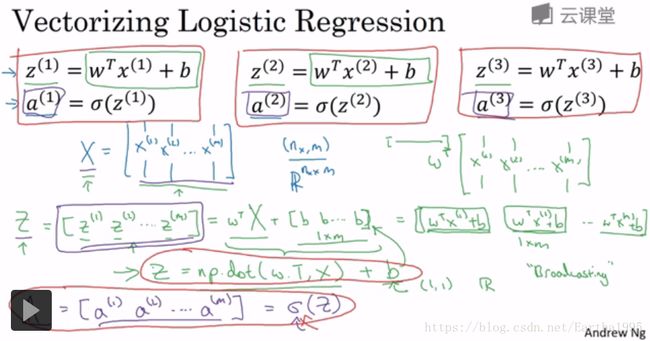
一步迭代的向量化实现(同时处理所有m个训练样本):
所有样本横向堆叠在X里
再去掉一个for循环,向量化同时计算m个训练数据的梯度:
总结:实现logistic回归的梯度下降一次迭代(完成正向和反向传播,实现对所有训练样本进行预测和求导)
6.广播(broadcasting)
广播的几个例子:广播的一些通用规则:
7.避免出错的一些小技巧
三、浅层神经网路
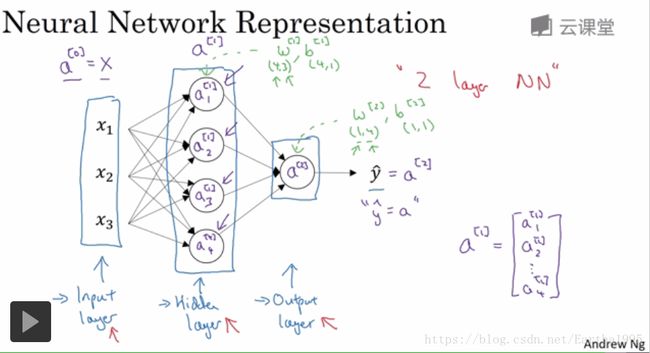
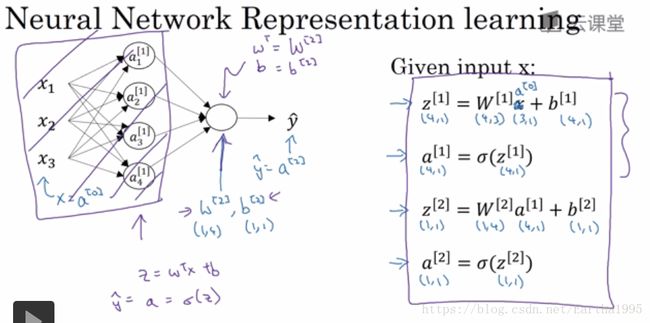
1.神经网络的表示
右上角[i]表示这些节点相关的量:层。注意与(i)相区分
直觉:神经网络类似于logistic,不过是反复计算z,a
2层神经网络:隐藏层和输出层(输入层称第0层,不包含进来)
各层参数维度的确定:对于隐藏层(4,3),有4个节点,3个输入特征
a[l]i:第l层的第i个节点
一个小圈圈执行两步计算
当我们向量化时一条经验法则:当在一层中有不同的节点,纵向堆叠起来
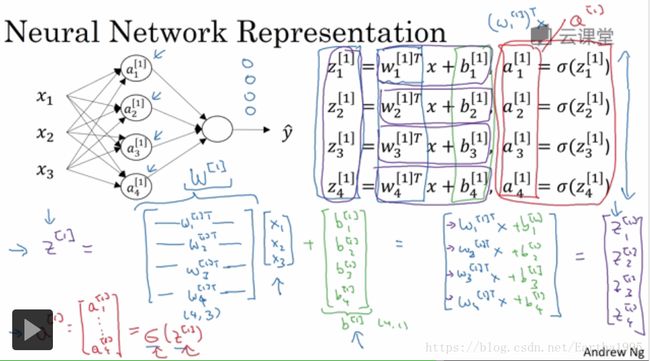
2.神经网络的输出
(1)单个训练样本
计算神经网络的输出只需要这四行代码(单个训练样本时 计算神经网络的预测)
(2)m个训练样本向量化的输出
将不同训练样本向量化
横向指标对应了不同的训练样本
竖向指标对应了神经网络里的不同节点
第一个黑点对应第一个训练样本,第一个隐藏单元的激活函数
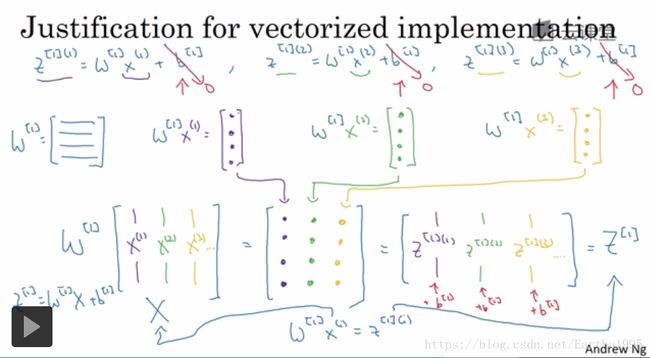
m个训练样本向量化实现的解释:
如果将输入成列向量堆叠,运算后得到成列堆叠的输出
同样的计算不断重复
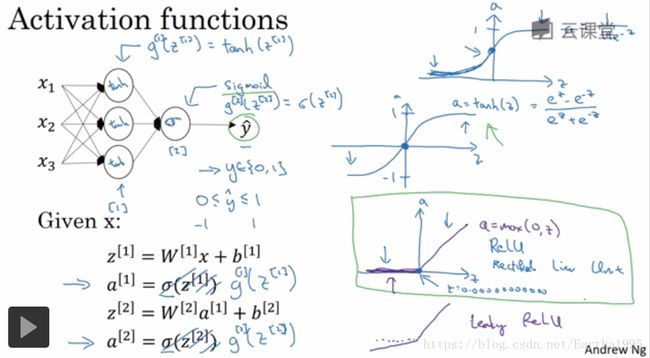
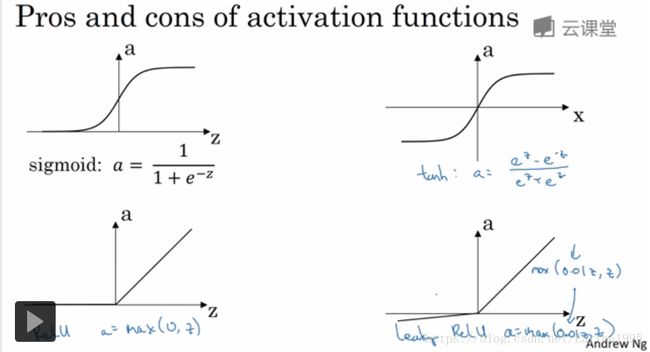
3.激活函数
tanh函数:有类似数据中心化的效果
二者都有一个缺点:当z很大或很小时梯度趋近于0,这样会拖慢梯度下降法
ReLU(修正线性单元):默认的激活函数,但当z为负时,导数等于0
leaky ReLU(带泄露的ReLU):通常比ReLU激活函数更好但使用频率没那么高
为什么需要非线性激活函数?
如果使用线性激活函数,无论你的神经网络有多少层,由于线性函数的组合还是线性函数,所以不如直接去掉全部隐藏层
激活函数的导数(略过)
4.神经网络的梯度下降法
n[0],n[1],n[2]表示各层神经元的维度
前向传播:四个等式
后向传播:六个等式
反向传播的直观理解
总结
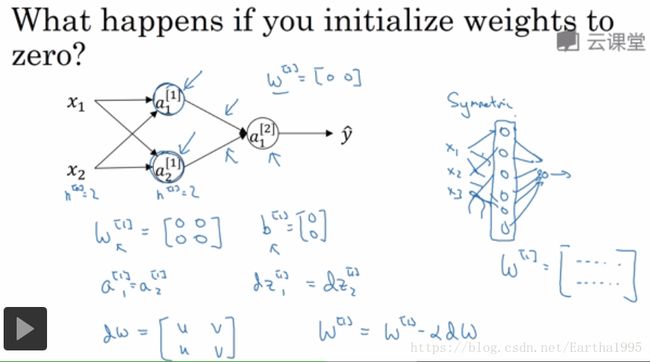
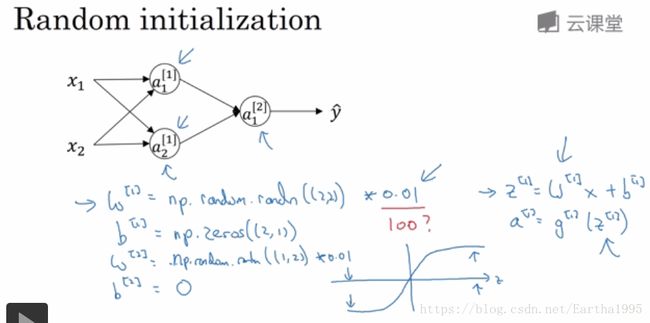
5.随机初始化
W为什么不能初始化为0矩阵
完全对称,输出的每行数值都一样
参数太大的话,激活函数接近饱和,梯度小,减慢学习速度
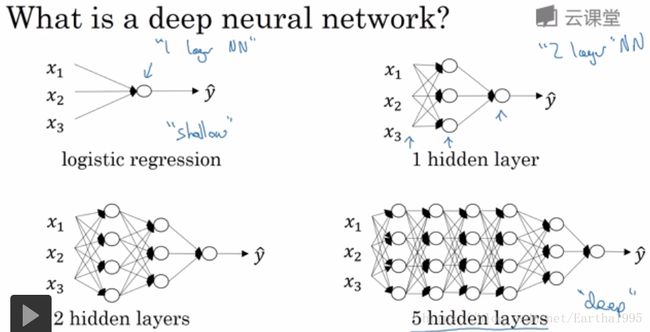
四、深层神经网络
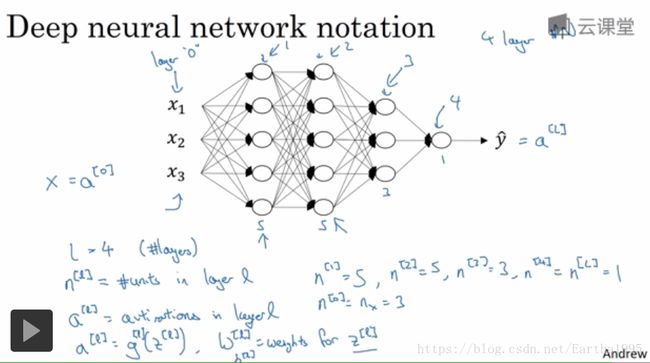
1.深层神经网络
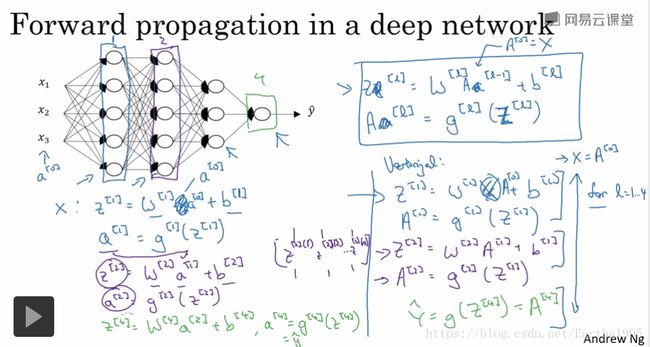
2.深层神经网络中的前向传播
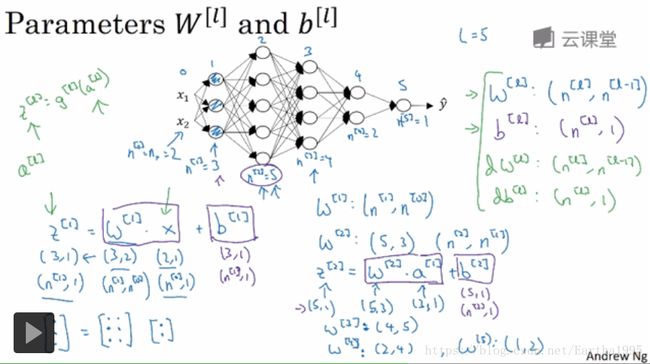
3.核对矩阵的维度
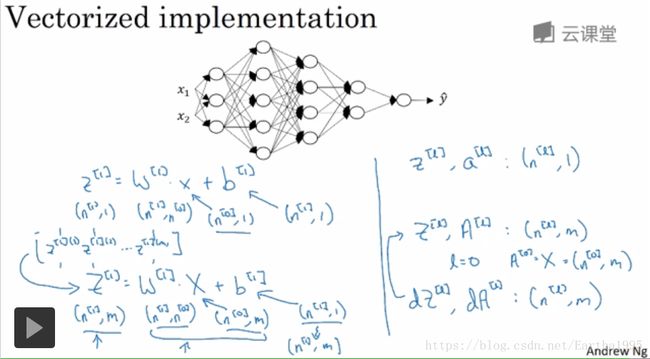
多个样本时,z,a,x的维度发生变化,Z,A,X变成m列(样本个数),反向传播d..维度与其一样:
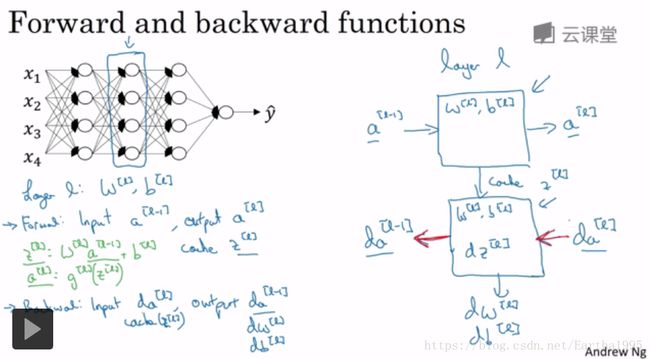
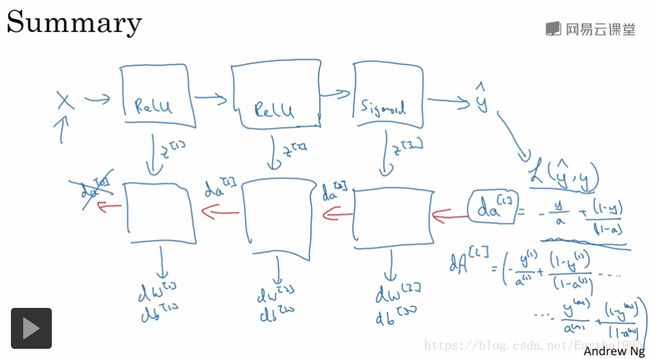
4.前向和反向传播
初始化一个向量化反向传播的方法: