拉格朗日插值法 【NOIP2017提高A组模拟10.6】Count

Description

Input

一行三个正整数 ，表示 l,r,k，含义如题所示。

Output

一行一个整数表示答案 mod 998244353。

Sample Input

2 3 1

Sample Output

5

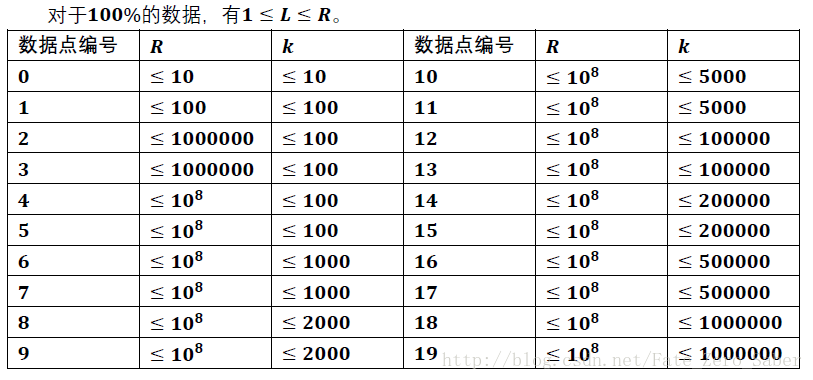
Data Constraint

拉格朗日插值

对于一个最高次幂为k的方程，我们可以用k+1个点将这个函数确定（如两点确定一个一次方程，三个点确定一个二次方程）而拉格朗日插值法实际上给出了一个在知道k+1的点的情况下求出函数每一个x对应的y的位置
给出拉格朗日插值法的公式：
假设我们已经知道了(x1,y1)…(xk,yk) 现给出x，求对应的y
y=∑k+1i=1yi∗∑k+1j=1(j<>i)Πx−xjxi−xj
这个方程的证明也比较简单
只要证明这个方程的图像过(x1,y1)…(xk,yk)就可以了
对于一个xc,yc只有在i枚举到对应的c时后面的连乘的值才不是0而是1，所以最后对应的值是yc

题解

设ans(i)表示 ∑ij=1ik 那么答案其实就是ans(r)-ans(l-1)
发现ans(i)其实是一个最高项为k+1的函数
那么我们可以先预处理出ans的前k+2项，对于后面的项直接套公式就好了

贴代码

#include
#include
#include
#include
#include
#define fo(i,a,b) for(i=a;i<=b;i++)
#define ll long long
using namespace std;

const int maxk=1e6+5,md=998244353;

ll f[maxk*2];
ll i,j,k,l,r,n,x,y,ans,sum,c1,c2,bi,mi;

ll quickmi(ll x,ll y){
    ll t1=1;
    while (y){
        if ((y & 1)==1) t1=(t1*x)%md;
        x=(x*x)%md;
        y=y/2;
    }
    return t1;
}
void yu(){
    f[1]=quickmi(2,k);
    fo(i,2,k+2)
        f[i]=(f[i-1]+quickmi(i,k))%md;
}
ll geans(ll x){
    if (x<=k+2) return f[x];
    c1=c2=1;
    fo(i,2,k+2){
        c1=(c1*(x-i))%md;
        c2=(c2*(1-i))%md;
    }
    bi=1;mi=-k-1;
    ans=(f[1]*((c1*quickmi(c2,md-2))%md))%md;
    fo(i,2,k+2){
        c1=(c1*quickmi(x-i,md-2))%md;
        c1=(c1*(x-i+1))%md;
        c2=(c2*quickmi(mi,md-2))%md;
        c2=(c2*bi)%md;
        bi++; mi++; if (mi==0) mi++;
        ans=(ans+f[i]*((c1*quickmi(c2,md-2))%md))%md;
    }
    ans=(ans+md)%md;
    return ans;
}
int main(){
    freopen("count.in","r",stdin);
    freopen("count.out","w",stdout);
    scanf("%lld%lld%lld",&l,&r,&k);
    yu();
    printf("%lld\n",(md+geans(r)-geans(l-1))%md);
    return 0;
}