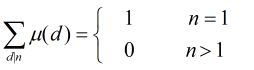FGD正在破解一段密码,他需要回答很多类似的问题:对于给定的整数a,b和d,有多少正整数对x,y,满足x<=a,y<=b,并且gcd(x,y)=d。作为FGD的同学,FGD希望得到你的帮助。
莫比乌斯函数(bzoj 1101: [POI2007]Zap)
莫比乌斯反演:
http://blog.csdn.net/acdreamers/article/details/8542292
课件:https://wenku.baidu.com/view/fbec9c63ba1aa8114431d9ac.html
(下面所有的d|n都表示d是n的约数)
莫比乌斯函数u(n)函数定义:
①u(1)==1
②若d = p1*p2*p3…pk,其中pi为质数且互不相同,那么u(n) = (-1)^k
③其他情况下u(n)==0
u(n)函数性质:
其中φ(n)是欧拉函数,表示小于n的正整数中与n互质的数的数目(φ(1)=1)
莫比乌斯反演公式:
令F[n]和f[n]是定义在非负整数集合上的两个函数,并且满足条件
那么有
附录:
若f[n]为积性函数:
①f[1] = 1
②f[xy] = f[x]f[y],其中Gcd(x, y)==1
③如果②中没有条件Gcd(x, y)==1,都满足f[xy] = f[x]f[y]那么f[x]为完全积性函数
④积性函数的前缀和也是积性函数
其中莫比乌斯函数u(n)是积性函数
莫比乌斯反演的证明:
第一个等号很好证明,直接将F()的公式代入就好了
第二个等号:这个式子很显然d和d'都是n的约数,d*d' = d'*d = n可以直接交换d和d'而不影响,
第三个等号:但d'!=n时由u(n)函数性质①可得整个式子值为0,当d'==n时整个式子右半部分为1,左半部分为f(n)
那么如何求出u(n)呢?
具体代码如下,类似于质数的预处理,预处理前n项的复杂度<
int cnt, pri[100025], flag[100025] = {1,1}, mu[100005] = {0,1};
for(i=2;i<=100005;i++)
{
if(flag[i]==0) //如果i是质数,显然mu[i]=-1
{
pri[++cnt] = i;
mu[i] = -1;
}
for(j=1;j<=cnt&&i*pri[j]<=100005;j++)
{
flag[i*pri[j]] = 1;
if(i%pri[j]==0) //(令x=pri[j]),如果i是质因子x的倍数,那么mu[i*x]一定为0
{
mu[i*pri[j]] = 0;
break; //直接break,既然i%pri[j]==0,那么i*pri[j+1]==i/pri[i]*(pri[i]*pri[j+1])后面也一定会遍历到
}
mu[i*pri[j]] = -mu[i];
}
}1101: [POI2007]Zap
Time Limit: 10 Sec Memory Limit: 162 MBSubmit: 2642 Solved: 1111
[ Submit][ Status][ Discuss]
Description
Input
第一行包含一个正整数n,表示一共有n组询问。(1<=n<= 50000)接下来n行,每行表示一个询问,每行三个正整数,分别为a,b,d。(1<=d<=a,b<=50000)
Output
对于每组询问,输出到输出文件zap.out一个正整数,表示满足条件的整数对数。
Sample Input
Sample Output
这题是要求
令c = a/D,d = b/D,那么相当于求
由莫比乌斯函数的性质①可将上式子化为
仔细分析这个式子,可以发现假设对于当前的值p,有t对(x, y)满足p同时是x和y的约数,那么答案就加上u(p)*t
很显然t = (能被p整除的x的个数)*(能被p整除的y的个数)即[c/x]*[d/y]([]表示向下取整)
所以最后答案就为
所以只要枚举p就好了,可这样还是会超时,但因为[c/p]和[d/p]的取值只有2sqrt(c)和2sqrt(d)个,那么可以枚举它们的取值,其中u(p)的求法在上面有写
#include
#include
#include
using namespace std;
int cnt, pri[100025], flag[100025] = {1,1}, mu[100005] = {0,1}, sum[100005];
int Jud(int n, int m)
{
int ans, L, R;
ans = 0;
if(n>m)
swap(n, m);
L = 1;
while(L<=n)
{
R = min(n/(n/L), m/(m/L));
ans += (sum[R]-sum[L-1])*(n/L)*(m/L);
L = R+1;
}
return ans;
}
int main(void)
{
int T, n, m, d, ans, i, j;
for(i=2;i<=100005;i++)
{
if(flag[i]==0)
{
pri[++cnt] = i;
mu[i] = -1;
}
for(j=1;j<=cnt&&i*pri[j]<=100005;j++)
{
flag[i*pri[j]] = 1;
if(i%pri[j]==0)
{
mu[i*pri[j]] = 0;
break;
}
mu[i*pri[j]] = -mu[i];
}
}
for(i=1;i<=100005;i++)
sum[i] = mu[i]+sum[i-1];
scanf("%d", &T);
while(T--)
{
scanf("%d%d%d", &n, &m, &d);
ans = Jud(n/d, m/d);
printf("%d\n", ans);
}
return 0;
}