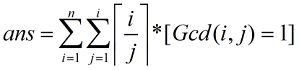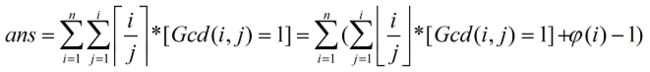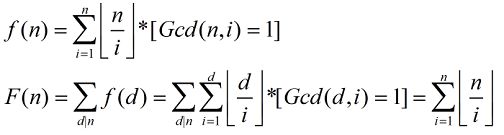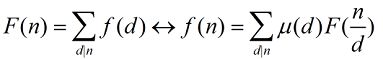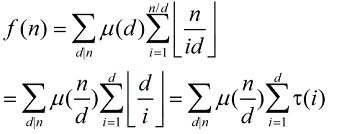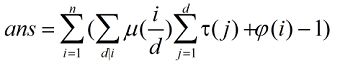HDU 6134 && 2017 多校训练：Battlestation Operational（莫比乌斯反演+积性函数）

实在太长了直接放题目链接

http://acm.hdu.edu.cn/showproblem.php?pid=6134

这题就是求

考虑当Gcd(i, j)==1时，除了j为1的情况，其它时候i/j一定是小数，所以i/j向上取整相当于向下取整的结果+1

那么有：（其中φ(i)为小于i与i互质的对数，即欧拉函数）

欧拉函数因为是积性函数，可以线性求出，令

为什么上面等式成立？

对于所有的n/i，当n和i不互质时，很显然它们除掉它们的Gcd之后就互质了，而等式左边正是在枚举n的约数

考虑莫比乌斯反演：

那么有：

其中莫比乌斯函数和原公式中的欧拉函数都可以O(n)预处理

这样只要枚举后半部分就可以得出答案了

但很可惜这样复杂度仍然是O(nsqrt(n))的所以比赛中就超时了。。。

卡了好久好久好久。。。

继续想：

上面公式还可以转

其中τ(n)表示n的约数个数，是积性函数也可以线性求出

那么答案有

其中先预处理
τ(n)的前缀和，再预处理u(i)与t(n)前缀和积的前缀和

最后带上欧拉函数再算一波前缀和即可

直接O(1)查询，代码很短，就是做了2个半小时。。。

#include
#include
#define mod 1000000007
#define LL long long
LL cnt[1000005], sum[1000005] = {0,1}, ans[1000005] = {0,1};
int main(void)
{
	LL n, i, j;
	for(i=1;i<=1000000;i++)
	{
		for(j=i;j<=1000000;j+=i)
			cnt[j]++;
	}
	for(i=2;i<=1000000;i++)
		sum[i] = (sum[i-1]+cnt[i-1]+1)%mod;
	for(i=1;i<=1000000;i++)
	{
		for(j=i+i;j<=1000000;j+=i)
			sum[j] = ((sum[j]-sum[i])%mod+mod)%mod;
	}
	for(i=2;i<=1000000;i++)
		ans[i] = (sum[i]+ans[i-1])%mod;
	while(scanf("%lld", &n)!=EOF)
		printf("%lld\n", ans[n]);
	return 0;
}