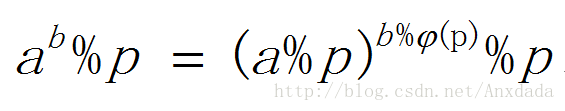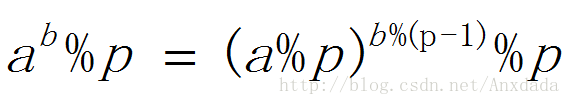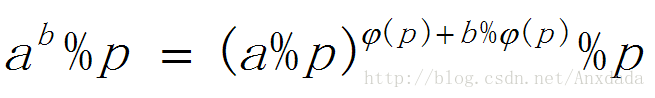欧拉函数 以及 定理相关 兼 板子

//大部分知识都是来源于这片博客的讲解地址

板子理解题
//这可是数论中的巨头啊. 欧拉函数φ(m) 的值是指小于m且与m互质的数的个数. (φ(1) = 1)

所以我们可以通过通式简单的求一求一个数的欧拉函数. (其实也就是一个容斥定理)
代码 ： O(√n)

int phi(int x){  //直接分解质因子求就行了.
    int ans = x;
    for(int i = 2; i*i <= x; i++){
        if(x % i == 0){
            ans = ans / i * (i-1);  //先除是为了防止爆.
            while(x % i == 0) x /= i;
        }
    }
    if(x > 1) ans = ans / x * (x-1); //最后还是一个素数,
    return ans;
}

如果求n个, 明显是很慢的.

所以还有高效一点的, 类似于埃式筛法. n个数(nloglogn).

int phi[maxn];
void Euler()
{
    phi[1] = 1;
    for (int i = 2; i <= maxn; ++i){
        if(!phi[i]){
            for (int j = i; j <= maxn; j += i) {
                if(!phi[j]) phi[j] = j;
                phi[j] = phi[j] / i * (i - 1);
            }
        }
    }
}

xx, 当然还有更快的方法.

不过要用到一下性质.

p为质数 (2，3 定理不会证明, 有兴趣的自己证 )

1. phi(p)=p-1 因为质数p除了1以外的因数只有p，故1至p的整数只有p与p不互质

2. 如果i mod p = 0, 那么 phi(i * p)=phi(i) * p

3. 若i mod p ≠0, 那么 phi( i * p )=phi(i) * ( p-1 )

Code ( 复杂度不会算, 总之更快, 因为上面那道题, 看AC 的time, 还快了不少)

int phi[maxn];
int cnt;
int prime[maxn];
void Euler()
{
    phi[1] = 1; cnt=0;
    for(int i=2;iif(!phi[i]){
            phi[i] = i-1;
            prime[cnt++] = i;
        }
        for(int j=0; j1ll*i*prime[j] < maxn ; j++){
            if( i % prime[j] ) phi[i * prime[j] ] = phi[i] * (prime[j] - 1);
            else{
                phi[ i * prime[j] ] = phi[i] * prime[j];
                break;
            }
        }
    }
}

欧拉定理：
若n,a为正整数，且n,a互质，即gcd(a,n) = 1，则
a^φ(n) ≡ 1 (mod n)

提一下 ：
a^b % p 不等价 (a%p)^(b%p) % p

因为

a^φ(p) ≡ 1 (mod p)

所以

a^b % p = (a%p)^(b%φ(p)) % p

（欧拉函数前提是a和p互质）

如果p是质数（即费马小定理 其实跟 欧拉定理 相同的）

不过数论大佬说又有公式可以摆脱a和p互质的限制
简称为 超欧拉取模进化公式