QSplat：基于点绘制的图形学开山之作

点作为基本的图形绘制元素已经有很长的历史了。早在1974年，Catmull注意到任何几何剖分最终都将显示为一个个离散点。不幸的是点作为基本图形元素在很长一段时间内不受重视，尽管很多系统都将其集成到应用程序界面(API)中。随后Reeves在1983年提出在计算机图形绘制时用3D离散采样点——粒子——作为基本绘制元素。一个粒子是三维欧氏空间内的一个点，附属一些如颜色、密度、光照反射系数等附加信息。粒子系统的最大的优点在于简便快捷的绘制：将每个粒子投影到屏幕上，利用 Z缓冲消隐，并用粒子的颜色给相应像素着色。粒子系统主要应用于一些用传统造型方法很难表示和绘制的自然场景：如火焰与爆炸场面，流水与瀑布。 Levoy与Wihtted在1985年首先提出将点作为基本绘制元素的思想。他们分析出复杂物体用连续的扫描线方法绘制时的缺陷，并指出点虽然简单却足以表示任何物体：只要三维点云足够致密，将一个个点投影到屏幕上后仍然能得到逼真的显示效果。其核心思想是在绘制前将任何物体转化成一系列离散点表示并用一个新的通用算法绘制。他们用圆形 splat 来绘制点，并设定splat的最小尺寸为一个象素以保证绘制质量，同时采用A缓冲技术进行反走样，论文中还详细地考虑了纹理问题。点的独立性基于点的绘制允许高度的并行处理，离散地表示几何而无需存储任何拓扑信息。因此，点云简化了实体表示方法而只保留最重要的信息，尽管无拓扑使得数据结构变得非常简单，它同时会给图形处理带来很大的困难与挑战。高性能绘制、光影计算、各向异性的纹理映射以及进一步的信号处理将是其最大的特点。

1992年Szeliski与Tonneson在Reynolds的工作基础上改进了粒子系统，给原本各向同性的粒子确定了一个法向量，并将这个有向粒子系统应用于模型的表面造型以及交互编辑。每个有向粒子是一个具有局部构架的点，相互间通过远距离引力和近距离斥力发生关联。在绘制有向粒子时他们并没有使用基于点的绘制技术，而是用椭圆来显示粒子，最终实体也是三角化的曲面。1994年Witkin与Heckbert将有向粒子应用于隐式曲面的采样以及交互编辑，并采用同样的绘制方法来显示有向粒子。受基于图像的绘制技术(IBR)的启发，1998年Grossman与 Dally重新开展了点绘制方面的研究工作，其目标是在避免昂贵图形硬件的条件下实时绘制复杂物体。同一时期美国MERL(Mitsubishi Electric Research Laboratories)拓展了surfels(surface elements)的概念。随后，2000年随着Rusinkiewicz等人的Qsplat绘制系统出现, 点绘制技术有了重要突破。

Rusinkiewicz和Levoy给Qsplat系统设计了一种全新的数据结构，高效地压缩了数据并实现了层次LOD控制和基于法向聚类的可见性剔除。在预处理阶段，采样点存储在层次包围球内。在绘制时层次遍历数据结构，根据当前视点视角、屏幕分辨率以及计算条件等情况选择绘制的层次。Qsplat的算法设计允许使用硬件加速绘制，能实时地绘制上亿个点的超大模型。其缺点是没有考虑透明度以及反走样问题，因此绘制质量一般。纯粹用点云来构建场景有其应用缺陷：首先，点云的密集分布造成了大量的数据冗余，极大地消耗了存储、传输以及绘制资源；其次，在当前的几何绘制引擎中，点云在绘制时最终采用三角形或圆面表示，而拓扑关系的缺失使得在视点靠近时无法保证无空洞的绘制效果。因此许多研究者采用多边形与点混合表示场景，这种混合表示方式结合了点与多边形两种表示方式的优点：当绘制元素在屏幕上投影区域很小时用点绘制效率高一些，反过来投影区域较大时用多边形绘制效果更好。

资源下载：http://download.csdn.net/detail/calvinshi/9687606
包含如下文件：
QSplat程序，以及把ply程序转化为QSplat能够读取的qs文件的QSplatMake程序，以及以上两程序的完整C++代码；
QSplat经典论文，以及完整版中文翻译；
关于QSplat的斯坦福原版PPT

三角形作为三维建模中的基本表示元素，在图形学中的应用非常广泛。基于三角形的表面表示需要首先根据物体表面的复杂度进行不规则的采样，然后采用分段线性拟合技术来实现建模过程。这种表示元素不但性质简单，而且可以很有效的表示物体表面的几何属性。同时，在目前的硬件发展中也得到了直接的支持。然而，随着可获取采样点数目的飞速增长，三角化网格的点云数据在实施绘制显示时，会消耗大量的空间和时间。而Qsplat（基于多分辨率处理大规模网格的点绘制系统）数据结构大大的压缩了三角网格点云数据的数据量，这对于大量的数据绘制显示是非常有利的。

图像采集设备将采集的物体点云数据以文本形式存放，例如用软件imageware将数据进行预处理，也就是将点云数据构造成三维网格ply数据文件。也可以采用读入ascii或二进制文件，输出ply文件的方法，参见

http://blog.csdn.net/calvinshi/article/details/53229485

接着要设计ply数据文件与Qsplat数据文件的转换，即对Qsplat数据结构进行设计→设计读取ply数据的函数，并将数据存储在与Qsplat相对应的数据节点中→将读取得的数据进行处理，使数据符合Qsplat的数据格式→建立QS树的算法，并将形成的QS文件输出。

通过调整以及整合扫描的点云数据产生三角网格，它可以通过imageware软件处理获得。

在此基础上，在每个节点上放置一个球体，这个球体要足够大使得能够和旁边的球体相接触。

建立了球体后，要对图3-1（b）建立层次结构。Qsplat是通过将不同区域的边界球进行着色来建立层次结构的。

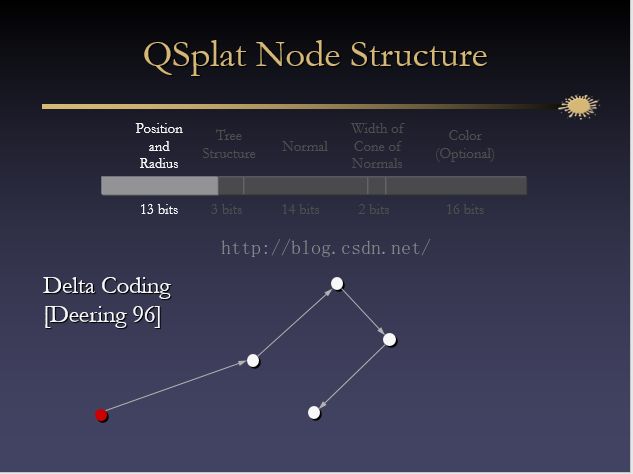
QSplat 用边界球的层次结构作为可见性剔除技术，多细节层次的控制以及绘制。树中每个节点都包含球心位置和半径，泛数和圆锥泛数的宽度，以及颜色（可选）。尽管对程序来说，仅需要一种算法从三角网格中生成这种边界球的层次结构，但是QSplat还能从多边形、体素或者点云模型生成这样的层次结构。这种层次结构作为一种预处理被构造，并被写入到磁盘上。

每个球的球心位置和半径在边界球层次结构上相对于它们的父节点被编码。为了节约空间，这些度量的值定在了13比特。也就是说，球的半径数值范围相对与它父节点是1/13到13/13，球心相对于它父节点（每一个X，Y，Z）的中心的偏移量是它父节点直径的1/13的倍数。量化自顶向下进行，如此孩子节点球的位置和范围相对其父节点的量化的位置而被输入。

每个节点的泛数存储时占用14比特。可表示的泛数对应的点在六面正方体上的52*52的格子上如下（泛数图），并想样本的正规空间上较不一致的弯曲。在绘制时一种查找表被用来对可表示的泛数进行解码。在实践中仅仅使用52 * 52 * 6 = 16224不同的泛数去生成在背景灰暗部分不可见的产物，但是一些条带状的产物在低曲率的广阔区域里高强镜面周围是可见的。

颜色目前存储时占用16个比特， R、G、B分别为5、6、5位。在做泛数运算的时候，颜色增加式的编码能够节约存储空间，但是在运行的时候耗费比较大。

经过实验后，决定给每个节点圆锥泛数宽度仅2比特。四个有代表性的数值对应着面。在典型数据集上，使用量化的圆锥泛数做背面剔除可以裁减掉超过90%的节点。这些节点通过准确的圆锥泛数的宽度被剔除掉。值得注意的是本设计总是保守地去表示圆锥泛数的宽度，所以从不裁减本不该被裁减的几何元素。和泛数以及颜色一样，圆锥泛数的宽度能相对于父节点的宽度而被表示，但是会减慢绘制速度。

高度压缩的数据结构是QSplat方法的一大特点，在该方法中，每个节点的球的位置和半径都是相对于父节点进行编码的，而且将它们离散化为13级离散值，即每个节点的球半径是它的父节点的球半径的1/13至13/13之间的一个值，球心相对于父节点球心的距离是父节点球半径的1/13的倍数。每个节点的法向量也采用离散化表示，用以该点为中心的每个面划分为52x52网格的立方体上的网格点来近似记录向量的方向。圆锥泛数的宽度仅用2位来表示，四个离散值分别表示该圆锥泛数的半顶角的正弦值为1/16、4/16、9/16和16/16的情况。颜色值离散化为16位表示。经过上述压缩表示，最大程度的减少了每个节点所占用的字节数，同时误差控制在可以接受的范围内。这样QSplat在内存和外存中数据表示方式是一样的，绘制时不必先进行解压缩的工作，只需直接将数据调入内存即可，因而进一步加快了绘制的速度。

由于QSplat主要面向大数据量的模型的快速显示，因而，尽管采用了相当大的压缩率，但是每个模型的所需的数据文件仍然很大，尤其是当数据通过网络远程调入时，则很可能会出现数据传输跟不上显示速度的情况。为了解决这一问题，Streaming QSplat[18]方法对QSplat方法进行了修改。因为QSplat可以在递归过程中的任意层次中止，所以Streaming QSplat方法的修改采用了一种非常简单、直接的方法——一旦所需数据尚未传到，则中止递归。这样就可以先行显示一个较粗糙的图像，等数据传到后再逐步求精。

对比ply绘制与QSplat绘制