hdu 3944 DP? （Lucas定理）

DP?

Time Limit: 10000/3000 MS (Java/Others)    Memory Limit: 128000/128000 K (Java/Others)
Total Submission(s): 3095    Accepted Submission(s): 970

Problem Description

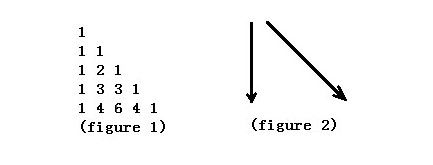
Figure 1 shows the Yang Hui Triangle. We number the row from top to bottom 0,1,2,…and the column from left to right 0,1,2,….If using C(n,k) represents the number of row n, column k. The Yang Hui Triangle has a regular pattern as follows.
C(n,0)=C(n,n)=1 (n ≥ 0)
C(n,k)=C(n-1,k-1)+C(n-1,k) (0 Write a program that calculates the minimum sum of numbers passed on a route that starts at the top and ends at row n, column k. Each step can go either straight down or diagonally down to the right like figure 2.
As the answer may be very large, you only need to output the answer mod p which is a prime.

 

Input

Input to the problem will consists of series of up to 100000 data sets. For each data there is a line contains three integers n, k(0<=k<=n<10^9) p(p<10^4 and p is a prime) . Input is terminated by end-of-file.

 

Output

For every test case, you should output "Case #C: " first, where C indicates the case number and starts at 1.Then output the minimum sum mod p.

 

Sample Input

1 1 2 4 2 7

 

Sample Output

Case #1: 0 Case #2: 5

 

Author

phyxnj@UESTC

 

Source

2011 Multi-University Training Contest 11 - Host by UESTC

 

Recommend

xubiao   |   We have carefully selected several similar problems for you:   3940  3941  3942  3943  3945 

 

Statistic |  Submit |  Discuss | Note

题解：Lucas定理

可能产生答案的只有两种走法

（1）先走最外侧的斜边，然后竖直向下走到达c(n,m)

那么我们会走过m+1个1

然后还需要加入c(m+1，m)+c(m+2,m)+c(m+3,m)+...+c(n,m)

然后我先强行加入c(m+1,m+1),然后可以将c(m+1,m)和c(m+1,m+1)合并成c(m+2,m+1)，然后不断向后合并，最终得到c(n+1,m+1),因为我们加入了c(m+1,m+1)=1所以最终的答案是c(n+1,m+1)+m

（2）先竖直向下，然后走斜边

那么我们会先走过n-m个1

然后还需要加入c(m,0)+c(m+1,1)+c(m+2,2)+...+c(n,m)

c(m,0)=c(m+1,0)替换，然后将c(m+1,0),c(m+1,1)合并得到c(m+2,1)，然后不断向后合并最终得到c(n+1,m)

所以最终的答案是c(n+1,m)+n-m

然后观察后发现，单独的1的个数多的方案最终的结果会更优。

所以当n-m>m,选择方案（2），否则选择方案（1）

#include
#include
#include
#include
#define N 10003
using namespace std;
int jc[2003][N],n,m,p,mp[10003];
int prime[N],pd[N];
void init()
{
   for (int i=2;i<=10000;i++) {
   	if (!pd[i]) prime[++prime[0]]=i,mp[i]=prime[0];
   	for (int j=1;j<=prime[0];j++) {
   		 if (prime[j]*i>10000) break;
   		 pd[prime[j]*i]=1;
   		 if (i%prime[j]==0) break;
	   }
   }
   //cout<>=1;
		base=(base*base)%p;
	}
	return ans;
}
int calc(int n,int m)
{
	if (m>n) return 0;
	return jc[mp[p]][n]*quickpow(jc[mp[p]][m]*jc[mp[p]][n-m]%p,p-2)%p;
}
int lucas(int n,int m)
{
	if (m==0) return 1;
	return calc(n%p,m%p)*lucas(n/p,m/p)%p;
}
int main()
{
	freopen("a.in","r",stdin);
	freopen("my.out","w",stdout);
	int T=0; init();
	while (~scanf("%d%d%d",&n,&m,&p)) {
		T++;
		int a=(lucas(n+1,m+1)-1+m+1)%p;
		int b=(lucas(n+1,m)+n-m)%p;
		//cout<=m) printf("%d\n",b%p);
		else printf("%d\n",a%p);
	}
}