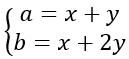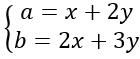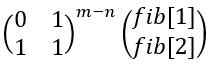LightOJ1052 String Growth[矩阵快速幂]
一串字符串,它只有 a 和 b 组成,假设第 i 个字符串是 abab 那么第 i+1个字符串则为 b(ab)b(ab) 即下一个字符串,是由上一个字符串,通过将 a 变为 b,将 b 变为 ab,得到的。给你第 N 个字符串的跟第 M 个字符串的长度,求出第 K 个字符串的长度,其中,给定的字符串长度会有可能不符合要求,那时请输出Impossible。
题解:
我们假设第 i 个的字符串 a 的个数为 x,b 的个数为 y。
我们看总和的系数 x 的系数是 1 1 2 3 5 y 的系数是 1 2 3 5 8
这显然是非常常见的斐波拉契数列
我们把设定 n < m (如果大于交换一下就好)
打个表,我们可以知道斐波拉契的第46项已经是大于 1e9 的了,而题目给定的长度是个真实长度,并非取模之后的。
那么意味着 n,m 的差值肯定是小于45 (先不说 n,m 是小于45) ,意味着,如果两者如果差值超过了 45 那么必然给定的长度,是错误的。
斐波拉契的起始值 fib[0]=0,fib[1]=1,fib[2]=1。
我们设 第 n 个字符串的 a,b 个数分别为 x,y,x 的系数为 fib[1],y 的系数为 fib[2]
那么第 m 个字符串的 a,b 个数分别为 fib[m-n+1]*x,fib[m-n+2]*y x的系数为fib[m-n+1] y 的系数为fib[m-n+2]
可以用矩阵快速幂或者直接暴力求出第 m 个字符串的 a,b 系数,因为数据差值非常小,所以暴力完全可行。
那么解方程,就可以算出 第 n 个字符串的 a,b 个数,先判断是否可行,即 如果存在 a 或 b 的个数小于0,那么就是Impossible
然而得到这个还不够,首先我们必须先判断了第 n 个字符串是否符合从第 1 个字符串开始变换出来的,即如果出现样例②那样的,第 5 个字符串的长度为 1,这显然是怎么都不可能从第 1 个字符串变出来的。
① n>=45
根据我们上述说过的,第46项斐波拉契数已经是超过了1e9,所以这种情况是Impossible。
② n==1
判断 a 的个数加上 b 的个数是否大于等于0,如果是,那么就直接可以从第 1 项通过算出第 k 项的斐波拉契系数,直接得到答案。否则 Impossible 。
③ n>1 && n<45
因为我们在跟 m 的判断是否符合当中,已经求出了第 n 个字符串的 a,b 个数,那么我们只要知道从第一项开始到第 n 项的 a,b的单独个数的系数。
我们通过刚才上面的公式可以发现 实际上是可以转换成
我们可以发现,只要我们求出 b 的系数即可 因为 f[n-2] = f[n] - f[n-1]。
我们可以发现,第 i 个字符串的 b 的个数的式子里面,y 的系数应该是 fib[i] (从第 1 个字符串开始算起,并且斐波拉契数列从0作为第一项)。 同样用矩阵快速幂求出该系数。
 之后会得到这样两条式子,继续解方程。(
之后会得到这样两条式子,继续解方程。(![]() ,
,![]() 分别代指第 n 个字符串的 a 的个数和 b 的个数,x,y 分别代指第 1 个字符串的 a 的个数和 b 的个数)
分别代指第 n 个字符串的 a 的个数和 b 的个数,x,y 分别代指第 1 个字符串的 a 的个数和 b 的个数)
求出第 1 个字符串的 a,b 的个数,我们可以直接根据这个来求出第 k 个字符串的长度(这次就要一定使用矩阵快速幂了,因为 k 的范围很大)。
#pragma comment(linker, "/STACK:102400000,102400000")
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include ![LightOJ1052 String Growth[矩阵快速幂]_第1张图片](http://img.e-com-net.com/image/info8/284a7a87ef9945dab27c2f98b11cde4e.jpg)
![LightOJ1052 String Growth[矩阵快速幂]_第2张图片](http://img.e-com-net.com/image/info8/ecdba213d47045ba93ff4db3bac60d0d.jpg)

![LightOJ1052 String Growth[矩阵快速幂]_第3张图片](http://img.e-com-net.com/image/info8/7d0227618f9f49c895233a7b1a1b1d6a.jpg)