后缀数组学习笔记

近期学习了后缀数组。
以下是我个人对这一算法的理解。
后缀数组一共有两种算法：倍增法和DC3算法。
前者可以实现 $O(nlo{g}_{2}n)$ 而后者可以实现 $O(n)$ 的时间复杂度来对一个字符串的每个后缀进行排序。
本文介绍的是后缀数组的倍增法，而DC3算法待填。
后缀数组是一种可以将一个字符串的后缀进行排序的算法。

后缀是什么？
后缀是包含原字符串末尾字符的一个子串。
比如串 $\text{ababa}$，它的所有后缀分别是：
$ababa$
$baba$
$aba$
$ba$
$a$
后缀数组可以将这些后缀按照字典序排序。
如上面的所有后缀按字典序从小到大排完序就为：
$a$
$aba$
$ababa$
$ba$
$baba$
拍完序之后我们就可以再继续做一些其他的操作了。
现在重点来了。我们需要怎样才能排序呢？

我们先想：如果我们不会后缀数组呢？该怎么办？
$\mathbb{1.}\ $朴素的做法是我们写一个 $cmp$ 然后 $sort$ 一下就好了。这样做的复杂度是 $O(n^{2}lo{g}_{2}n)$ 的，显然很不优秀。
$\mathbb{2.}\ $ 我们考虑怎么优化上面的做法，$sort$ 的时间复杂度是没办法省去的，所以我们可以在 $cmp$ 上做文章。我们可以用 $hash$ + 二分 的方法来判断两个后缀的字典序， 这样来排序的时间复杂度就是 $O(nlo{g}_2^{2}n)$ 的。
虽然这个思考对后面对后缀数组的理解没什么帮助，但也提供了一个能让我们在考场上写暴力 / 骗分的优秀方法。

回到我们的主题，既然是倍增法的后缀数组，那么我们是如何实现倍增来给后缀数组排序的？
简要来说，倍增法的大致思想就是每次将长度为 $2^x(1<2^x\le n)$ 的已计算出排名的相邻子串合并来计算合并后新子串的排名。
我们记合并前的前半部分的子串为串 $A$， 后半部分的子串为串 $B$， 合并后的子串为串 $C$。

在进行这个操作之前，我们要先处理处长度为 $1$ 的子串（每个字符）的排名。而每次合并之前，$A$ 和 $B$ 的排名是已知的，那么我们要如何求出 $C$ 的排名呢？
我们发现， $A$ 的排名 $a$ 和 $B$ 的排名 $b$ 是互不影响的，且 $a$ 在字符串的比较中比 $b$ 更加重要，因为若两个字符串的前半部分的完全相等，也就是说它们的 $a$ 相等，我们才会去比较它们 $b$ 的大小来判断它们字典序的大小关系。
所以我们就将 $a$ 作为第一关键字， $b$ 作为第二关键字来排序。

如果大家对关键字的概念不够熟悉，看完上面的内容还有点懵，我们就来举一个简单的例子：我们给两位数排序的时候就是以十位为第一关键字，个位为第二关键字来做的。

于是我们给 $C$ 排序时，就可以将它看作一个特殊的两位数 $\overline{ab}$，只要对这个两位数进行排序就可以了。

那么我们用什么排序方法来进行排序呢？
很明显，这个两位数的位数是非常少的，于是对于位数非常少的数进行排序，首先想到的一定是基数排序，这种排序方法可以在 $O(n)$ 的时间复杂度内帮助我们完成这个排序。当然，在第一次对单个字符的排序中，基数排序只在字符集较小的情况下适用。若字符集较大，我们在第一次排序的过程中就选择快速排序，这样会更加优秀。

那么具体该如何实现呢？
我们来看这张图：

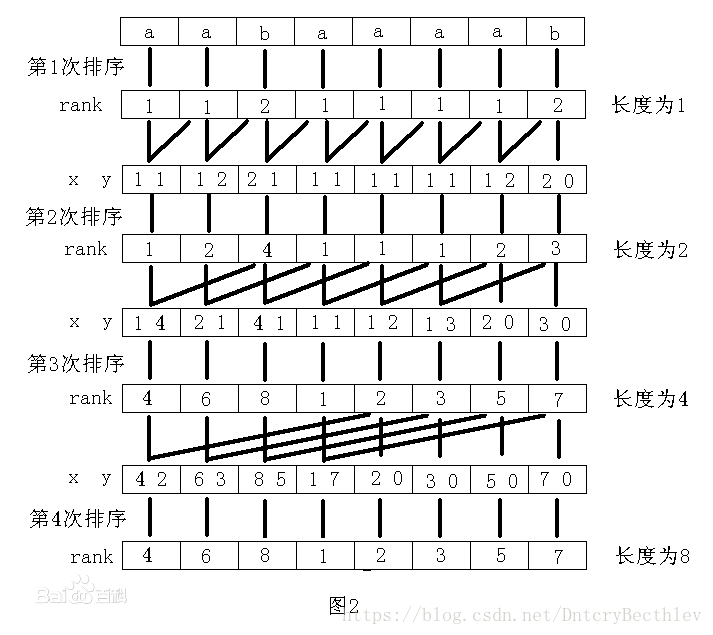
图源百度。
这张图相信大家都见过了，但也许还并不了解这张图的含义，下面是我自己对这张图的理解。
图中的第一行是原字符串的初始状态。
以下每行中，若左边为的文本为 $\text{rank}$，右边文本的长度为 $\text{x}$ ，则第 $i$ 个数字表示从第 $i$ 位开始的，长度为 $\text{x}$ 的字符串的排名。
若左边的文本为 $xy$ 则表示在该次排序过程中，以每个 $C$ 的第一关键字为 $\text{x}$，第二关键字为 $\text{y}$ 来进行排序。在该行内每个格子里的两个数字就是上文所说的 $\overline{ab}$。我们对其进行排序得到下一次的 $\text{rank}$ 。直到从第 $i$ 位开始的字符串的 $\text{rank}$ 都互不相同为止。
我们发现，上图中连接各行之间的有直线和斜线之分的。

若两行之间只有直线就表示下一行是上一行进行排序后的新 $\text{rank}$ 值。
若直线和斜线并存，直线和斜线共同连接下一行的位置即为 $C$ 的起始位置，直线连接上一行的位置为 $A$ 的起始位置，斜线连接的上一行的位置为 $B$ 的起始位置。

我们发现，在直线和斜线共存的两行之间，有一些位置是没有斜线的，这是为什么呢？后半部分没有斜线的原因是在 $C$ 串由两个长度为 $2^x$ 的 $A$，$B$ 串拼接在一起时，$B$ 串为空串，所以 $C$ 的第二关键字为 $0$，不需讨论。而前半部分是因为若以该位置为初始位置的长度为 $2^x$ 的字符串要贡献 $B$ 串时，找不到完整的长度为 $2^x$ 的 $A$ 串与它匹配，无法形成新的 $C$ 串，所以对下一行的排序没有影响。
当我们理解完这张图之后，我们就可以来看具体代码实现了：

我们以 UOJ#35 这道后缀数组模板题为例：

读入一个长度为 $n$ 的由小写英文字母组成的字符串，请把这个字符串的所有非空后缀按字典序从小到大排序，然后按顺序输出后缀的第一个字符在原串中的位置。位置编号为 $1$ 到 $n$。
除此之外为了进一步证明你确实有给后缀排序的超能力，请另外输出 $n-1$ 个整数分别表
示排序后相邻后缀的最长公共前缀的长度。

先来看给后缀排序的这一部分，这一部分用后缀数组实现就可以了:
代码中的 $n$ 为字符串的长度， 初始的 $m$ 为字符集大小。

for(R int i = 1; i <= m; i++) ws[i] = 0;
for(R int i = 1; i <= n; i++) ws[x[i] = Str[i] - 'a' + 1]++;
for(R int i = 2; i <= m; i++) ws[i] += ws[i - 1];
for(R int i = n; i > 0; i--) sa[ws[ x[i] ]--] = i;

这一步是实现了给字符串中的单个字符排序的操作。
在排序的过程中顺便完成了原字符串由字符向数字的转换。
排序原理见计数排序（做一轮的基数排序）。

for(R int j = 1, p; j <= n && p < n; j <<= 1, m = p)

这一行枚举了当前每个串 $A$, $B$ 长度均为 $2^x=j$，不同排名个数为 $p$ 时对字符串的排序过程。
很明显我们知道，当前长度 $j$ 一定要 $\le n$，而当不同排名个数等于 $n$ 时，我们就已经完成对后缀的排序了，每次我们将 $j$ 翻倍， $m$ 变为当前不同排名的个数。因为我们需要排序的一，二关键字是字符串的排名，所以 $m$ 就只要开到字符串当前不同排名的个数就好了。

在排序的过程中，我们把字符串的上一轮第一关键字也就是字符串的排名记在 $x$ 数组中，把作为第二关键字的字符串从大到小记在 $y$ 数组中。
注意了，我们为什么可以直接把作为第二关键字的字符串按照排名记在 $y_i$ 中呢？
这里就要用到后缀数组的一个性质了。

我们观察上面的图，然后可以发现，若当前 $A$，$B$ 长度为 $j$，则从 $n-j+1$ 开始的 $C$ 的第二关键字都为 $0$，将这种情况下 $A$ 的起始位置直接丢进数组，就像这样：
（其中因为 $p$ 暂时没有作用，我们把它作为一个 $tmp$ 来使用）。

p = 0;
for(R int i = n - j + 1; i <= n; i++) y[++p] = i;

然后我们发现，只有位置 $\ge j + 1 $ 的字符串才会作为 $B$ 贡献进这一次排序中的 $C$ 里。所以我们按照上一次排序后的排名从小到大枚举，若当前排名的字符串的位置符合条件，则将与它匹配的 $A$ 的起始位置加入 $y$ 数组， 而 $y$ 依然满足排好序的条件，且结合上面那步， $y$ 中的元素依然是 $n$ 个。实际操作是这样：

for(R int i = 1; i <= m; i++)
	if(sa[i] > j) y[++p] = sa[i];

然后我们要完成的就是对第一关键字的排序了，具体操作和第一步很像，只是将上面的 $x_i$ 变为了 $x_{y_i}$，这样表示将第二关键字排名为 $y_i$ 的字符串按照第一关键字进行排序，代码如下：

for(R int i = 1; i <= m; i++) ws[i] = 0;
for(R int i = 1; i <= n; i++) ws[ x[ y[i] ] ]++;
for(R int i = 2; i <= m; i++) ws[i] += ws[i - 1];
for(R int i = n; i > 0; i--) sa[ws[ x[ y[i] ] ]--] = y[i];

然后我们就是要计算合并之后的 $C$ 的 $\text{rank}$ 值了，这个值我们是要存在 $x$ 数组里的，然而我们在计算时需要用到上一次的 $x$ 值，所以我们就可以用到现在暂时没有用的 $y$ 数组，将原本的 $x$ 数组里的排名放入 $y$ 数组即可，这个操作可以用交换指针来很好的完成。
然后计算当前的 $\text{rank}$ 时，如果基数排序后的两个数的排名相邻，我们就只需要比较它们的第一关键字和第二关键字就可以知道它们是否完全相等了。
代码如下：

//cmp
bool cmp(R int *s, R int a, R int b, R int l)
{
	return a + l <= n && b + l <= n && s[a] == s[b] && s[a + l] == s[b + l];
}
//code
R int *t;
t = x, x = y, y = t;
x[ sa[1] ] = p = 1;
for(R int i = 2; i <= n; i++)
	x[ sa[i] ] = cmp(y, sa[i - 1], sa[i], j) ? p : ++p; 

所以计算排名为 $i$ 的代码如下：

char Str[Maxn];
int ws[Maxn], wa[Maxn], wb[Maxn], sa[Maxn], rank[Maxn], height[Maxn];
bool cmp(R int *s, R int a, R int b, R int l)
{
    return a + l <= n && b + l <= n && s[a] == s[b] && s[a + l] == s[b + l];
}
void SA()
{
    R int *t, *x = wa, *y = wb;
    for(R int i = 1; i <= m; i++) ws[i] = 0;
    for(R int i = 1; i <= n; i++) ws[x[i] = Str[i] - 'a' + 1]++;
    for(R int i = 2; i <= m; i++) ws[i] += ws[i - 1];
    for(R int i = n; i > 0; i--) sa[ws[ x[i] ]--] = i;
    for(R int j = 1, p = 0; p < n && j <= n; j <<= 1, m = p)
    {
        p = 0;
        for(R int i = n - j + 1; i <= n; i++) y[++p] = i;
        for(R int i = 1; i <= n; i++) 
            if(sa[i] > j) y[++p] = sa[i] - j;
        for(R int i = 1; i <= m; i++) ws[i] = 0;
        for(R int i = 1; i <= n; i++) ws[ x[ y[i] ] ]++;
        for(R int i = 2; i <= m; i++) ws[i] += ws[i - 1];
        for(R int i = n; i > 0; i--) sa[ws[ x[ y[i] ] ]--] = y[i];
        t = x, x = y, y = t;
        p = 1, x[ sa[1] ] = 1;
        for(R int i = 2; i <= n; i++)
            x[ sa[i] ] = cmp(y, sa[i - 1], sa[i], j) ? p : ++p;
    }
    return ;
}

以上就是对字符串中的后缀排序的过程。
那么该如何求出相邻后缀的 $LCP$ 呢？
我们发现：
$LCP(i,j)=LCP(j,i)$
$LCP(i,i)=len(sa[i])=n-sa[i]+1$
对于 $i>j$ 的情况，我们可以把它转化成 $i<j$ ，对于 $i=j$ 的情况，我们可以直接算长度，所以我们直接讨论 $i<j$的情况就可以了。
我们设 $height[i]$ 为 $LCP(i,i-1)，(1<i<=n)$，显然 $height[1]=0$
$LCP(i,k)=\min \{height[j]\}(i+1<=j<=k)$
设 $h[i]=height[rank[i]]$，则 $height[i]=h[sa[i]]$;
我们发现 $h[i]>=h[i-1]-1$
这样就可以直接做了。

	for(R int i = 1; i <= n; i++) rank[ sa[i] ] = i;
	for(R int i = 1, k = 0, j; i <= n; height[ rank[i++] ] = k) if(rank[i] > 1)
	{
		k ? k-- : 0;
		for(j = sa[rank[i] - 1]; i + k <= n && j + k <= n && Str[i + k] == Str[j + k]; k++);
	}

后缀数组模板（UOJ#35）：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

#define R register
#define ll long long
#define db double
#define sqr(_x) (_x) * (_x)
#define Cmax(_a, _b) ((_a) < (_b) ? (_a) = (_b), 1 : 0)
#define Cmin(_a, _b) ((_a) > (_b) ? (_a) = (_b), 1 : 0)
#define Max(_a, _b) ((_a) > (_b) ? (_a) : (_b))
#define Min(_a, _b) ((_a) < (_b) ? (_a) : (_b))
#define Abs(_x) (_x < 0 ? (-(_x)) : (_x))

using namespace std;

namespace Dntcry
{
	inline int read()
	{
		R int a = 0, b = 1; R char c = getchar();
		for(; c < '0' || c > '9'; c = getchar()) (c == '-') ? b = -1 : 0;
		for(; c >= '0' && c <= '9'; c = getchar()) a = (a << 1) + (a << 3) + c - '0';
		return a * b;
	}
	inline ll lread()
	{
		R ll a = 0, b = 1; R char c = getchar();
		for(; c < '0' || c > '9'; c = getchar()) (c == '-') ? b = -1 : 0;
		for(; c >= '0' && c <= '9'; c = getchar()) a = (a << 1) + (a << 3) + c - '0';
		return a * b;
	}
	const int Maxn = 100010;
	int n, m;
	char Str[Maxn];
	int ws[Maxn], wa[Maxn], wb[Maxn], sa[Maxn], rank[Maxn], height[Maxn];
	bool cmp(R int *s, R int a, R int b, R int l)
	{
		return a + l <= n && b + l <= n && s[a] == s[b] && s[a + l] == s[b + l];
	}
	void SA()
	{
		R int *t, *x = wa, *y = wb;
		for(R int i = 1; i <= m; i++) ws[i] = 0;
		for(R int i = 1; i <= n; i++) ws[x[i] = Str[i] - 'a' + 1]++;
		for(R int i = 2; i <= m; i++) ws[i] += ws[i - 1];
		for(R int i = n; i > 0; i--) sa[ws[ x[i] ]--] = i;
		for(R int j = 1, p = 0; p < n && j <= n; j <<= 1, m = p)
		{
			p = 0;
			for(R int i = n - j + 1; i <= n; i++) y[++p] = i;
			for(R int i = 1; i <= n; i++) 
				if(sa[i] > j) y[++p] = sa[i] - j;
			for(R int i = 1; i <= m; i++) ws[i] = 0;
			for(R int i = 1; i <= n; i++) ws[ x[ y[i] ] ]++;
			for(R int i = 2; i <= m; i++) ws[i] += ws[i - 1];
			for(R int i = n; i > 0; i--) sa[ws[ x[ y[i] ] ]--] = y[i];
			t = x, x = y, y = t;
			p = 1, x[ sa[1] ] = 1;
			for(R int i = 2; i <= n; i++)
				x[ sa[i] ] = cmp(y, sa[i - 1], sa[i], j) ? p : ++p;
		}
		return ;
	}
	void Celheight()
	{
		for(R int i = 1; i <= n; i++) rank[ sa[i] ] = i;
		for(R int i = 1, k = 0, j; i <= n; height[ rank[i++] ] = k) if(rank[i] > 1)
		{
			k ? k-- : 0;
			for(j = sa[rank[i] - 1]; i + k <= n && j + k <= n && Str[i + k] == Str[j + k]; k++);
		}
		return ;
	}
	int Main()
	{	
		scanf("%s", Str + 1);
		m = 30;
		n = strlen(Str + 1);
		SA();
		Celheight();
		for(R int i = 1; i <= n; i++) printf("%d ", sa[i]); putchar('\n');
		for(R int i = 2; i <= n; i++) printf("%d ", height[i]); putchar('\n');
		return 0;
	}
}
int main()
{
	return Dntcry :: Main();
}