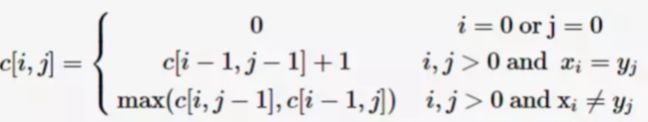动态规划尝试从下面三点寻找解决方案:
- 大问题化成小问题,找出状态方程
- 如果求n,那么n-1如何到n,这就是状态方程
- 利用数组记录1~n的最优结果
- 可以穷举法看规律
一、零钱兑换 leetcode32
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
示例 1:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
详细解读
class Solution:
def coinChange(self, coins, amount):
"""
:type coins: List[int]
:type amount: int
:rtype: int
"""
# if sum(coins) < amount:return -1
dp = [100000000]*(amount+1) # 表示很大的数
dp[0] = 0
for i in range(0,amount+1):
for j in range(len(coins)):
if i>=coins[j]:
dp[i] = min(dp[i-coins[j]]+1,dp[i])
# 这里如果没有赋值的话那么就是找零不了的情况
return dp[amount] if dp[amount]!=100000000 else -1
二、最短路径 leetcode64
class Solution:
def minPathSum(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
m = len(grid)
n = len(grid[0])
for i in range(m):
for j in range(n):
if i == 0 and j == 0:
continue
if i==0 or j == 0:
if i == 0:
grid[0][j]+=grid[0][j-1]
else:
grid[i][0]+=grid[i-1][0]
else:
grid[i][j] = min(grid[i][j-1]+grid[i][j],grid[i-1][j]+grid[i][j])
return grid[m-1][n-1]
三、数字三角形路径和最大 leetcode120
class Solution:
def minimumTotal(self, triangle):
"""
:type triangle: List[List[int]]
:rtype: int
"""
n = len(triangle)
for i in range(n-2, -1, -1):
l = len(triangle[i])
for j in range(l):
triangle[i][j] = min(triangle[i+1][j+1]+triangle[i][j], triangle[i+1][j]+triangle[i][j])
return triangle[0][0]
四、连续子序列和最大 剑指offer
例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组,返回它的最大连续子序列的和。
动态规划思路:
如果以dp[i]表示以第i个数字结尾的子数组最大和,那么我们需要求出max(dp[i]),其中0<=i<=n,递归公式求dp[i]
dp[i]=array[i], i=0 or dp[i-1]<=0
dp[i]=dp[i-1]+array[i], i!=0 or dp[i-1]>0
class Solution:
def FindGreatestSumOfSubArray(self, array):
# write code here
for i in range(len(array)):
if i== 0:continue
if array[i-1] < 0:continue
array[i] = array[i-1]+array[i]
return max(array)
五、最长上升子序列 leetcode300
给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
我们首先用arr[]数组(从0下标开始)存储要求的数列,用longest_num[i]数组来记录以i为结尾的子序列里面包含的最长上升子序列的数字个数。然后用循环控制,从下标为1开始求longest_num,并且记录找到的最大值,即可得到解。在我的程序里面,我还加了一个功能就是把最长上升子序列打印出来,如果存在有多个的话,那么就只打印最后一个。
最后根据下面的DP方程就可以进行求解了:
longest_num[i] = max{longest_num[j] + 1,longest_num[i]} 其中j < i && arr[j] < arr[i]
class Solution:
def lengthOfLIS(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
if nums==[]:
return 0
N = len(nums)
Dp = [1]*N
for i in range(N):
for j in range(i):
if nums[i] > nums[j]:
Dp[i] = max(Dp[i],Dp[j]+1)
return max(Dp)
六、台阶问题
七、小矩形覆盖大矩形
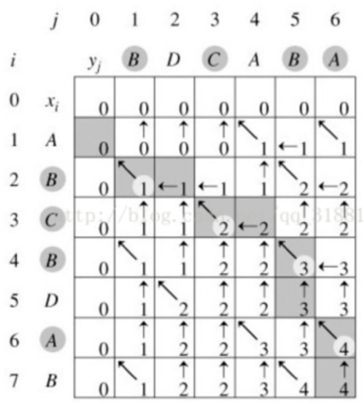
八、最长公共子序列
题目描述:给出两个字符串,找到最长公共子序列(LCS),返回LCS的长度。
样例
给出"ABCD" 和 "EDCA",这个LCS是 "A" (或 D或C),返回1
给出 "ABCD" 和 "EACB",这个LCS是"AC"返回 2
状态方程
def longestCommonSubsequence(str1, str2):
if len(str1) == 0 or len(str2) == 0:return 0
m = len(str1)
n = len(str2)
dp = [ [0 for i in range(n+1)] for i in range(m+1) ]
for i in range(1,m+1):
for j in range(1,n+1):
if str1[i-1] == str2[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j],dp[i][j-1])
return dp[m][n]
九、最长公共子串
样例
给出 "ABCD" 和 "EACB",这个LCS是 "A" (或 B或C),返回1
给出 "BAB" 和 "CABA",这个LCS是 "AB" ,返回2
状态方程
def lcs(str1, str2):
if len(str1) == 0 or len(str2) == 0:return 0
m = len(str1)
n = len(str2)
result = 0
dp = [ [0 for i in range(n+1)] for i in range(m+1) ]
for i in range(1,m+1):
for j in range(1,n+1):
if str1[i-1] == str2[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
result = max(dp[i][j], result);
else:
dp[i][j] = 0
return result
参考
漫画:什么是动态规划?
最长公共子串、最长公共子序列的Java实现与NLP应用