SPLAY树

前言

根据研究表明，90%的访问都是针对10%的元素。提高这90%的访问的效率，就明显改善了对整个访问的效率。
核心思想：把最近访问过的结点提升到根，后续访问的深度将减小。把这种提升结点的操作称为“伸展Splay”。以伸展操作为基础的二叉排序树也就相应称为伸展树（Splay Tree）。

开始

基于前言中十分有用（坑爹 ）的话，于是我们需要用SPLAY树来优化时间，即把刚操作的点引到根下，即SPLAY函数。
但又如何实现这样的操作呢？不妨看看下面的解释。

正文

区别与平衡树（Treap），SPLAY有着更广泛的用途，如线段树的区间修改等等。
现在介绍一下SPLAY树中的一些基本代码。

结构与初始化

struct node{
    node *ch[2],*fa;
    int val,siz;
}tree[MAXN];
node *ncnt,*NIL,*root;
/*
ch：指向该节点的两个儿子的指针
fa：指向该节点父亲的指针
siz：以该节点为根的子树大小
val：该节点的值
tree：指针总容量大小
ncnt：指针计数器
NIL：人工配置的指向空节点的指针
root：指向树的根的指针
*/
void Init(){
    NIL=ncnt=&tree[0];
    NIL->val=-INF;
    root=NIL->ch[0]=NIL->ch[1]=NIL->fa=NIL;
}
/*
NIL与ncnt先指向tree[0]。
即tree[0]为NIL点，tree为内存空间。
root在一来为NIL。
NIL的父亲儿子的是它自己。
*/

插入

node *NewNode(int v){
    node *ret=(++ncnt);
	ret->ch[0]=ret->ch[1]=ret->fa=NIL;
    ret->val=v;ret->siz=1;
    return ret;
}
/*
附上了v值，siz变为了1。
ncnt指向了tree[1],tree[2],tree[3],tree[4]....
*/
void Insert(node *&rt,node *p,int v){
    if(rt==NIL){
        rt=NewNode(v);
        rt->fa=p;
        Splay(rt,NIL);
        return ;
    }
    rt->siz++;
    int d=(rt->val<v);
    Insert(rt->ch[d],rt,v);
}
/*
根据v值不断左左右右（根据二叉查找树的性质）
找到NIL，丢进去。
*/

SPLAY

作为SPLAY树中最核心的函数，SPLAY的基本思想是通过不断不破坏原树秩序的旋转，将一个点旋到另一个点的下面。
而如何不破坏原树秩序的旋转呢？
如图

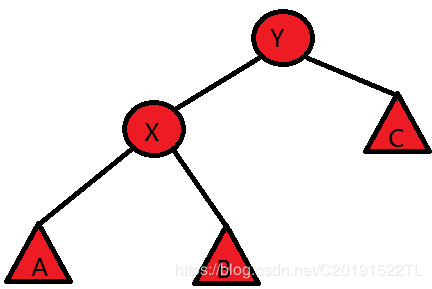
（圆圈为一个点，三角形为一颗子树）
现要将X旋转到Y的上面去，发现A

转化为代码（需要注意许多顺序与细节）：

void PushUP(node *x){
    x->siz=x->ch[0]->siz+x->ch[1]->siz+1;
}//PushUP很随意
void Rotato(node *x){
    node *y=x->fa;
    int d=(x==y->ch[0]);
    x->fa=y->fa;
    if(y->fa!=NIL)y->fa->ch[y==(y->fa->ch[1])]=x;
    y->ch[!d]=x->ch[d];
    if(x->ch[d]!=NIL)x->ch[d]->fa=y;
    x->ch[d]=y;y->fa=x;
    if(root==y)root=x;
    PushUP(y);
}

那么SPLAY函数就可以写了吗？
再由（坑爹的 ）前言可知SPLAY本身也是一种比较迷的算法，为了更加的优化，我们可以在SPLAY时，将单旋优化为双旋，等下再来谈谈双旋为毛更优。
双旋，故名思意，单旋两次。
但旋哪些点才能更优，就很有讲究了，得视情况而定。

第一种情况一字型：

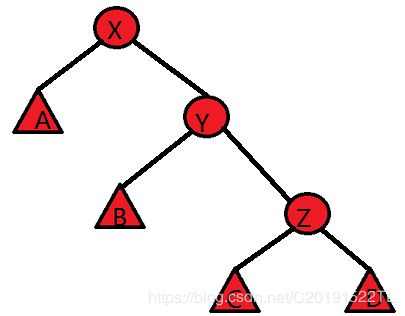
即：将Z选到根如何旋更优。
策略：先旋转父节点，再旋转当前节点。（先Y后Z）

第二种情况之字型：

策略：先旋它自己，再旋它自己。

等下再来谈谈的为毛双旋更优

那么，学习了双旋，SPLAY代码也就出来了。

void Splay(node *x,node *rt){
    node *y,*z;
    while(x->fa!=rt){
        y=x->fa;z=y->fa;
        if(z==rt)Rotato(x);
        else{
            if((x==y->ch[0])^(y==z->ch[0]))
                Rotato(x);
            else Rotato(y);
            Rotato(x);
        }
    }
    PushUP(x);
}

查找系列(+SPLAY优化)

node *Find(node *rt,int v){//第一个值为v的节点
    node *p;
    if(rt==NIL)return NIL;
    if(v==rt->val){
        p=rt->ch[0];
        while(p!=NIL&&p->val==v)
            rt=p,p=p->fa;
        Splay(rt,NIL);
        return rt;
    }
    if(rt->val>v)p=Find(rt->ch[0],v);
    else p=Find(rt->ch[1],v);
    if(p==NIL){p=rt;Splay(rt,NIL);}
    return p;
}
node *FindPrev(node *rt,int v){//v的前驱
    node *p;
    if(rt==NIL)return NIL;
    if(rt->val>=v)
		p=FindPrev(rt->ch[0],v);
	else{
		p=FindPrev(rt->ch[1],v);
		if(p==NIL){p=rt;Splay(p,NIL);}
	}
    return p;
}
node *FindNext(node *rt,int v){//v的后继
    node *p;
    if(rt==NIL)return NIL;
    if(rt->val<=v)
		p=FindNext(rt->ch[1],v);
	else{
		p=FindNext(rt->ch[0],v);
		if(p==NIL){p=rt;Splay(p,NIL);}
	}
    return p;
}
node *FindMax(node *rt){//最大值
    if(rt==NIL)return NIL;
    node *p=rt;
    while(p->ch[1]!=NIL)p=p->ch[1];
    Splay(p,NIL);
    return p;
}
node *FindMin(node *rt){//最小值
    if(rt==NIL)return NIL;
    node *p=rt;
    while(p->ch[0]!=NIL)p=p->ch[0];
    Splay(p,NIL);
    return p;
}
int GetRank(node *rt,int v){//v的排名
    if(rt==NIL)return 1;
    if(rt->val<v)return GetRank(rt->ch[1],v)+(rt->ch[0]->siz)+1;
    else return GetRank(rt->ch[0],v);
}
node *Select(int k,node *f){//排名为k的值
    node *p=root;int lsz;
    while(1){
        lsz=p->ch[0]->siz;
		if(k==lsz+1)break;
		if(lsz>=k)p=p->ch[0];
		else k=k-lsz-1,p=p->ch[1];
    }
	Splay(p,f);
	return p;
}

删点

//无哨兵版本

void Delete(node *rt,int v){
	int k=GetRank(rt,v);
	node *p,*q;
	if(k!=1&&k!=cnt){
		p=Select(k-1,NIL);
		q=Select(k+1,p);
	}
	else{
		if(k==cnt){
			q=Select(k-1,NIL);
			q->ch[1]=NIL;
		}
		else{
			q=Select(2,NIL);
			q->ch[0]=NIL;
		}
		return ;
	}
	q->ch[0]=NIL;
	Splay(q,NIL);
}
/*
将v的前驱SPLAY到根，v的后继SPLAY到根的儿子。
再更掉v的fa的ch，那么v的fa就与v失去了联系，即删除掉了v。
*/

完整代码与版题

版题

#include
#include
using namespace std;
const int MAXN=500005;
const int INF=0X3F3F3F3F;
int n,opt,x,cnt;
struct node{
    node *ch[2],*fa;
    int val,siz;
}tree[MAXN];
node *ncnt,*NIL,*root;
void PushUP(node *x){
    x->siz=x->ch[0]->siz+x->ch[1]->siz+1;
}
void Rotato(node *x){
    node *y=x->fa;
    int d=(x==y->ch[0]);
    x->fa=y->fa;
    if(y->fa!=NIL)y->fa->ch[y==(y->fa->ch[1])]=x;
    y->ch[!d]=x->ch[d];
    if(x->ch[d]!=NIL)x->ch[d]->fa=y;
    x->ch[d]=y;y->fa=x;
    if(root==y)root=x;
    PushUP(y);
}
void Splay(node *x,node *rt){
    node *y,*z;
    while(x->fa!=rt){
        y=x->fa;z=y->fa;
        if(z==rt)Rotato(x);
        else{
            if((x==y->ch[0])^(y==z->ch[0]))
                Rotato(x);
            else Rotato(y);
            Rotato(x);
        }
    }
    PushUP(x);
}
node *Find(node *rt,int v){
    node *p;
    if(rt==NIL)return NIL;
    if(v==rt->val){
        p=rt->ch[0];
        while(p!=NIL&&p->val==v)
            rt=p,p=p->fa;
        Splay(rt,NIL);
        return rt;
    }
    if(rt->val>v)p=Find(rt->ch[0],v);
    else p=Find(rt->ch[1],v);
    if(p==NIL){p=rt;Splay(rt,NIL);}
    return p;
}
node *FindPrev(node *rt,int v){
    node *p;
    if(rt==NIL)return NIL;
    if(rt->val>=v)
		p=FindPrev(rt->ch[0],v);
	else{
		p=FindPrev(rt->ch[1],v);
		if(p==NIL){p=rt;Splay(p,NIL);}
	}
    return p;
}
node *FindNext(node *rt,int v){
    node *p;
    if(rt==NIL)return NIL;
    if(rt->val<=v)
		p=FindNext(rt->ch[1],v);
	else{
		p=FindNext(rt->ch[0],v);
		if(p==NIL){p=rt;Splay(p,NIL);}
	}
    return p;
}
node *FindMax(node *rt){
    if(rt==NIL)return NIL;
    node *p=rt;
    while(p->ch[1]!=NIL)p=p->ch[1];
    Splay(p,NIL);
    return p;
}
node *FindMin(node *rt){
    if(rt==NIL)return NIL;
    node *p=rt;
    while(p->ch[0]!=NIL)p=p->ch[0];
    Splay(p,NIL);
    return p;
}
node *NewNode(int v){
    node *ret=(++ncnt);
	ret->ch[0]=ret->ch[1]=ret->fa=NIL;
    ret->val=v;ret->siz=1;
    return ret;
}
void Insert(node *&rt,node *p,int v){
    if(rt==NIL){
        rt=NewNode(v);
        rt->fa=p;
        Splay(rt,NIL);
        return ;
    }
    rt->siz++;
    int d=(rt->val<v);
    Insert(rt->ch[d],rt,v);
}
void Init(){
    NIL=ncnt=&tree[0];
    NIL->val=-INF;
    root=NIL->ch[0]=NIL->ch[1]=NIL->fa=NIL;
}
int GetRank(node *rt,int v){
    if(rt==NIL)return 1;
    if(rt->val<v)return GetRank(rt->ch[1],v)+(rt->ch[0]->siz)+1;
    else return GetRank(rt->ch[0],v);
}
node *Select(int k,node *f){
    node *p=root;int lsz;
    while(1){
        lsz=p->ch[0]->siz;
		if(k==lsz+1)break;
		if(lsz>=k)p=p->ch[0];
		else k=k-lsz-1,p=p->ch[1];
    }
	Splay(p,f);
	return p;
}
void Delete(node *rt,int v){
	int k=GetRank(rt,v);
	node *p,*q;
	if(k!=1&&k!=cnt){
		p=Select(k-1,NIL);
		q=Select(k+1,p);
	}
	else{
		if(k==cnt){
			q=Select(k-1,NIL);
			q->ch[1]=NIL;
		}
		else{
			q=Select(2,NIL);
			q->ch[0]=NIL;
		}
		return ;
	}
	q->ch[0]=NIL;
	Splay(q,NIL);
}
int main(){
    Init();
    scanf("%d",&n);
    while(n--){
        scanf("%d%d",&opt,&x);
        switch(opt){
            case 1:Insert(root,NIL,x);cnt++;break;
            case 2:Delete(root,x);cnt--;break;
            case 3:printf("%d\n",GetRank(root,x));break;
            case 4:printf("%d\n",Select(x,NIL)->val);break;
            case 5:printf("%d\n",FindPrev(root,x)->val);break;
            case 6:printf("%d\n",FindNext(root,x)->val);break;
        }
    }
}

后记

提取区间操作

假如我们要提取一个区间[a,b]
我们可以将a-1号节点提取到树根，b+1提取到树根的右儿子。
那么a-1即树根的左子树为（1~a-2），
b+1的右子树为（b+2~n），
则根（a-1）的右儿子（b+1）的左子树即为要提取的区间[a,b]。
提取后可以实现线段树的区间操作。

下传与上传

不过多解释。。。
可以自行加些其他要维护的变量。

void PushUP(node *x){ 
    x->siz=x->ch[0]->siz+x->ch[1]->siz+1; 
} 
void PushDown(node *rt){ 
    if(rt==NIL)return ; 
    if(rt->lazy==0)return ; 
    swap(rt->ch[0],rt->ch[1]); 
    if(rt->ch[0]!=NIL)rt->ch[0]->lazy^=1; 
    if(rt->ch[1]!=NIL)rt->ch[1]->lazy^=1;
	rt->lazy=0;
} 

哨兵

在Delete与另外一些操作里，常常需要用到x-1与x+1。
但如果x为第一或最后一个节点时，便会出现RE的情况。
于是我们可以在插入前后分别加一个哨兵节点，以防RE的情况。
但要注意的是哨兵的存在不能影响其他的操作。
（如提取区间时，就提取x与y+2了）

写在后记之后

SPLAY毕竟很迷，有时双旋也过不了。
那么，你就随便SPLAY一些随机的节点吧。
SPLAY总是可以降低树的深度的，不要问我为什么。