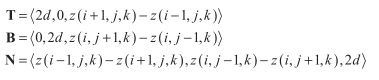[图形学] 实时流体模拟中的数学方法
reference: 《Mathematics for 3D Game Programming and Computer Graphics》
关于这一章节我用OpenGL写了一个可运行的demo,需要的话可以看这里:[OpenGL] 动态的水面模拟
目录
| 1.波动方程 2.近似导数 3.求表面位移 4.实现 5.代码 |
许多游戏里表达的世界里都有被流体表面覆盖的区域。要么是水泊,要么是一桶强酸,或者是熔岩坑,我们想要流体表面能够表现得和物理现实世界一样。我们可以通过模拟流体以波的形式起伏来实现这些效果。在这一章节中,我们介绍著名的波动方程,并将它应用到实时流体表面仿真中。
波动方程
波动方程是一个偏微分方程,它描述了恒张力下一维弦或是二维表面上每个点的运动状态。通过考虑一根端点固定在x轴上的弹性绳,我们可以推导出一维波方程。我们假设该绳子密度均匀分布,并且受到切线方向的恒力F。
![[图形学] 实时流体模拟中的数学方法_第1张图片](http://img.e-com-net.com/image/info8/9d42db633ad343eea7b282d7221b7969.jpg)
让函数z(x,t)表示这根绳子在水平位置x处以及时间t时的垂直位置。当绳子向z方向移动时,绳子上的每个点受到张力并产生加速度。牛顿第二定律指出对于处在x = s和x = s+△x区间的绳子在任一时间t受到的力F(x,t)等于它的质量乘以其加速度a(x,t)。由于绳子的线性密度是![]() ,这一小段绳子的质量是
,这一小段绳子的质量是![]() △x,所以我们有:
△x,所以我们有:
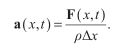
正如下图所示,我们可以把分布在x=s到x=s+△x之间每个点受到的力分解成水平和竖直分量,分别是H(x,t)和V(x,t)。让theta表示绳子在x=s处的切线与x轴之间的夹角。由于张力T沿着切线方向,它的水平分量和竖直分量可以写作:
让![]() 表示在x = s+△x处的切线与x轴之间的夹角。在这一端点的张力水平分量H(s+△x,t)以及竖直分量V(s+△x,t)可以写作:
表示在x = s+△x处的切线与x轴之间的夹角。在这一端点的张力水平分量H(s+△x,t)以及竖直分量V(s+△x,t)可以写作:
对于较细微的运动,我们假设力的水平分量为0,那么这一段的加速度仅在竖直方向上。因此,对于处在x=s和x=s+△x间的一小段绳子而言,有:
![]()
由于函数H与x无关,我们可以直接写成H(t),而不是H(x,t)。
作用于x = s到x = s + △x区域的垂直力将会产生一个由
的z分量给定的加速度。由于垂直的加速度等于位置函数z(x,t)的二次导数,我们有:
两边同乘密度![]() 并且令极限△x趋向于0:
并且令极限△x趋向于0:
方程的右式等价于V的x分量在s处的偏导,所以我们可以把它重写成
使用
中给出的H(t)和V(s,t) 的值,我们可以用H(t)来这样表达V(s,t):
![]()
由于![]() 是绳的切线与x轴的夹角,tan
是绳的切线与x轴的夹角,tan![]() 就等于函数z(x,t)在s处的斜率,因此:
就等于函数z(x,t)在s处的斜率,因此:
我们把这个式子代入(*),得到:
又因为H(t)与x无关,我们写成
对于细微的运动而言,![]() 接近于1,所以我们用张力T来近似表达H(t).令
接近于1,所以我们用张力T来近似表达H(t).令![]() ,我们现在可以得到一维波方程:
,我们现在可以得到一维波方程:
二维波方程可以通过扩展维度得到:
常数c表达了单位时间内的距离,所以我们可以把它表达为速度。关于c,我们有一个没有验证的事实,它实际上是波沿着绳子或者从一个表面上产生的速度。由于波的速度随着介质所受张力增大而增大,并随着介质密度的减小而减小,这将是有意义的。
上式除了表面张力没有考虑到其它的力。因此,表面波的平均振幅不会像现实世界的流体一样衰减。我们可以在等式后面加一个和表面点速度方向相反的粘性阻尼力:
其中,非负的常量![]() 表达了流体的黏度,
表达了流体的黏度,![]() 的值控制了表面波要花多久时间停下来。一个小的
的值控制了表面波要花多久时间停下来。一个小的![]() 值可以让波持续很长一段时间,但是一个大的
值可以让波持续很长一段时间,但是一个大的![]() 值可以让波迅速的消失,正如稠密的油一样。
值可以让波迅速的消失,正如稠密的油一样。
近似导数
考虑黏性阻力的二维波方程可以通过分离变量法解出。但是这个解的形式非常复杂,对于实时模拟而言,它的计算量太大了。因此,我们选择用数值分析的方法来模拟流体表面波的运动。
假设我们的流体表面是由均匀分布在n x m规则网格上的三角形组成的,如下图。设邻接点在x和y方向上的距离均为d,令连续的流体状态计算的时间间隔为t。我们用z(,i,j,k)来表达网格上的一个顶点,其中i,j是满足0<=i 我们利用边界条件推断出处在网格边界上的点位移为0,内部点的位置可以利用前面给出的二维波方程求出,而近似导数可以利用邻接点位移差求出。正如下图所显示的,我们可以通过计算顶点和它x方向的邻接点之间△z和△x的平均比例,来估计顶点(i,j)处沿x轴方向的切线向量。使用这一技术,并且利用△x = d这一事实,我们可以这样表达导数 我们用类似的计算顶点与y方向邻接点的△z与△y的平均比例方法,来定义点(i,j)处的导数 我们可以通过计算某一点当前时间的位移和前一时间位移的差值,以及当前时间和接下来时间的估计位移之间的差值,来定义时间导数 二次导数的估计可以用和一次导数一样的方法,这是通过计算一次导数与空间或时间坐标之一的差值求得的。为了进一步解释这一点,我们考虑在顶点(i,j)处关于x的二次导数。该顶点一阶导数的平均差值 我们把前面求得的一阶导数的值代入这个方程,得到: 除以d我们得到 这个公式要求我们使用与当前点隔了两个点距离的邻近点的位移来计算。幸运的是,我们并未使用邻接点,所以我们可以缩放点(i,j)处的坐标为原来的一半。使用最近的邻接点并且把距离缩减为一半,我们得到了关于x的二阶导数的公式: 类似的关于y以及关于t的二阶导数公式如下: 使用关于t的一阶导数以及我们推导出的三个关于x,y,t的二阶导数,在点(i,j)处有黏性阻力的二维波方程可以被写成这样的形式: 我们想要决定在时间t后的下一个位移z(i,j,k+1),如果我们已经知道当前位移z(i,j,k)以及前一次位移z(i,j,k-1)。z(i,j,k+1)的方程为: 这恰恰是我们想要的。这个公式每一项前面的常量都可以预先计算,每次计算网格顶点时,只剩下三次乘法以及四次加法。 如果波动速率c太快,或者时间间隔t太长,那么我们的迭代方程将会发散到无穷。为了保证位移是有限的,我们需要决定一个确切的坐标值,使得方程在这个值之下保持稳定。为了保证收敛,我们要求从水平表面离开的顶点应当沿着释放时的表面移动。 假设我们有一个nxm的顶点数组,除了坐标为(i0,j0)的顶点,其余顶点都有 z(i,j,0) = 0以及z(i,j,1) = 0。我们令(i0,j0)处的点处在某一位置,使得z(i0,j0,0) = h并且z(i0,j0,1)=h,其中h是一个非0的位移。现在假设在(i0,j0)的点在时间2t时释放,那么计算z(i0,j0,2)的值时,方程的第三项为0,因而我们有: 对于沿着水平表面移动的顶点,它在2t时的位移一定比在t时的位移要小,因此,我们有 把z(i0,j0,2)的值代入,我们得到 所以: 分离c,我们得到 这告诉我们对于任意邻接点间给定距离d以及方程迭代的任意连续时间间隔t,波的速度c一定比这个方程现实的最大值要小。 或者说,我们可以在给定距离d和波速c的轻快下算出最大时间间隔t。然后方程两边同乘 左边的不等式仅仅要求t>0,这是一个自然成立的条件。而右边的不等式可以转化为: 使用二次方程,这个多项式的根为: 由于方程中的二次项系数为正,所以对应的抛物线开口1向上,因此当t分布在根的两边时,多项式是负的。又因为根中根号里的式子大于 使用处在![]() :
:![]() 。和x方向一样,△y = d,所以我们有:
。和x方向一样,△y = d,所以我们有:![]() 。时间间隔为t,所以△z与三△t比例的平均值为:
。时间间隔为t,所以△z与三△t比例的平均值为:![]() 为
为![]() 与△x的比值,这样我们就能定义二次导数:
与△x的比值,这样我们就能定义二次导数:求表面位移
![]()
![]() 并化简:
并化简:![]() ,所以两个根中较小的那个是复数,所以可以被舍去。我们现在可以这样表达时间t的取值范围:
,所以两个根中较小的那个是复数,所以可以被舍去。我们现在可以这样表达时间t的取值范围:![]() 范围外的波速c,或者使用处在落在
范围外的波速c,或者使用处在落在![]() 范围外的时间,都会导致顶点位移的指数爆炸增长。
范围外的时间,都会导致顶点位移的指数爆炸增长。实现
代码
//============================================================================
//
// Listing 15.1
//
// Mathematics for 3D Game Programming and Computer Graphics, 3rd ed.
// By Eric Lengyel
//
// The code in this file may be freely used in any software. It is provided
// as-is, with no warranty of any kind.
//
//============================================================================
#include "VectorClasses.h"
class Fluid
{
private:
long width;
long height;
Vector3D *buffer[2];
long renderBuffer;
Vector3D *normal;
Vector3D *tangent;
float k1, k2, k3;
public:
Fluid(long n, long m, float d, float t, float c, float mu);
~Fluid();
void Evaluate(void);
};
Fluid::Fluid(long n, long m, float d, float t, float c, float mu)
{
width = n;
height = m;
long count = n * m;
buffer[0] = new Vector3D[count];
buffer[1] = new Vector3D[count];
renderBuffer = 0;
normal = new Vector3D[count];
tangent = new Vector3D[count];
// Precompute constants for Equation (15.25).
float f1 = c * c * t * t / (d * d);
float f2 = 1.0F / (mu * t + 2);
k1 = (4.0F - 8.0F * f1) * f2;
k2 = (mu * t - 2) * f2;
k3 = 2.0F * f1 * f2;
// Initialize buffers.
long a = 0;
for (long j = 0; j < m; j++)
{
float y = d * j;
for (long i = 0; i < n; i++)
{
buffer[0][a].Set(d * i, y, 0.0F);
buffer[1][a] = buffer[0][a];
normal[a].Set(0.0F, 0.0F, 2.0F * d);
tangent[a].Set(2.0F * d, 0.0F, 0.0F);
a++;
}
}
}
Fluid::~Fluid()
{
delete[] tangent;
delete[] normal;
delete[] buffer[1];
delete[] buffer[0];
}
void Fluid::Evaluate(void)
{
// Apply Equation (15.25).
for (long j = 1; j < height - 1; j++)
{
const Vector3D *crnt = buffer[renderBuffer] + j * width;
Vector3D *prev = buffer[1 - renderBuffer] + j * width;
for (long i = 1; i < width - 1; i++)
{
prev[i].z = k1 * crnt[i].z + k2 * prev[i].z +
k3 * (crnt[i + 1].z + crnt[i - 1].z +
crnt[i + width].z + crnt[i - width].z);
}
}
// Swap buffers.
renderBuffer = 1 - renderBuffer;
// Calculate normals and tangents.
for (long j = 1; j < height - 1; j++)
{
const Vector3D *next = buffer[renderBuffer] + j * width;
Vector3D *nrml = normal + j * width;
Vector3D *tang = tangent + j * width;
for (long i = 1; i < width - 1; i++)
{
nrml[i].x = next[i - 1].z - next[i + 1].z;
nrml[i].y = next[i - width].z - next[i + width].z;
tang[i].z = next[i + 1].z - next[i - 1].z;
}
}
}
![[图形学] 实时流体模拟中的数学方法_第2张图片](http://img.e-com-net.com/image/info8/4a162122509242ac837ee02c94b046b8.jpg)
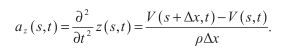
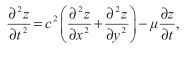
![[图形学] 实时流体模拟中的数学方法_第3张图片](http://img.e-com-net.com/image/info8/994f7b577a47426091d73d2a2099bbac.jpg)
![[图形学] 实时流体模拟中的数学方法_第4张图片](http://img.e-com-net.com/image/info8/a482c3bea31d4511ad556ecc4c80a228.jpg)
![[图形学] 实时流体模拟中的数学方法_第5张图片](http://img.e-com-net.com/image/info8/9752bbeb91f84e4989313776d1183a59.jpg)
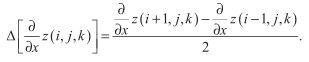

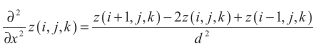
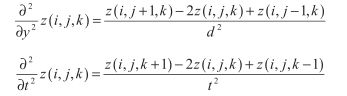
![[图形学] 实时流体模拟中的数学方法_第6张图片](http://img.e-com-net.com/image/info8/f16448f6914545fe9977e10085b20b3b.jpg)
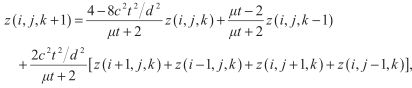
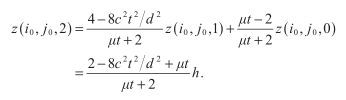
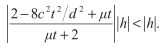
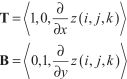
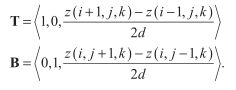
![[图形学] 实时流体模拟中的数学方法_第8张图片](http://img.e-com-net.com/image/info8/206a55ee8b8641e9bfa202d40f568f26.jpg)