第二章 随机变量
随机变量
目标:将实验结果数量化。实验结构有数字型和非数字型。数字型:降雨量、上车人数等。非数字型:晴天/阴天/下雨、化验结果阴性/阳性等。
定义:随机试验样本空间S,如果X=X(e)为定义在S上的实数单值函数,则称X(e)为随机变量。简写为X。
补充:随机变量X(e):S->R 的映射关系。随机变量实质是一个函数。
如果 i≠j ,那么 {X=i}∩{X=j}=ϕ
一般用大写字母X、Y、Z 或者希腊字母 ξ , η 等表示随机变量。
事件表示: A={e:X(e)∈I}={X∈I},I∈R
随机变量的类型:离散型随机变量、连续型随机变量
离散型随机变量
定义:如果随机变量X的取值为有限个,或者可数个,则称X为离散型随机变量。
补充1:换句话说:如果一个函数自变量是有限个,或者可数个,那这个函数就是离散型随机变量。随机变量,是一种映射关系,是函数。
补充2:有限是指知道有多少个,例如一枚硬币扔在地上,结果是正面或者反面,两种结果。可数是指能数的。例如正奇数集{1,3,5,7,…}虽然不知道有多少个,但是是可以一个一个的数的。有些情况是可数且有限个。例如人的年龄是可数且有限的,范围从0,1,2,….200。根据目前的资料,没有人年龄超过200的。那这个个数就是201。
补充3:不可数是无穷集合的一种。一个无穷集合与自然数集合之间不是一一对应的关系,那么这个无穷集合是不可数的(?)。区间[0,1],开始数:
0.34956852…
0.58692….
0.24986….
那么 0.490… 一定是你没有数到的。0.490…是这么来的:该数小数点后的第i位是第i个被数到的数的第i位加1,约定 9+1=0
离散型随机变量的概率分布式律
概率分布律是指随机变量取所有可能取值的情况下,每个取值对应的概率。
| X | x1 | x2 | … | xk | … |
| P | p1 | p2 | … | pk | … |
分布律的性质: pk>=0 ; ∑+∞k=1pk=1
另外一种表示: P(X=xk)=pk,k=1,2,3...
离散型随机变量的包含
0-1分布、二项分布、泊松分布、几何分布都属于离散型随机变量。
0-1分布
定义:若随机变量X可能的取值只有0和1,并且X的概率分布律满足 p0=1−p,p1=p ,其中 0<p<1 ,就称X服从参数为p的0-1分布记为 X∼B(p) 或 X∼0−1(p) 。0-1分布又称为 贝努力分布。
其分布律还可以写为 P(X=K)=pk(1−p)(1−k)
应用
1检查产品质量是否合格
2新生婴儿的性别
3检验种子是否发芽
4考试是否通过
二项分布
关系:如果试验E只有两个可能的结果:A或者 A¯¯¯ ,P(A)=p, 0<p<1 ,将E独立的重复进行n次,想了解n重贝努力试验中A发生的次数的统计规律,就是二项分布。
定义:若X的概率分布律为 P(X=k)=Cknpk(1−p)(n−k),k=0,1,2...,n>=1 , ,0<p<1 ,就称X服从参数n,p的二项分布,记为 X∼B(n,p) 。
泊松分布
如果X的概率分布为 P(X=k)=λke−λk!,k=0,1,2,3..., λ>0 ,就称X服从参数为 λ 的泊松分布,记为 X∼π(λ) 或者 X∼P(λ) 。
根据泰勒展开式 eλ=∑∞k=0λkk!
如果某事件以固定强度 λ ,随机且独立的出现,该事件在单位事件内出现的次数可以看成是泊松分布。
当二项分布的n>10,p<0.1时,二项分布B(n,p)可以用泊松分布P(np)来近似。换句话说:当n远远大于p的时候,泊松分布是二项分布的近似计算公式。
例如:某地区一个月内(单位时间)每200个成年人中会有1个人患上某种疾病(一定概率),设个人是否患病相互独立(随机且独立)。求如果该地某一社区内有1000个成年人,求某月内该社区至少有3人患病的概率。
几何分布
若X的概率分布律为: P(X=K)=p(1−p)k−1 ,k=1,2,3… 称为X服从参数为p的几何分布,记为 X∼Geom(p) 。表示在多重贝努力试验中,试验进行到某一结果第一次出现为止,此时需要的试验次数的分布律。
概率分布函数
定义:随机变量X对任意实数x,称函数F(x)=P(X<=x)为X的概率分布函数,简称分布函数。
补充:任何随机变量都有对应的分布函数
目的:给出随机变量落在某个范围的可能性。
性质:1 0<=F(x)<=1;2 F(x)单调不减;3 F(−∞)=0 , F(+∞)=1 ;4 F(x)是右连续函数,F(x+0) = F(x)。
计算: P(a<X≤b)=P(X≤b)−P(X≤a)=F(b)−F(a)
P(a<X<b)=P(a<X≤b−0)=F(b−0)−F(a)
一般离散型随机变量的分布函数是分段函数。设随机变量X的分布律为P{X=x_k}=p_k,k=1,2,3… X的分布函数为F(x)= ∑xk<=xpk .F(x)在x=x_k处有跳跃,其跳跃值为p_k=P{X=x_k}。

连续型随机变量
定义:随机变量X的取值范围不可数,则称X为连续型随机变量。
分类:均匀分布、指数分布、正态分布。
连续型随机变量的概率密度
定义:对于随机变量X的分布函数F(x),若存在非负的函数f(x),使对于任意实数x有: F(x)=∫+∞−∞f(t)dt 。则称X为连续型随机变量,f(x)为X的概率密度函数,简称概率密度。有时候也写为 fX(x) 。
性质
1 f(x)>=0
2 ∫+∞−∞f(x)dx=1
3 对于任意实数 x1 , x2 , x1<x2 , P(x1<x<x2)=∫x2x1f(t)dt
4 X落在点x附近( x,x+Δx )的概率近似等于 f(x)Δx 。f(x)可以大于1,f(x)的大小表示了X落在x附近的可能性大小,f(x)与F(x)之间是积分与微分的关系。
均匀分布
若随机变量X的概率密度函数为 f(x)=⎧⎩⎨1b−a,x∈(a,b)0,其他 , a<b ,称X服从(a,b)上的均匀分布。记为 X∼U(a,b)

性质:均匀分布具有等可能性。X落入 (a,b) 区间中等长度的任意子区间上是等可能的。
指数分布
若随机变量X的概率密度函数为 f(x)=⎧⎩⎨λe−xλ,x>00,x≤0 ,称X服从 λ 的指数分布。记为 X∼E(λ) 或者 X∼Exp(λ)
分布函数为 F(x)={1−e−λx,x>00,x≤0
性质:指数分布具有无记忆性。 P(X>t0+t|X>t0)=e−λt=P(X>t)
应用
指数分布可以用来表示独立随机事件发生的时间间隔,比如旅客进机场的时间间隔,中文维基百科出现一条新词条的时间间隔。在排队论中,一个顾客接受服务时间的长短也服从指数分布。
正态分布
若随机变量X的概率密度函数为 f(x)=12π−−√σe−(x−μ)22σ2 , −∞<μ<+∞ , σ>0 ,称X服从参数 μ , σ 的正态分布。记为: X∼N(μ,σ2) 。
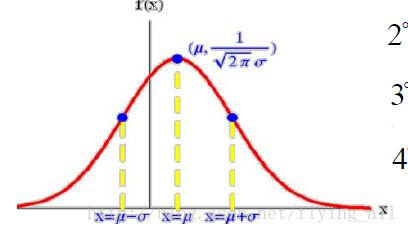
性质
1f(x)关于 x=μ 对称。
2 当 x≤μ 的时候,f(x)严格单调递增。
3 fmax=f(μ)=12π−−√σ
4 lim|x−μ|−>∞f(x)=0
两个参数的含义
1 固定 σ ,f(x)形状不变,移动位置, μ 为位置参数。
2 固定 μ ,f(x)位置不变, σ 小,图形高瘦, σ 大,图形宽胖。称为尺度参数。
应用
1 测量误差。 3σ
2 人的身高、体重
正态分布的计算
方法一:用excel、matlab计算
方法二:数值积分
方法三:转为标准正态分布,查表。
标准正态分布
X∼N(0,1) ,X称为正态分布。
Φ(−z0)=1−Φ(z0)
转换公式
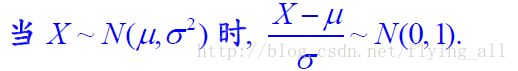

随机变量函数的分布
随机变量函数的分布=函数的函数的分布。已知随机变量X的分布,Y=g(X),g(X)已知,求Y的分布。


一般地,如果 X∼N(μ,σ2) ,如果 Y=ax+b ,则 Y∼N(aμ+b,a2σ2) 。