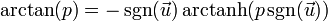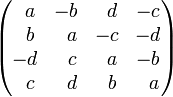四元数的运算规则
转载文章地址：http://blog.csdn.net/chenlanjie842179335/article/details/8039031
四元数是由爱尔兰数学家威廉·卢云·哈密顿在1843年发现的数学概念。四元数的乘法不符合交换律。
明确地说，四元数是复数的不可交换延伸。如把四元数的集合考虑成多维实数空间的话，四元数就代表着一个四维空间，相对于复数为二维空间。
基础
定义
复数是由实数加上元素 i 组成，其中
-
。
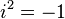相似地，四元数都是由实数加上三个元素 i、j、k 组成，而且它们有如下的关系：
每个四元数都是 1、i、j 和 k 的线性组合，即是四元数一般可表示为
。
要把两个四元数相加只需将相类的系数加起来就可以，就像复数一样。至于乘法则可跟随以下的乘数表：
| × | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | -1 | k | -j |
| j | j | -k | -1 | i |
| k | k | j | -i | -1 |
四元数的单位元的乘法构成了八阶四元群，
。
例子
假设：
那么：
性质
四元数不像实数或复数那样，它的乘法是不可交换的，例如
-
；
-
；
-
。
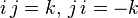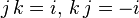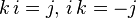四元数是除法环的一个例子。除了没有乘法的交换律外，除法环与域是相类的。特别地，乘法的结合律仍旧存在、非零元素仍有唯一的逆元素。
四元数形成一个在实数上的四维结合代数（事实上是除法代数），并包括复数，但不与复数组成结合代数。四元数（以及实数和复数）都只是有限维的实数结合除法代数。
四元数的不可交换性往往导致一些令人意外的结果，例如四元数的 n-阶多项式能有多于 n 个不同的根。例如方程式 
就有无数多个解。 只要是符合 
的实数，那么 
就是一个解。
一个四元数 
的共轭值定义为：
而它的绝对值则是非负实数，定义为：
注意
，一般状况下不等于
。
四元数的乘逆可以
算得。
透过使用距离函数 
，四元数便可成为同胚于 
的度量空间，并且有连续的算术运算。另外，对于所有四元数
和
皆有 
。 若以绝对值为模，则四元数可组成一实数 巴拿赫空间。
群旋转
如四元数和空间转动条目所释，非零四元数的乘法群在R3的实部为零的部分上的共轭作用可以实现转动。单位四元数（绝对值为1的四元数）若实部为cos(t)，它的共轭作用是一个角度为2t的转动，转轴为虚部的方向。四元数的优点是：
- 表达式无奇点（和例如欧拉角之类的表示相比）
- 比矩阵更简炼（也更快速）
- 单位四元数的对可以表示四维空间中的一个转动。
所有单位四元数的集合组成一个三维球S3和在乘法下的一个群（一个李群）。S3是行列式为1的实正交3×3正交矩阵的群SO(3,R)的双重复盖，因为每两个单位四元数通过上述关系对应于一个转动。群S3和SU(2)同构，SU(2)是行列式为1的复酉2×2矩阵的群。令A为形为a + bi + cj + dk的四元数的集合，其中a, b, c和d或者都是整数或者都是分子为奇数分母为2的有理数。集合A是一个环，并且是一个格。该环中存在24个四元数，而它们是施莱夫利符号为{3,4,3}的正二十四胞体的顶点。
以矩阵表示四元数
有两种方法能以矩阵表示四元数，并以矩阵之加法、乘法应用于四元数之加法、乘法。
第一种是以二阶复数矩阵表示。若 h = a + bi + cj + dk 则它的复数形式为：
这种表示法有如下优点：
- 所有复数 (c = d = 0) 就相应于一个实矩阵。
- 四元数的绝对值的平方就等于矩阵的行列式。
- 四元数的共轭值就等于矩阵的共轭转置。
- 对于单位四元数 (|h| = 1) 而言，这种表示方式给了四维球体和SU(2)之间的一个同型，而后者对于量子力学中的自旋的研究十分重要。（请另见泡利矩阵）
第二种则是以四阶实数矩阵表示：
其中四元数的共轭等于矩阵的转置。
四元数运算
四元数运算在电动力学与广义相对论中有广泛的应用。四元数可以用来取代张量表示。有时候采用带有复数元素之四元数会比较容易，导得结果不为除法代数之形式。然而亦可结合共轭运算以达到相同的运算结果。
此处仅讨论具有实数元素之四元数，并将以两种形式来描述四元数。其中一种是矢量与标量的结合，另一形式两个创建量(constructor)与双矢量(bivector；i、j与k)的结合。
定义两个四元数:
其中
表示矢量
表示矢量
加、乘和一般函数
- 四元数加法：p + q
- 跟 复数 、 矢量 和 矩阵 一样，两个四元数之和需要将不同的元素加起来：
加法遵循实数和复数的所有交换律和结合律。
- 四元数乘法：pq
- 两个四元数之间的非可换乘积通常被 格拉斯曼 称为积，这个积上面已经简单介绍过，它的完整型态是：
由于四元数乘法的非可换性，pq并不等于qp。格拉斯曼积常用在描述许多其他代数函数。qp乘积的矢量部分是:
- 四元数点积： p · q
- 点积也叫做 欧几里得 内积 ，四元数的点积等同于一个四维矢量的 点积 。 点积 的值是p中每个元素的数值与q中相应元素的数值的乘积的和。这是四元数之间的可换积，并返回一个 标量 。
点积可以用格拉斯曼积的形式表示:
这个积对于从四元数分离出一个元素有用。例如，i项可以从p中这样提出来：
- 四元数外积：Outer(p,q)
欧几里得外积并不常用; 然而因为外积和内积的格拉斯曼积形式的相似性.它们总是一同被提及:
- 四元数偶积：Even(p,q)
四元数偶积也不常用，但是它也会被提到，因为它和奇积的相似性。它是纯对称的积；因此，它是完全可交换的。
- 四元数叉积：p × q
四元数叉积也称为奇积。它和矢量叉积等价，并且只返回一个矢量值：
- 四元数转置：p−1
四元数的转置通过p−1p = 1被定义。它定义在上面的定义一节，位于属性之下（注意变量记法的差异）。其建构方式相同于复倒数(complex inverse)之构造：
一个四元数的自身点积是个标量。四元数除以一个标量等效于乘上此标量的倒数，而使四元数的每个元素皆除以此一除数。
- 四元数除法：p−1q
四元数的不可换性导致了 p−1q 和 qp−1的不同。这意味着除非p是一个标量,否则不能使用q/p这一符号。
- 四元数标量部：Scalar(p)
四元数的标量部分可以用前面所述的点积来分离出来：
- 四元数矢量部：Vector(p)
四元数的矢量部分可以用外积提取出来，就象用点积分离标量那样：
- 四元数模：|p|
四元数的绝对值是四元数到原点的距离。
- 四元数符号数：sgn(p)
一复数之符号数乃得出单位圆上，一个方向与原复数相同之复数。四元数的符号数亦产生单位四元数：
- 四元数辐角：arg(p)
辐角函数可找出一4-矢量四元数偏离单位标量(即：1)之角度。此函数输出一个标量角度。
幂和对数
因为四元数有除法，所以幂和对数可以定义。
- 自然幂：
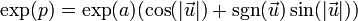
- 自然对数：
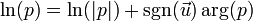
- 幂：
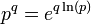
三角函数
- 正弦：
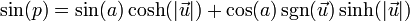
- 余弦：
- 正切：
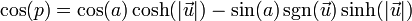
双曲函数
- 双曲正弦:
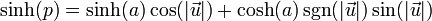
- 双曲余弦:
- 双曲正切:
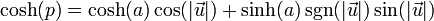
反双曲函数
- 反双曲正弦:
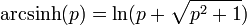
- 反双曲余弦:
- 反双曲正切:
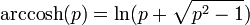
反三角函数
将这些被放到最后，是因为需要先定义四元数中的反双曲三角函数。
- 反正弦函数:
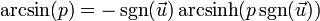
- 反余弦函数:
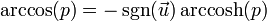
- 反正切函数:
