计算机图形学——光线追踪（RayTracing）算法

前言

最近处于毕设答辩前的空档期，没什么要紧的事情要做，于是空闲之余随意看了下点计算机图形学，学习了一个画3D图形的光线追踪算法，在此简单地分享一下~

一、理论基础

1、三维场景中创建图像

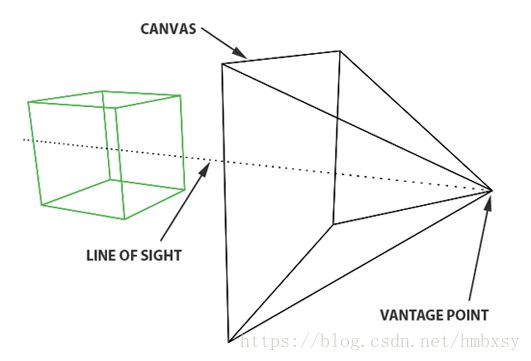
• 第一步：透视投影。这是一个将三维物体的形状投影到图像表面上的几何过程，这一步只需要连接从对象特征到眼睛之间的线，然后在画布上绘制这些投影线与图像平面相交的轮廓。
• 第二步：添加颜色。图像轮廓绘制好之后，给它的骨架添加颜色，这样就完成了三维场景中的图像创建过程。

2、物体的颜色和亮度

• 主要是光线与物体材质相互作用的结果。
• 光由光子（电磁粒子）组成，光子由各种光源发射。当一组光子撞击一个物体时，可能发生三种情况：被吸收，反射或透射。发生这三种情况的光子百分比因材料而异，通常决定了物体在场景中的显现方式。然而，所有材料都有一个共性：入射光子总数总是与反射光子、吸收光子、透射光子的总和相同。
• 白光由“红”、“蓝”、“绿”三种颜色光子组成。当白光照亮红色物体时，光子吸收过程会过滤掉“绿色”和“蓝色”光子。因为物体不吸收“红色”光子，所以它们将被反射，这就是物体呈现红色的原因。
• 我们之所以能够看到物体，是因为物体反射的一些光子向我们传播并击中了我们的眼睛。我们的眼睛由光感受器组成，可以将光信号转换为神经信号，然后我们的大脑能够使用这些信号来辨别不同的阴影和色调。

3、光与物体的关系

• 没有光线，我们都看不到周围的物体。
• 周围环境中没有物体，我们看不到光。

二、光线追踪（RayTracing）算法描述

1、Forward Tracing

在用计算机生成的图像中模拟光与物体相互作用过程之前，我们需要了解一个物理现象。一束光线照射在物体上时，反射的光子中只有少数会到达我们眼睛的表面。想象一下，假设有一个每次只发射一个光子的光源，光子从光源发出并沿着直线路径行进，直至撞击到物体表面，忽略光子的吸收，该光子会以随机的方向反射。如果光子撞击到我们的眼睛表面，则我们会看到光子被反射的点。具体过程如下图所示。

现在从计算机图形的角度来看待这种情况。首先，我们用像素组成的平面代替我们的眼睛。在这种情况下，发射的光子将撞击图形平面上许多像素的一个，并将该点的亮度增加到大于零的值。重复多次直到所有的像素被调整，创建一个计算机生成的图像。这种技术称为前向光线追踪（Forward Tracing），因为我们是沿着光子从光源向观察者的前进的路径。

但是，这种技术在计算机中模拟光子与物体相互作用是不太现实的，因为在实际中反射的光子击中眼睛表面的可能性是非常非常低的，我们必须投射大量的光子才能找到一个能够引起眼睛注意的。此外，我们也不能保证物体的表面被光子完全覆盖，这是这项技术的主要缺点。

换句话说，我们可能不得不让程序一直运行，直到足够的光子喷射到物体的表面上获得精确的显示。这意味着我们要监视正在呈现的图像以决定何时停止应用程序。这在实际生产环境中是不可能的。另外，正如我们将看到的，射线追踪器中最昂贵的任务是找到射线几何交点。从光源产生大量光子不是问题，但是在场景内找到所有的交点将会是非常昂贵的。

2、Backward Tracing

这项技术为前向光线追踪技术的缺陷提供了一个方便的解决方案。由于我们的模拟不能像自然一样快速完美，所以我们必须妥协，并追踪从眼睛进入到场景中的光线。

光线照到一个物体时，我们可以通过将另一条光线（称为光线或阴影光线）从击中点投射到场景的光线，得到它所接受到的光子数量。这个“光线”有的时候会被另一个物体阻挡，这意味着我们原来的撞击点在阴影中，没有获得任何照明。

三、算法实现

1、基本原理

• 光线追踪算法采用由像素组成的图像。对于图像中的每个像素，它将主光线投射到场景中。该主光线的方向是通过追踪从眼睛到像素中心线获得的。一旦我们确定了主射线的方向，我们就开始检查场景中的每个对象，看它是否与其中的任何一个相交。当发生主射线与多个对象相交的情况时，我们选择交点离眼睛最近的物体。
• 然后，我们从交叉点向光线投射阴影射线。如果这条特定的光线在通往光源的路上不与某个物体相交，那么这个点就被照亮了。

• 如果它与另一个物体相交，则该物体在其上投下阴影。

• 最后，如果我们对每个像素重复这一操作，就可以获得三维场景的二维表示。
  

2、伪代码

光线追踪算法实现的伪代码如下所示：

for (int j = 0; j < imageHeight; ++j) { 
    for (int i = 0; i < imageWidth; ++i) { 
        // compute primary ray direction
        Ray primRay; 
        computePrimRay(i, j, &primRay); 
        // shoot prim ray in the scene and search for intersection
        Normal nHit; 
        float minDist = INFINITY; 
        Object object = NULL; 
        for (int k = 0; k < objects.size(); ++k) { 
            if (Intersect(objects[k], primRay, &pHit, &nHit)) { 
                float distance = Distance(eyePosition, pHit); 
                if (distance < minDistance) { 
                    object = objects[k]; 
                    minDistance = distance; // update min distance 
                } 
            } 
        } 
        if (object != NULL) { 
            // compute illumination
            Ray shadowRay; 
            shadowRay.direction = lightPosition - pHit; 
            bool isShadow = false; 
            for (int k = 0; k < objects.size(); ++k) { 
                if (Intersect(objects[k], shadowRay)) { 
                    isInShadow = true; 
                    break; 
                } 
            } 
        } 
        if (!isInShadow) 
            pixels[i][j] = object->color * light.brightness; 
        else 
            pixels[i][j] = 0; 
    } 
} 

四、加入反射和折射

1、基本原理

在光学中，反射和折射是总所周知的现象。反射和折射分向都是基于相交点处的法线和入射光线（主光线）的方向。为了计算折射方向，我们还需指定材料的折射率。

同样，我们也必须意识到像玻璃球这样的物体同时具有反射性和折射性的事实。我们需要为表面上的给定点计算两者的混合值。反射和折射具体值的混合取决于主光线（或观察方向）和物体的法线和折射率之间的夹角。有一个方程式精确地计算了每个应该如何混合，这个方程被称为菲涅耳方程。

加入反射折射后，进行以下三个步骤：

• 计算反射

为此，我们需要两个项：交点处的法线和主光线的方向。一旦我们获得了反射方向，我们就朝这个方向发射新的光线。我们假设反射光线撞击了红色球体，通过向光线投射阴影射线来找出到达红色球体上的那个点的光线多少。这会得到一种颜色（如果是阴影，则为黑色），然后乘以光强并返回到玻璃球的表面。

• 计算折射

注意，因为光线穿过玻璃球，所以它被认为是透射光线（光线从球体的一侧传播到另一侧）。为了计算透射方向，我们需要在知道击中点的法线，主射线方向和材料的折射率。

当光线进入并离开玻璃物体时，光线的方向会改变。每当介质发生变化时都会发生折射，而且两种介质具有不同的折射率。折射对光线有轻微弯曲的作用。这个过程就是让物体在透视时或在不同折射率的物体上出现偏移的原因。

现在让我们想象一下，当折射的光线离开玻璃球时，它会碰到一个绿色的球体。在那里，我们再次计算绿色球体和折射射线之间交点处的局部照明（通过拍摄阴影射线）。然后，将颜色（如果被遮挡，则为黑色）乘以光强并返回到玻璃球的表面。

• 应用菲涅尔方程

我们需要玻璃球的折射率，主光线的角度，以及击中点的法线。使用点积，菲涅耳方程返回两个混合值。

这种算法的美妙之处在于它是递归的。迄今为止，在我们研究过的情况下，反射光线照射到一个红色的、不透明的球体上，而折射光线照射到一个绿色的、不透明的和漫射的球体上。但是，我们会想象红色和绿色的球体也是玻璃球。为了找到由反射和折射光线返回的颜色，我们必须按照与原始玻璃球一起使用的红色和绿色球体的相同过程。

这是光线追踪算法的一个严重缺陷。想象一下，我们的相机是在一个只有反射面的盒子里。从理论上讲，光线被困住了，并且会持续不断地从箱子的墙壁反弹（或者直到你停止模拟）。出于这个原因，我们必须设置一个任意的限制值，从而防止光线相互作用导致的无限递归。每当光线反射或折射时，其深度都会增加。当光线深度大于最大递归深度时，我们就停止递归过程。

2、伪代码

伪代码如下所示：

// compute reflection color
color reflectionCol = computeReflectionColor(); 
// compute refraction color
color refractionCol = computeRefractionColor(); 
float Kr; // reflection mix value 
float Kt; // refraction mix value 
fresnel(refractiveIndex, normalHit, primaryRayDirection, &Kr, &Kt); 
// mix the two
color glassBallColorAtHit = Kr * reflectionColor + (1-Kr) * refractionColor; 

五、参考文献

英文：http://www.scratchapixel.com/lessons/3d-basic-rendering/introduction-to-ray-tracing

源码：http://www.scratchapixel.com/code.php?id=3&origin=/lessons/3d-basic-rendering/introduction-to-ray-tracing