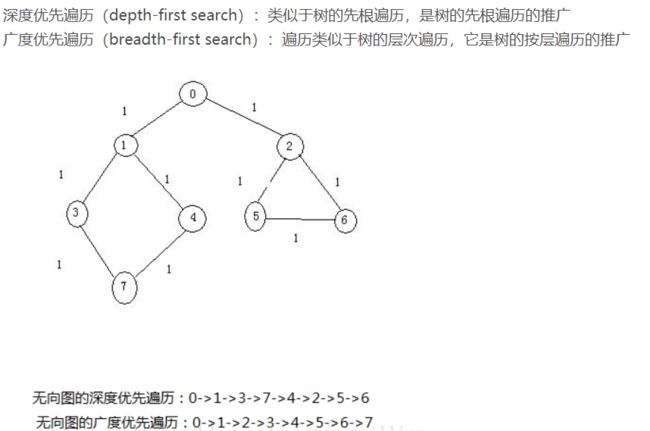
基本概念
1.简单图:1)不存在重复边 。2)不存在顶点到自身的边。
2.完全图:
无向完全图;无向图中任意两点之间都存在边。
有向完全图:有向图中任意两点之间都存在方向向反的两条弧。
3.连通、连通图、连通分量
连通:在无向图中,两顶点有路径存在。
连通图:若图中任意两顶点都连通的图。
连通分量:无向图中的极大连通子图。
存储表示
1.图的邻接矩阵:
#define Maxint 32767 //表示最大值,即∞
#define MVNum 100 //最大顶点数
typedef char VerTexType; //假设顶点的数据类型为字符型
typedef int ArcType; //设边的权值类型为整型
typedef struct {
VerTexType vexs [MVNum];//顶点表
ArcType arcs[MVNum] [MVNum]; //邻接矩阵
int vexnum,arcnum; //图的当前点数和边数
} AMGraph;
2.图的邻接表存储
#define MVNum 100 //最大顶点数
typedef struct ArcNode边结点
{
int adjvex; //该边所指向的顶点的位置
struct ArcNode * nextarc;//指向下一条边的指针
Otherinfo info; //和边相关信息(例如权值)
}ArcNode;
typedef struct VNode//顶点信息
{
VerTexType data;
ArcNode *firstarc; //指向第一条依附该顶点的边的指针
}VNode,AdjList[MVNum]; //AdjList表示邻接表类型
//邻接表
typedef struct
{
AdjList vertices;
int vexnum,arcnum;//图的当前顶点数和边数
}ALGraph;
3.
习题总结
1.在图G中,如果我们必须做两次BFS来访问它的每个顶点,那么G中一定有两个连通的分量
2.Kruskal 算法是通过每步添加一条边及其相连的顶点到一棵树,从而逐步生成最小生成树。(x)
- prim算法是通过每步添加一条边及其相连的顶点到一棵树,从而逐步生成最小生成树;
- Kruskal 算法是维护一个森林,每一步把两棵树合并成一棵。
3.判别以邻接表方式存储的有向图G中是否存在由顶点vi到顶点vj的边(i!=j)
bool has_edge(ALGraph G,VerTexType x,VerTexType y)
{
int i = LocateVex(G,x);//获取顶点下标
int k = LocateVex(G,y);
ArcNode p;
for(p = G.vertices[i].firstarc; p!=NULL;p = p->nextarc)
{
if(p->adjvex == j)//p指向的临界点为j
return true;
}
return false;
}
4.图的BFS生成树的树高比DFS生成树的树小或相等
如只有一个顶点的图,其BFS生成树的树高和DFS生成树的树高相等
对于无权图中 BFS生成树,每个结点到根结点都是最短距离而DFS没有这个限制。
5.如果e是有权无向图G唯一的一条最短边,那么边e一定会在该图的最小生成树上。
6.无向连通图构成的条件是:边数=顶点数-1