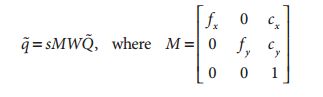相机标定-opencv单应性矩阵实现平面坐标标定（kinect v1）
1、前言
打算通过像素坐标得到对应物体在世界坐标系的三维坐标，但是得到旋转矩阵和平移向量不知道怎么用，内外参乘起来之后，用三维坐标去还原二维坐标，得到的跟实际二维坐标相差十万八千里。
所以最后打算不求内参和外参，直接通过二维平面转换求出对应的单应性矩阵H，然后需要的高度Z再单独通过深度相机得到，所以用了单应性来标定，过程中采集了48个角点，最后的误差x轴在3厘米左右，y轴误差在毫米级，暂时能用，先用着，再去研究其他的方法为啥不行。
2、原理
在计算机视觉中，平面的单应性被定义为一个平面到另外一个平面的投影映射。因此一个二维平面上的点映射到摄像机成像仪上的映射就是平面单应性的例子。如果点Q到成像仪上的点q的映射使用齐次坐标，这种映射可以用矩阵相乘的方式表示。若有一下定义：
则可以将单应性简单的表示为：
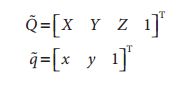
这里引入参数s，它是任意尺度的比例（目的是使得单应性定义到该尺度比例）。通常根据习惯放在H的外面。
H有两部分组成：用于定位观察的物体平面的物理变换和使用摄像机内参数矩阵的投影。
物理变换部分是与观测到的图像平面相关的部分旋转R和部分平移t的影响之和，表示如下
这里R为3*3大小的矩阵，t表示一个一个3维的列矢量。
摄像机内参数矩阵用M表示，那么我们重写单应性如下：
我们知道单应性研究的是一个平面上到另外一个平面的映射，那么上述公式中的Q，就可以简化为平面坐标中的Q’，即我们使Z=0。即物体平面上的点我们用 x,y表示，相机平面上的点，我们也是用二维点表示。我们去掉了Z方向的坐标，那么相对于旋转矩阵R，R可以分解为R=[r1 r2 r3]，那么r3也就不要了，参考下面的推导：
其中H为：
是一个3×3大小的矩阵.
故最终的单应性矩阵可表示如下：
s是相机到物体表面的长度分之一，只是一个比例，我们不需要知道，我的理解就是，我们求出来的是一个H’，而且H’=sH（如果我理解错了，希望指正）。
所以q=H’Q，我们的函数就是求解H’。
Q是物体平面的坐标，q是像素图像的坐标，前者单位我用的是mm，后者是pixel。
我们只需要得到四组对应的点，就可以解的H’，那么为什么是四组，推导如下：
假设p(xi’，yi’)，Q（xi,yi），有下面公式：
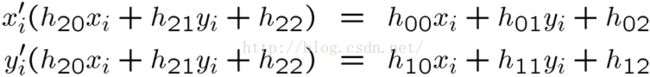
最后我们可以得到如下系数矩阵A：
解其次线性方程组可得Ax=0可得：
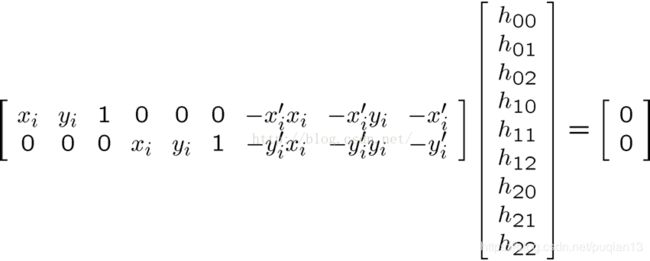
因为是齐次坐标系得到的方程组，H’九个未知数中的一个可以用其他的8个未知数来表示，所以最后我们只需要求解8个未知数（如果理解有错请指正），有上图方程组可以得到一组点可以确定两个方程，所以我们至少需要四组点。
3、代码实现
（1）输入的48组点，来自黑白棋盘的角点检测，真实的场景桌面坐标以第一个角点为（0，0），依次往下计算。
棋盘下载地址：下载链接：
http://wiki.ros.org/camera_calibration/Tutorials/MonocularCalibration?action=AttachFile&do=view&target=check-108.pdf
说明：大小为8x6,可以用A4纸打印出来，square边长为24.5mm，即0.0245m。
（2）代码如下（c++）
using namespace cv;
using namespace std;
int main()
{
//图像尺寸
cv::Size imageSize;
//标定板上每行每列的角点数
cv::Size boardSize = cv::Size(8, 6);
//缓存图像上检测到的角点
std::vector imagePointsBuf;
std::vector imagePointsSeq;
//读入第一张图片并获取图宽高信息
Mat imageInput = cv::imread("qipan/qipan_1.png");
cv::imshow("imageInput", imageInput);
imageSize.width = imageInput.cols;
imageSize.height = imageInput.rows;
std::cout << "imageSize.width = " << imageSize.width << std::endl;
std::cout << "imageSize.height = " << imageSize.height << std::endl;
//提取图片的角点
if (cv::findChessboardCorners(imageInput, boardSize, imagePointsBuf) == 0)
{
//找不到角点
std::cout << "Can not find chessboard corners!" << std::endl;
exit(1000);
}
else
{
//输出48个角点
//std::cout << "imagePointsBuf = " << imagePointsBuf << std::endl;
//int c = imagePointsBuf.size();
//std::cout << c << std::endl;
//转换为灰度图片
Mat viewGray;
cv::cvtColor(imageInput, viewGray, cv::COLOR_BGR2GRAY);
//亚像素精确化 对粗提取的角点进行精确化
cv::find4QuadCornerSubpix(viewGray, imagePointsBuf, cv::Size(5, 5));
//保存亚像素点
//imagePointsSeq.push_back(imagePointsBuf);
std::cout << "二维像素图像点 ：" << imagePointsBuf << std::endl;
//在图像上显示角点位置
//cv::drawChessboardCorners(viewGray, boardSize, imagePointsBuf, true);
//显示图片
//cv::imshow("Camera Calibration", viewGray);
//cv::imwrite("test.jpg", viewGray);
//等待0.5s
//waitKey(500);
}
//计算每张图片上的角点数 54
int cornerNum = boardSize.width * boardSize.height;
std::vector scene_PointSet;
//行数
for (int i = 0; i < 8; i++)
{
//列数
for (int j = 0; j < 6; j++)
{
cv::Point2f realPoint;
//假设标定板放在世界坐标系中z=0的平面上。
realPoint.x = i*24.5;
realPoint.y = j*24.5;
scene_PointSet.push_back(realPoint);
}
}
std::cout << "桌面坐标点 ：" << scene_PointSet << std::endl;
//std::cout << "DAXIAO ：" << scene_PointSet.size() << std::endl;
Mat h = findHomography(scene_PointSet, imagePointsBuf);
//Mat h = findHomography(imagePointsBuf, scene_PointSet);
//Mat warpPerspective_dst;
//warpPerspective(imageInput, warpPerspective_dst, h, imageInput.size());
//imshow("warpPerspective_dst", warpPerspective_dst);
//cv::Mat L = cv::Mat(48, 1, CV_64F, Scalar::all(1));
//Mat N;
//hconcat(scene_PointSet, L, N);
//std::cout << "l ：" < }
单应性矩阵 ：[-0.3867898753811677, -0.1024058969404837, 350.2522938027052; 0.04115322376139761, 0.003417522906883271, 181.9737528555213; -0.000207711216987611, -0.0001663297582563403, 1]