二叉排序树
定义
二叉排序树是一种在结点里存储数据的二叉树。一棵二又排序树或者为空,或者具有下面的性质:
- 其根结点保存着一个数据项(及其关键码)。
- 如果其左子树不空,那么其左子树的所有结点保存的(关键码)值均小于(如果不要求严格小于,也可以是“不大于")根结点保存的(关键码)值。
- 如果其右子树不空,那么其右子树的所有结点保存的(关犍码)值均大于它的根结点保存的(关犍码)值。
- 非空的左子树或右子树也是二叉排序树。
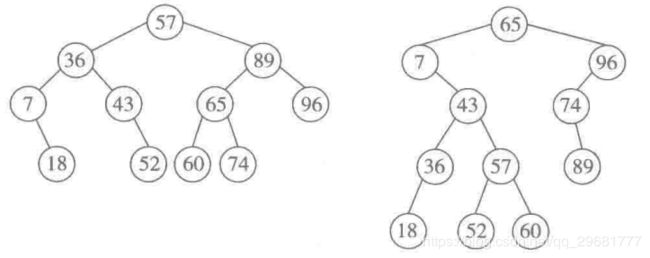
例如,考虑关键码的序列KEY=[36,65,18,7,60,89,43,57,96,52,74]。下图给出了两棵二叉树,其结点里都存储着这组数据。仔细检查不难确认,这两棵二叉树都是二叉排序树。由此实例可见,同一集数据对应的二叉排序树不唯一。但经过中序遍历得到的关键码序列都是一个递增序列。
二叉排序树(字典)类
检索
二叉排序树的一个重要应用是字典的检索。首先定义二叉树节点类和字典元素类。
# 二叉树节点类
class BinTNode:
def __init__(self, dat, left=None, right=None):
self.data = dat
self.left = left
self.right = right
# 字典元素类
class Assoc:
def __init__(self, key, value):
self.key = key
self.value = value
def __lt__(self, other):
return self.key < other.key
def __le__(self, other):
return self.key < other.key or self.key == other.key
def __str__(self):
return "Assoc({0},{1})".format(self.key, self.value)接着定义一个二叉排序树(字典)类,以及它的检索方法。
class DictBinTree:
def __init__(self):
self._root = None
def is_empty(self):
return self._root is None
def search(self, key):
bt = self._root
while bt is not None:
entry = bt.data
if key < entry.key:
bt = bt.left
elif key > entry.key:
bt = bt.right
else:
return entry.value
return None检索过程很清晰,就是根据被检索关键码与当前结点关键码的比较情况,决定是向左走还是向右走。遇到要检索关键码时成功结束,函数返回关键码的关联值;在无路可走时失败结束,函数返回None。
实现二叉排序树字典最关键的操作是数据项的插人和删除,这两个操作通常都要修改树的结构。例如,在做插人操作时,不仅需要保证二叉树的结构完整,将新的数据项加人树中(需要插人新结点),还要保持树中结点数据的正确顺序。
插入
首先考虑字典项的插入。易见,对插人操作的基本要求是能够把新数据项加入字典(二叉排序树)中,并维持二叉树的完整性,包括关键码的顺序要求。为此,就需要找到加人新结点的正确位置,并将新结点正确连接到树中。
查找位置就是用关键码检索,基于检索插人数据的基本算法如下:
- 如果二叉树空,就直接建立一个包括新关键码和关联值的树根节点
- 否则搜索新结点的插入位置,沿子结点关系向下:
遇到应该走向左子树而左子树为空,或者应该走向右子树而右子树为空时,就是找到了新字典项的插入位置,构造新结点并完成实际插入。
遇到结点里的关键码等于被检索关键码,直接替换关联值并结束。
函数的实现如下:
def insert(self, key, value):
bt = self._root
if bt is None:
self._root = BinTNode(Assoc(key, value))
return
while True:
entry = bt.data
if key < entry.key:
if bt.left is None:
bt.left = BinTNode(Assoc(key, value))
return
bt = bt.left
elif key > entry.key:
if bt.right is None:
bt.right = BinTNode(Assoc(key, value))
return
bt = bt.right
else:
bt.data.value = value
return删除
删除的基本想法是先找到需要删除的树结点,将其去除。如果删除破坏了二叉排序树的结构,就在被删结点周围做尽可能小的局部调整。请注意二叉排序树的性质:对其做中序遍历,得到的关键码序列应该是递增的。在分析和检查下面方法的正确性时,可以利用这个性质。
假设已经确定应该删除结点q,它是其父结点的左子结点(为的右子结点的情况类似),这时有两种情况:
1)q是叶结点,这时只需将其父结点到q的引用置为None,删除就完成了。显然,树中剩下的结点仍然构成一棵二叉排序树。
2)q不是叶结点,那么就不能简单删除,需要把q的子树连接到删除q之后的树中,而且要保证关键码的顺序。这时又可以分为两种情况:
(1)如果q没有左子结点,情况如图1中上图所示。这时只需把q的右子树直接改作其父结点p的左子树,得到图1下图的状态。在删除之前,中序遍历序列中先是树中L部分的中序遍历序列,而后是q,再后是q的右子树N的中序序列,再是p和R部分的中序序列。删除之后,除了结点q已经不在,其余部分的顺序不变。如果原来序列中的关键码递增,删除后也一样。
(2)q有左子树,情况如图2上图所示(虽然q可能没有右子树,但可以统一处理)。这时先找到q的左子树的最右结点,设为r,显然它没有右子树。用q的左子节点代替q作为p的左子节点,并将q的右子树作为r的右子树,就得到图2下图的状态。比较删除前和删除后的中序序列,可知这种做法正确。
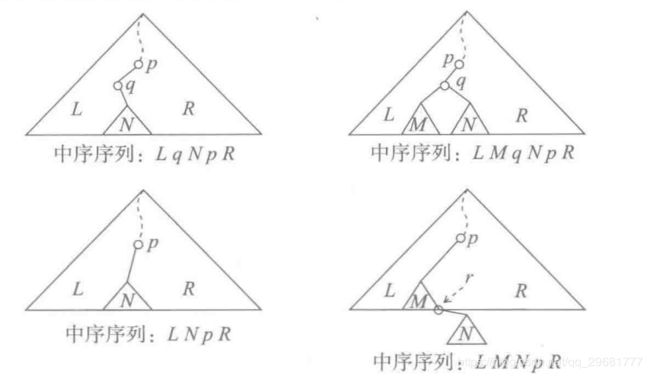 图1 图2
图1 图2
代码如下:
def delete(self, key):
p, q = None, self._root # 维持p为q的父节点
while p is not None and q.data.key != key:
p = q
if key < q.data.key:
q = q.left
else:
q = q.right
if q is None:
return # 树中没有key
if q.left is None: # 如果q没有左子节点
if p is None: # q是根节点,修改_root
self._root = q.right
elif q is p.left: # 根据q和p的关系修改p的子树引用
p.left = q.right
else:
p.right = q.right
return
r = q.left # 找q左子树的最右节点
while r.right is not None:
r = r.right
r.right = q.right
if p is None: # q是根节点,修改_root
self._root = q.left
elif p.left is q:
p.left = q.left
else:
p.right = q.right遍历
对二叉排序树进行中序遍历,由二叉排序树的性质可知,可得到关键码序列的一个递增序列。下面两个函数采用生成器方法,遍历二叉排序树,取出字典的values和entries集合。
def values(self):
t, s = self._root, SStack()
while t is not None or not s.is_empty(): # 中序遍历
while t is not None:
s.push(t)
t = t.left
t = s.pop()
yield t.data.value
t = t.right
def entries(self):
t, s = self._root, SStack()
while t is not None or not s.is_empty(): # 中序遍历
while t is not None:
s.push(t)
t = t.left
t = s.pop()
yield t.data.key, t.data.value
t = t.right测试代码:
dict_tree = DictBinTree()
dict_tree.insert(1, 'a')
dict_tree.insert(3, 'b')
dict_tree.insert(2, 'c')
dict_tree.insert(0, 'd')
dict_tree.insert(0, 'e')
dict_tree.delete(1)
for key, value in dict_tree.entries():
print(key, value)
# 0 e
# 2 c
# 3 b