关于MATLAB的数字信号处理(一)
一、离散时间信号的时域分析
1.序列的产生
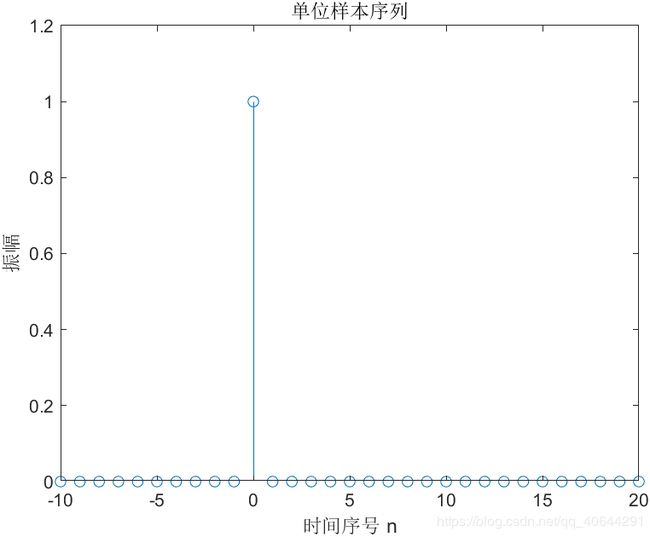
1.1产生绘制一个单位样本序列
用到的基础的MATLAB命令,产生长度为N的单位样本序列u[n]
u=[1 zeros(1,N-1)]
实现代码
![% Program P1_1
% 产生一个单位样本序列
%清除前面的图形
clf;
% 产生一个从 -10 到 20的向量
n = -10:20;
%产生单位样本序列
u = \[zeros(1,10) 1 zeros(1,20)\];
% 绘制单位样本序列
stem(n,u);
xlabel('时间序号 n');ylabel('振幅');
title('单位样本序列');
axis(\[-10 20 0 1.2\]);
1.1.1 对上述的序列延时11个单位,并显示
用到的MATLAB命令
延时M个样本且长度为N的单位样本序列ud[n]
ud=[zeros(1,M) 1 zeros(N-M-1)]
实现代码
% Program P1_1_1
% 产生一个延迟11个单位的单位样本序列
%清除前面的图形
clf;
% 产生一个从 -10 到 20的向量
n = -10:20;
%产生延迟11个单位的单位样本序列
u = [zeros(1,21) 1 zeros(1,9)];
% 绘制单位样本序列
stem(n,u);
xlabel('时间序号 n');ylabel('振幅');
title('延迟11个单位的单位样本序列');
axis([-10 20 0 1.2]);
运行结果
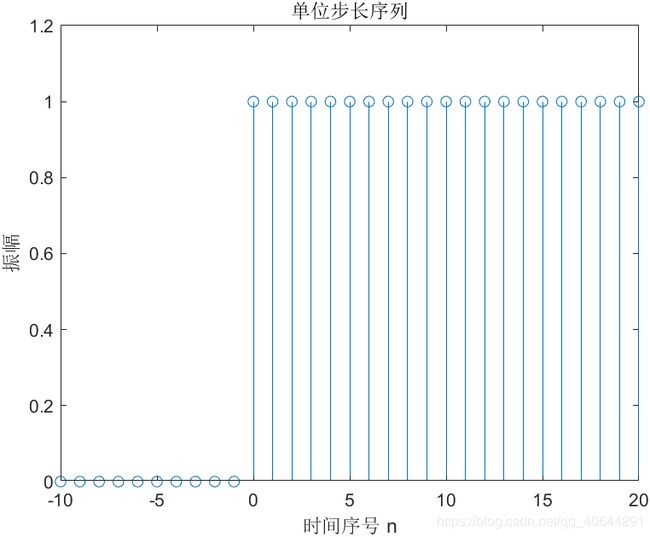
1.1.2 修改程序以产生单位步长序列s[n]
MATLAB 命令产生长度为N的单位阶跃序列 s = [ones(1,N)]
实现代码
% Program P1_1_2
% 产生一个单位步长序列
%清除前面的图形
clf;
% 产生一个从 -10 到 20的向量
n = -10:20;
%产生单位步长序列
s = [zeros(1,10) 1 ones(1,20)];
% 绘制单位步长序列
stem(n,s);
xlabel('时间序号 n');ylabel('振幅');
title('单位步长序列');
axis([-10 20 0 1.2]);
运行结果
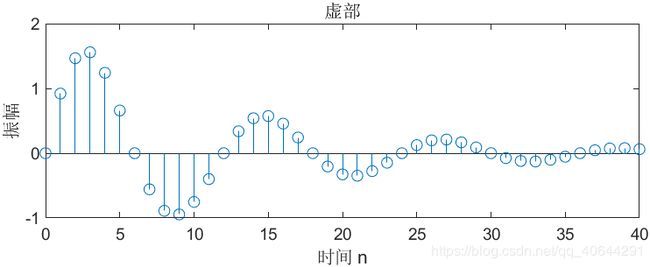
1.2产生一个复指数序列
实验代码
% Program P1_2
% 产生一个复指数序列
clf;
c = -(1/12)+(pi/6)*i;%可控制序列是增长或衰减
K = 2;
n = 0:40;
x = K*exp(c*n);
%分页画图
subplot(2,1,1);
%画出实部的图像
stem(n,real(x));
xlabel('时间 n');ylabel('振幅');
title('实部');
%画出虚部的图像
subplot(2,1,2);
stem(n,imag(x));
xlabel('时间 n');ylabel('振幅');
title('虚部');
实验结果
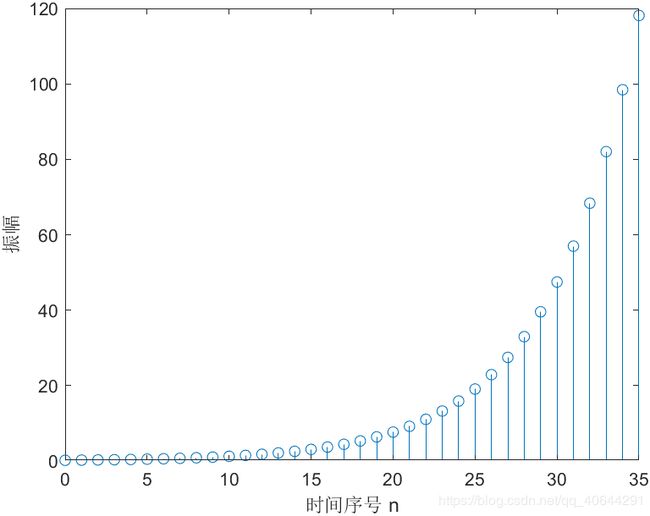
1.3 产生一个实指数序列
实现代码
% Program P1_3
% 产生一个实指数序列
clf;
n = 0:35;
a = 1.2;%控制序列的增长或衰减(值小于1)
K = 0.2;%调整振幅
x = K*a.^n;
stem(n,x);
xlabel('时间序号 n');ylabel('振幅');
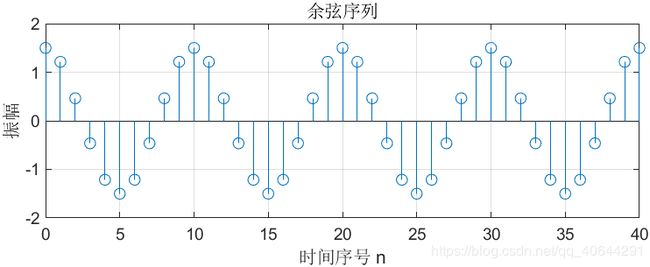
1.4产生一个正弦序列和一个余弦序列
实现代码
% Program P1_4
% 产生一个正弦序列和一个余弦序列
n = 0:40;
f = 0.1; %频率参数
phase = 0; %相位
A = 1.5; %振幅
arg = 2*pi*f*n - phase;
x = A*sin(arg);
y = A*cos(arg);
clf; % 清除旧图形
subplot(2,1,1)
stem(n,x); % 绘制正弦序列
axis([0 40 -2 2]);
grid;
title('正弦序列');
xlabel('时间序号 n');
ylabel('振幅');
subplot(2,1,2)
stem(n,y); % 绘制余弦序列
axis([0 40 -2 2]);
grid;
title('余弦序列');
xlabel('时间序号 n');
ylabel('振幅');
运行结果
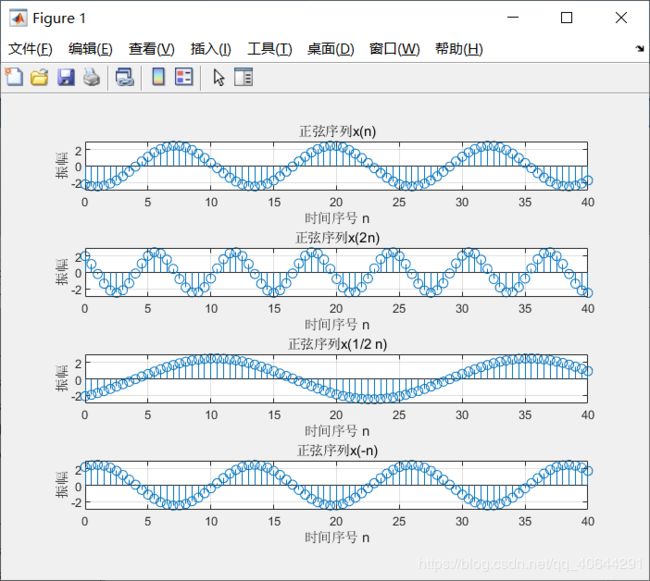
1.5 对一个正弦序列进行压缩和展宽
产生长度为50,频率为0.08,振幅为2.5,相移为90度
实现代码
% Program P1_4
% 产生一个正弦序列
n = 0:0.5:50;
f = 0.08; %频率参数
phase = 90; %相位
A = 2.5; %振幅
arg = 2*pi*f*n - phase;
x = A*sin(arg);
x1 = A*sin(2*arg);%对x进行压缩
x2 = A*sin(1/2*arg);%对x进行展宽
x3 = A*sin(-1*arg);%对x进行反转
clf; % 清除旧图形
subplot(4,1,1);
stem(n,x); % 绘制正弦序列
axis([0 40 -3 3]);
grid;
title('正弦序列x(n)');
xlabel('时间序号 n');
ylabel('振幅');
subplot(4,1,2);
stem(n,x1); % 绘制压缩2倍的正弦序列
axis([0 40 -3 3]);
grid;
title('正弦序列x(2n)');
xlabel('时间序号 n');
ylabel('振幅');
subplot(4,1,3);
stem(n,x2); % 绘制展宽2倍的正弦序列
axis([0 40 -3 3]);
grid;
title('正弦序列x(1/2 n)');
xlabel('时间序号 n');
ylabel('振幅');
subplot(4,1,4);
stem(n,x3); % 绘制反转的正弦序列
axis([0 40 -3 3]);
grid;
title('正弦序列x(-n)');
xlabel('时间序号 n');
ylabel('振幅');
实验结果
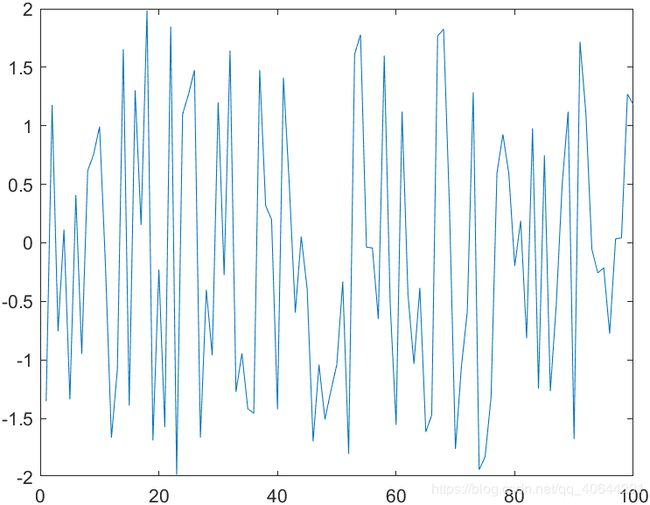
1.6产生一个长度为100的随机信号,该信号在区间[-2,2]上均匀分布
实现代码:
%programer p1_5
%产生一个长度为100的随机信号,该信号在区间[-2,2]上均匀分布
clf;
y=4*rand(1,100)-2; %在[-2,2]上用随机函数rand()产生
plot(y);
运行结果
1.7产生一个显示长度为75的高斯随机信号,该信号正态分布且均值为0,方差为3.
实现代码
%programer p1_5_1
%产生一个显示长度为75的高斯随机信号,该信号正态分布且均值为0,方差为3.
%randn(1,N)函数可以产生长度为N,
%且具有零均值和单位方差的正态分布随机信号
%控制(方差)variance的话,在randn后面乘以一个sqrt(开平方根)
%括号里面就是你的需要的varaince
y1=sqrt(3)*randn(1,75);
plot(y1);
运行结果
1.8 产生并显示五个长度为31的随机正弦信号。
X [ n ] = A ∗ c o s ( ω 0 n + ϕ ) X[n]=A*cos(ω_0 n+ϕ) X[n]=A∗cos(ω0n+ϕ)
其中振幅A和相位ϕ是统计独立的随机变量,振幅在区间0≤A≤4内均匀分布,相位在0≤ ϕ ≤2π内均匀分布
实现代码:
%programer p1_5_2
%编写一个MATLAB程序,以产生并显示五个长度为31的随机正弦信号。
% {X[n]}={A*cos(ω_0 n+ϕ)}
%其中振幅A和相位ϕ是统计独立的随机变量,振幅在区间0≤A≤4内均匀分布,
%相位在0≤ ϕ ≤2π内均匀分布
clf;
w0=2*pi*10;
for k=1:5
%幅度A
A=4*rand(1,31);
%相位phy
phy=2*pi*rand(1,31);
%正弦信号
x=A.*cos(w0*[1:31]+phy);
%分页作图
subplot(5,1,k);
plot(x);
end
2.序列的简单运算
通常处理算法由加法、标量乘法、时间反转、延时或乘积运算等基本运算组合而成
2.1信号平滑
数字信号处理的一个常见例子就是从被加性噪声污染的信号中移除噪声。假定信号s[n]被噪声的d[n]所污染,得到了一个含有噪声的信号x[n]=s[n]+d[n]。我们的目的是对x[n]进行运算,产生一个合理逼近s[n]的信号yn]。因此,对时刻n的样本附近的一些样本求平均,产生输出信号是一种简单有效的方法。
例如,采用三点滑动平均算法(常用的还有五点、十点平均)的表达式如下
y [ n ] = 1 / 3 ( x [ n − 1 ] + x [ n ] + x [ n + 1 ] ) y[n]=1/3(x[n-1]+x[n]+x[n+1]) y[n]=1/3(x[n−1]+x[n]+x[n+1])
加性噪声一般指热噪声、散弹噪声等,它们与信号的关系是相加,不管有没有信号,噪声都存在。
与它存在的另一种噪声为乘性噪声
乘性噪声一般由信道不理想引起,它们与信号的关系是相乘,信号在它在,信号不在它就消失。信道特性随机变化引起的噪声,它主要表现在无线电通信传输信道中,例如,电离层和对流层的随机变化引起信号不反应任何消息含义的随机变化,而构成对信号的干扰。这类噪声只有在信号出现在上述信道中才表现出来,它不会主动对信号形成干扰,因此称之为乘性噪声。
实现代码
% Program P1_6
% 通过平均的信号平滑
clf;
R = 51;
d = 0.8*(rand(R,1) - 0.5); % 产生随机噪声
m = 0:R-1;
s = 2*m.*(0.9.^m); % 产生未污染的信号
x = s + d'; % 产生被噪声污染的信号
subplot(2,1,1);
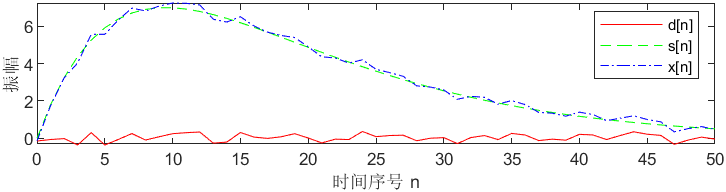
plot(m,d','r-',m,s,'g--',m,x,'b-.');
xlabel('时间序号 n');ylabel('振幅');
legend('d[n] ','s[n] ','x[n] ');%添加图例
%三点滑动平均法
x1 = [0 0 x];x2 = [0 x 0];x3 = [x 0 0];
y = (x1 + x2 + x3)/3;
subplot(2,1,2);
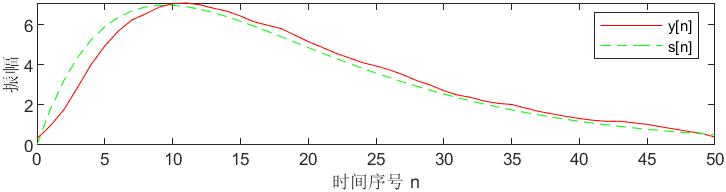
plot(m,y(2:R+1),'r-',m,s,'g--');
legend( 'y[n] ','s[n] ');
xlabel('时间序号 n');ylabel('振幅');
运行结果

尝试五点平均,并观测对比效果
y [ n ] = 1 / 5 ( x [ n − 2 ] + x [ n − 1 ] + x [ n ] + x [ n + 1 ] + x [ n + 2 ] ) y[n]=1/5(x[n-2]+x[n-1]+x[n]+x[n+1]+x[n+2]) y[n]=1/5(x[n−2]+x[n−1]+x[n]+x[n+1]+x[n+2])
实现代码:
% Program P1_6
% 通过平均的信号平滑
clf;
R = 51;
d = 0.8*(rand(R,1) - 0.5); % 产生随机噪声
m = 0:R-1;
s = 2*m.*(0.9.^m); % 产生未污染的信号
x = s + d'; % 产生被噪声污染的信号
subplot(3,1,1);
plot(m,d','r-',m,s,'g--',m,x,'b-.');
xlabel('时间序号 n');ylabel('振幅');
legend('d[n] ','s[n] ','x[n] ');%添加图例
%三点滑动平均法
x1 = [0 0 x];x2 = [0 x 0];x3 = [x 0 0];
y = (x1 + x2 + x3)/3;
subplot(3,1,2);
plot(m,y(2:R+1),'r-',m,s,'g--');
legend( 'y[n] ','s[n] ');
xlabel('时间序号 n');ylabel('振幅');
%尝试五点平均滑动
x1 = [x 0 0 0 0];x2 = [0 x 0 0 0];x3 = [0 0 x 0 0];x4 = [0 0 0 x 0];x5 = [0 0 0 0 x];
y1 = (x1 + x2 + x3 + x4 +x5)/5;
subplot(3,1,3);
plot(m,y1(2:R+1),'r-',m,s,'g--');
legend( 'y[n] ','s[n] ');
xlabel('时间序号 n');ylabel('振幅');
运行结果
对比发现效果最好的是三点滑动平均算法
注意:在语句x=s+**d’**中,若把它改为x=s+d。则出现错误,随机数就并没有加到对应的原始信号上,因为维度不对
2.2复杂信号的产生
更复杂的信号可通过在简单信号上执行基本的运算来产生
例如:振幅信号可用低频调制信号
X L = c o s ( w L n ) X_L=cos(w_L n) XL=cos(wLn)
来调制高频正弦信号
X H [ n ] = c o s ( w L n ) X_H[n]=cos(w_L n) XH[n]=cos(wLn)
得到的信号y(n)为
y ( n ) = A ( 1 + m ⋅ X L [ n ] ) X H ( n ) y(n) =A(1+m·X_L [n])X_H (n) y(n)=A(1+m⋅XL[n])XH(n)
= A ( 1 + m ⋅ c o s ( w L n ) ) c o s ( w L n ) =A(1+m·cos(w_L n))cos(w_L n) =A(1+m⋅cos(wLn))cos(wLn)
其中m为调制指数,用来确保1+m·X_L [n]在所有可能的n的情况下m都是正数。
振幅调制:振幅调制(AM)调制信号m(t)叠加直流后再与载波相乘,则输出的信号就是常规双边带调幅(AM)信号。
AM信号的频谱是由载频分量和上、下两个边带组成(通常称频谱中画斜线的部分为上边带,不画斜线的部分为下边带)。上边带的频谱与原调制信号的频谱结构相同,下边带是上边带的镜像。显然,无论是上边带还是下边带,都含有原调制信号的完整信息。故AM信号是带有载波的双边带信号,它的带宽为基带信号带宽的两倍。
实现代码:
% Program P1_7
% 产生一个振幅调制信号
clf;
n = 0:100;
m = 0.4;
fH = 0.1; %载波频率
fL = 0.01;%调制频率
xH = sin(2*pi*fH*n); %载波信号
xL = sin(2*pi*fL*n);%调制信号
y = (1+m*xL).*xH;%振幅调制信号
stem(n,y);grid;
xlabel('时间序号 n');ylabel('振幅');
运行结果:
3.其他类型的信号
3.1方波和锯齿波信号
实现代码:
% Program P1_8
% 产生一个方波序列和锯齿波序列
clf;
n = 0:30;
m =0:0.5:50;
A=2.5;
y = A*square(n);%产生方波信号
y1= A*sawtooth(m);%产生锯齿波信号
subplot(2,1,1);
stem(n,y);
axis([0 30 -3 3]);
grid;
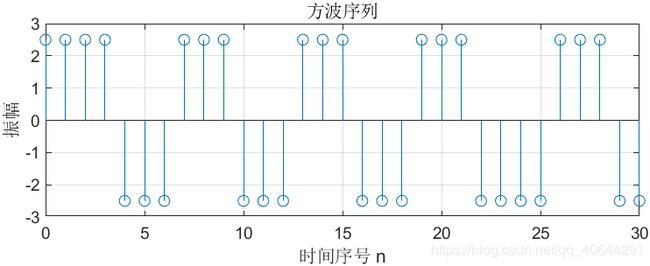
title('方波序列');
xlabel('时间序号 n');ylabel('振幅');
subplot(2,1,2);
stem(m,y1);
axis([0 50 -2.5 2.5]);
grid;
title('锯齿波序列');
xlabel('时间序号 n');ylabel('振幅');