《大话数据结构》笔记:第八章 查找
目录
- 八、查找
- 8.2查找概论
- 8.3顺序表查找
- 8.4有序表查找
- 8.4.1二分查找
- 8.4.2插值查找
- 8.4.3斐波那契查找
- 8.5线性索引查找
- 8.6二叉排序树
- 8.7平衡二叉树(AVL树)
- 8.7.1平衡二叉树实现原理
- 8.8多路查找树(B树)
- 2-3树/2-3-4树
- B树
- 8.9散列表(哈希表)
- 8.10哈希函数的构造
- 8.10.1直接定址法
- 8.10.2数字分析法
- 8.10.3平方取中法
- 8.10.4折叠法
- 8.10.5除留余数法
- 8.10.6随机数法
- 8.11 哈希表冲突
- 8.11.1开放定址法
- 8.11.2再散列函数法
- 8.11.3链地址法
- 8.11.4公共溢出区法
- 8.12哈希表查找
八、查找
查找(Searching)根据给定的某个值,在查找表中确定一个关键字等于给定值的数据元素。
8.2查找概论
关键字(Key)是数据中某个数据项的值,也叫键值。
静态查找表(Static Search Table):只做查找
动态查找表(Dynamic Search Table):查找/插入/删除
8.3顺序表查找
顺序查找(Sequential Searth),又称线性查找。
复杂度O(n),平均O((n+1)/2)
8.4有序表查找
8.4.1二分查找
二分查找(Binary Search),又称折半查找。
前提是有序数组。
时间复杂度O(logn)
这是确定有无特定值,查找最接近的还需要修改。
def binnerFind(lst, value):
#细节1:从0到n-1
start = 0
end = len(lst) - 1
while start <= end:#注意小于等于
#mid = (start + end) // 2
#细节3:防止超出上限,python没必要
mid = start+(end-start)//2
if lst[mid] > value:
#细节2:加一减一
end = mid - 1
elif lst[mid] < value:
start = mid + 1
else:
return mid
return -1
L = [3, 6, 12, 17, 25, 32, 43, 55, 68]
print(binnerFind(L, 43))
8.4.2插值查找
插值查找(Interpolation Search):对二分查找的改进,核心在于插值的计算公式。
适合数据分布均匀的查找。

8.4.3斐波那契查找
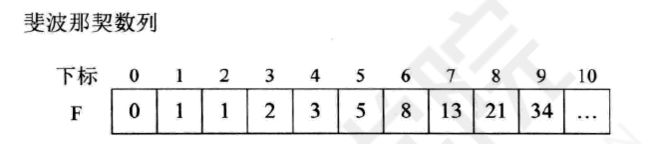
比如范围是0到34,比较第21个数,大于目标值,则下一个范围是0到21,反之为21到34。
#对于大部分数据,比二分效率高些,最坏情况一直在左侧,比二分差。
#而且斐波那契只做加减法,二分是加法和除法,插值是四则运算,斐波那契的加减法应该是最快的。
def fibonacci_sequence(num: int): # 按照待查找数列的大小,动态生成斐波那契数列
a, b = 0, 1
while a <= num-1:
yield a
a, b = b, a + b
yield a
return
def fibonacci_search(a: [], n: int, key: int)->int: # 斐波那契查找
low, high, k = 1, n, 0
F = fibonacci_sequence(n)
dynamic_F = []
for item in F:
dynamic_F.append(item)
while n > dynamic_F[k] - 1:
k += 1
for i in range(n, dynamic_F[k]-1):
a.append(a[n])
while low <= high:
mid = low + dynamic_F[k-1] - 1
if key < a[mid]:
high = mid - 1
k -= 1
elif key > a[mid]:
low = mid + 1
k -= 2
else:
if mid <= n:
return mid
else:
return n
return 0
if __name__ == '__main__':
a = [0, 1, 16, 24, 35, 47, 59, 62, 73, 88, 99]
key = 47
print("key's index is:", fibonacci_search(a, len(a)-1, key))
8.5线性索引查找
稠密索引:每个记录一个索引项,有序
分块索引:块间有序,块内无序。复杂度根号n
倒排索引:比如文章,记录每个单词出现在哪篇文章,通过单词表进行查找文章。
8.6二叉排序树
binary sort tree,又称二叉搜索树。
左子树的值都小于根,右子树都大于根节点。
1.查找。大于当前节点,向右子节点去找,反之左子树。
2.插入。先按查找的顺序,找到最接近的叶节点。根据大小,放在该叶节点的左右子节点。
3.删除。
分三种情况。
3.1叶子节点。
删除该节点
3.2仅有左子树。
删除该节点,其父节点连接到原子节点。
3.3左右子树都有。
理论上是去找中序遍历的上一个节点。
去找中序遍历的下一个节点也可以。
class Node(object):
"""节点定义,包括数据项、左孩子、右孩子"""
def __init__(self, data):
self.data = data
self.lchild = None
self.rchild = None
def Delete(T):
"""删除结点T"""
if T.lchild == None:
"""左子树为空"""
T = T.rchild
elif T.rchild == None:
"""右子树为空"""
T = T.lchild
else:
"""左右子树均不为空"""
p = T
s = T.lchild
while s.rchild:
p = s
s = s.rchild
T.data = s.data
if p != T:
p.rchild = s.lchild
else:
"""此时p = T,说明用的T的左孩子来替代T"""
p.lchild = s.lchild
def DeleteNode(T, key):
if key == T.data:
Delete(T)
elif key > T.data:
DeleteNode(T.rchild, key)
else:
DeleteNode(T.lchild, key)
return T
def DeleteNodeFromTree(T, key):
bull, p = searchTree(T, key, None, None)
if not bull:
print("这棵树中不存在结点 %s, 删除失败"%key)
return T
else:
return DeleteNode(T, key)
总结:
保持了链表结构的插入删除不需要移动元素;
插入删除时间性能较好;
当二叉排序树是完全二叉树一样的层数时,时间复杂度O(logn);
8.7平衡二叉树(AVL树)
1.平衡二叉树:每个节点左子树和右子树的高度差小于等于1,且是一颗二叉排序树。
2.平衡因子BF(Balance Factor):左子树深度减去右子树深度,只能是-1,0,1
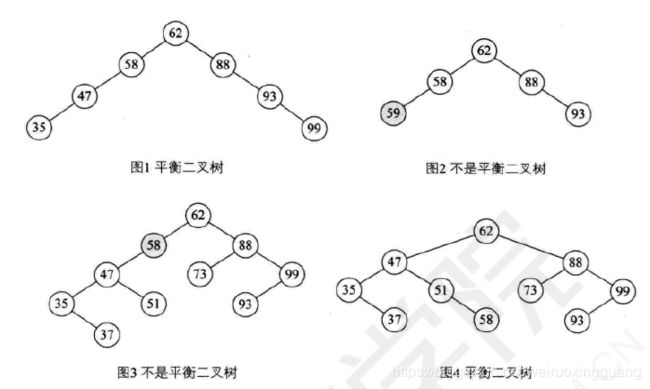
#因为图1的58这个节点,左子树是47-35,高度是1。。。右子树高度0。也就是说None和叶子节点的高度都是1。
#补充,图1是不是平衡二叉树存疑,后面又说这样的不是平衡二叉树。
3.距离插入节点最近的,且平衡因子绝对值大于1 的节点为根的子树,称为最小不平衡子树。

8.7.1平衡二叉树实现原理
1.插入:
按照二叉排序树的左小右大的规则,找到相应的叶子节点,在该节点的子节点插入新元素。
2.插入新节点后的平衡
(1)先检查是否破坏了平衡
(2)若是,则找出最小不平衡子树。进行相应的旋转,使之成为新的平衡子树。
具体操作:
最小不平衡子树根节点的平衡因子BF大于1时,右旋,小于-1时左旋。插入节点后,最小不平衡子树根节点的BF和它的子树BF符号相反时,对子树节点先进行旋转,使符号相同,在反向旋转一次。
简单的右旋:
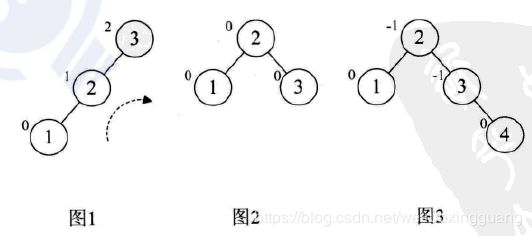
带子树的左旋:
#注意3所在子树的迁移。从4的左子树迁移到2的右子树 。
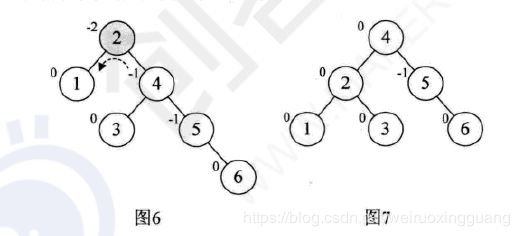
最复杂的需要先右旋,在左旋。



8.8多路查找树(B树)
数据太大时,二叉树的深度太大,需要拓宽每个节点的分支数(即degree,度)。
多路查找树(multy-way searth tree):每个节点有多个子结点,且每个节点处可以存储多个元素。
因为子节点数和每个节点存储元素的数量不同,分为2-3树,2-3-4树,B树,B+树。
2-3树/2-3-4树
略,待整理
B树
B树(B-tree),是一种平衡的多路查找树。
#B树就是B-tree,树没有什么B减树。
节点最大的孩子数称为B树的阶(Order),2-3,2-3-4树都是B树特例,分别是3阶,4阶B树。

#重点是k-1个元素和k的孩子,以及它们之间的数据大小关系。
#次重要的是,根节点和叶节点。

#B树B+树B*树
#MySQL的索引结构是B+树
B+树:节点中的元素会在子节点中再次列出,且每个叶子节点有指向下一个节点的指针。
严格意思上已经不算是树结构。
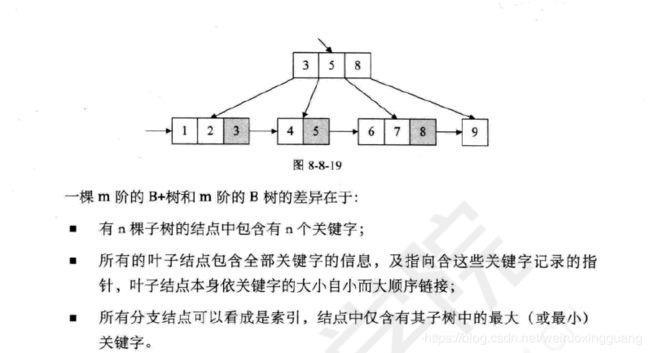
8.9散列表(哈希表)
记录的存储位置和它的关键字之间建立一个确定的对应关系,使得每个关键字key对应一个存储位置f。
这种对应关系也叫做散列函数,又称为哈希(hash)函数。对应存储空间叫散列表,或哈希表(hash table)。
#简单理解就是把[2,4,7]的每个元素放在对应位置[0,0,2,0,4,0,0,7]。然后想找元素i直接去位置i。牺牲空间降低时间的一种方式。
哈希表是一种存储方法,也是查找方法。存储需要O(n)的时间,O(n)的空间。查找需要O(1)的时间。
最适合的问题是查找与定值相等的记录。不适合一对多的问题(除非对应的是一个数组),不适合范围查找,比如寻找18-22岁的同学。
2.冲突:
如果不同的关键词key,却对应f(key1)=f(key2),就会导致冲突(Collision),称key1key2为同义词。
8.10哈希函数的构造
两个要求:
1.计算简单
2.散列地址分布均匀
8.10.1直接定址法
适用于知道关键词的分布情况,比如0-100岁。适合查找表较小且连续情况。

8.10.2数字分析法
适用于关键字维数较多,且分布较均匀。
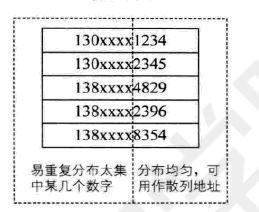
比如挑选手机号的后四位。如果冲突,对最后四位进行翻转(1234改为4321),右环位移(1234变为4123),左环位移,甚至前两位加后两位(1234变为12+34=46)。
8.10.3平方取中法
适合于不知道关键字分布,且位数不够大的情况。
比如1234,平方1522756,取中间三位227。
8.10.4折叠法
适合于不知道关键字分布,但位数较多。
将关键字分为几部分,求和,再取结果最后几位。
比如987654321,987+654+321 = 1962,后三位是962。
8.10.5除留余数法
最常用的构造方法,尽量选择接近表长的质数
f(key) = key%p,p<=m
8.10.6随机数法
f(key) = random(key)
8.11 哈希表冲突
8.11.1开放定址法
一旦发生冲突,就去寻找下一个空的地址。
线性定址法:
f(key) = (f(key)+d)MOD m,d = 1,2,3…m-1
有时候不是同义词 ,却需要争夺一个地址,称为堆积。比如在对12取余的寻址法中,如果0,1都有数字了,那48和37都在争夺2的位置。
二次探测法:双向寻找可能位置,同时增加平方运算,为了不然关键字集中在一块区域。
f(key) = (f(key)+d)MOD m,d = 12,-12,22,-22…q2,-q2,q<=m/2
随机探测法:位移量d采用随机函数计算得到。
f(key) = (f(key)+d)MOD m,d 是随机数列
8.11.2再散列函数法
准备多个散列函数,每次冲突时,更换一种散列函数计算。
8.11.3链地址法
冲突了,就在原来的位置加个链表节点。
优势一定能找到地址,缺点,冲突太多就成了链表,时间降低。
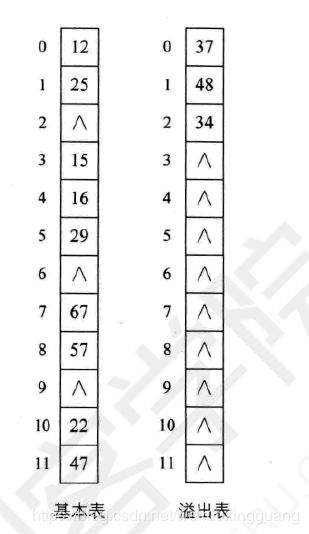
8.11.4公共溢出区法
8.12哈希表查找
没有冲突的话,时间复杂度O(1)。
实际情况下,因为冲突,时间会变长。
具体与下列因素有关:
1.哈希表是否均匀
2.处理冲突的方法
3.哈希表装填因子
装填因子是,填入表的数据/散列表长度。装填因子越大,冲突的可能越大,但也更节省空间。