AcWing 456. 车站分级 (拓扑排序)

整理的算法模板：ACM算法模板总结（分类详细版）

一条单向的铁路线上，依次有编号为1, 2, …, n 的n个火车站。

每个火车站都有一个级别，最低为1级。

现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站x，则始发站、终点站之间所有级别大于等于火车站x的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点） 

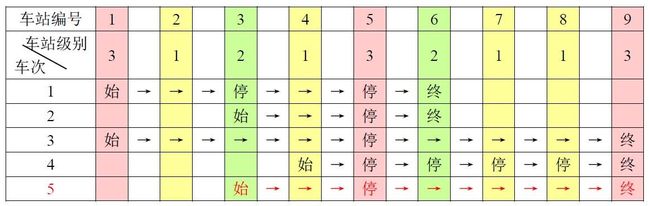
例如，下表是5趟车次的运行情况。

其中，前4趟车次均满足要求，而第5趟车次由于停靠了3号火车站（2级）却未停靠途经的6号火车站（亦为2级）而不满足要求。

 

 

现有m趟车次的运行情况（全部满足要求），试推算这n个火车站至少分为几个不同的级别。

输入格式

第一行包含 2 个正整数 n, m，用一个空格隔开。

第 i + 1 行（1 ≤ i ≤ m）中，首先是一个正整数 sisi（2 ≤ si ≤ n），表示第 i 趟车次有 sisi 个停靠站；接下来有sisi个正整数，表示所有停靠站的编号，从小到大排列。

每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

输出格式

输出只有一行，包含一个正整数，即 n 个火车站最少划分的级别数。

数据范围

1≤n,m≤10001≤n,m≤1000

输入样例：

9 3 
4 1 3 5 6 
3 3 5 6 
3 1 5 9 

输出样例：

3

 根据每趟列车的停靠点，可以在未停靠点和停靠点之间建边，如果暴力建边，空间复杂度和时间复杂度都有危险；所以有一个小技巧；

当题目中的点分为两拨，并且这两拨点之间每两个点之间都要建边的话，那么边数就是n*n；此时，只需要在中间加上虚拟源点即可，这样这个虚拟源点就像一个桥梁一样，连接着两拨点中的任意两个点；

建完图，进行拓扑排序，然后递推求每个点的最长路，然后取这些点的最大值即可；

#include 
using namespace std;
const int N=2010,M=1000010;
int h[N],e[M],ne[M],w[M],idx;
bool st[N];
int q[N+M],d[N+M],dis[N],n,m;
void add(int a,int b,int c)
{
    e[idx]=b,ne[idx]=h[a],w[idx]=c,h[a]=idx++;
}
void topsort()
{
    int hh = 0, tt = -1;

    // d[i] 存储点i的入度
    for (int i = 1; i <= n+m; i ++ )
        if (!d[i])
            q[ ++ tt] = i;

    while (hh <= tt)
    {
        int t = q[hh ++ ];

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (-- d[j] == 0)
                q[ ++ tt] = j;
        }
    }

}
int main()
{
    cin>>n>>m;
    memset(h,-1,sizeof(h));
    for(int i=1;i<=m;i++)
    {
        memset(st,0,sizeof(st));
        int t;
        cin>>t;
        int start = n, end = 1;
        while(t--)
        {
            int stop;
            cin>>stop;
            start=min(start,stop);
            end=max(end,stop);
            st[stop]=1;
        }
        int ver=n+i;
        for(int j=start;j<=end;j++)
        {
            if(!st[j]) add(j,ver,0),d[ver]++;
            else add(ver,j,1),d[j]++;
        }
    }
    topsort();
    for(int i=1;i<=n;i++) dis[i]=1;
    for(int i=0;i